Метод измерения и описание аппаратуры. Изучение эффекта Холла

Изучение эффекта Холла.

Методические указания к лабораторной работе №405.
Для студентов I, II, III курсов технических специальностей

Москва - 2002

Министерство путей сообщения Российской Федерации Московский государственный

университет путей сообщения

(МИИТ)

Кафедра «Физика-1»

Ю.Н. Харитонов, Р. М. Лагидзе, А.С. Дробат,

Утверждено редакционно- издательским советом университета

Изучение эффекта Холла.

Методические указания к лабораторной работе № 405.
Для студентов I, II, III курсов технических специальностей

Москва - 2002

РАБОТА

УДК 621.382.2

Х 20

Ю.Н. Харитонов, Р. М. Лагидзе, А.С. Дробат. Изучение эффекта Холла.

Методические указания-М.: МИИТ, 2002. - 16С..

Методические указания к выполнению лабораторной работы №405 соответствует программе и учебным планам по физике (раздел «Физика твердого тела») и предназначены для студентов I,II,III курсов технических специальностей.
Лабораторная работа поставлена при участии Е.И.Тимошкина.

ИЗУЧЕНИЕ ЭФФЕКТА ХОЛЛА.

Цель работы. Измерение холловской разности потенциалов в полупроводниковой пластине и определение концентрации, подвижности и знака носителей заряда, участвующих. в токе.

Введение

Эффект Холла заключается в возникновении поперечной разности потенциалов при пропускании тока через металлическую или полупроводниковую пластинку, помещенную в магнитное поле, направленное под некоторым углом к направлению тока. Обычно вектор индукции магнитного поля (В) направляют перпендикулярно вектору плотности тока (j).

Разность потенциалов возникает, как это показано на рис. 1, между точками A и А , лежащими на прямой, перпендикулярной как к вектору j, так и к вектору индукции В. В отсутствие магнитного поля точки A и A лежат на эквипотенциальной поверхности.

Классическая электронная теория объясняет эффект Холла следующим образом: поток электрических зарядов, попадая в магнитное поле, отклоняется от первоначального направления своего движения под действием силы Лоренца

, (1)

где q — величина заряда,

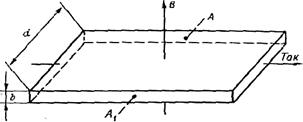
Рис. 1

—-средняя дрейфовая скорость. При этом одна из бобковых сторон пластинки получает отрицательный заряд, в то время как противоположная сторона заряжается равным ему -по величине положительным зарядом. Накопление зарядов происходит до тех пор, пока сила, действующая на электрический заряд со стороны холловского электрического поля, не уравновесит силу Лоренца:

(2)

Таким образом, напряженность поперечного холловского электрического поля

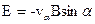
Если векторы и В взаимно перпендикулярны, то напряженность поперечного электрического поля равна по абсолютной величине ,( = 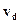), что соответствует поперечной разности потенциалов:

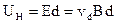(3)

(3а)

где d—расстояние (см. рис. I).

Средняя скорость направленного движения носителей тока связана с плотностью тока j соотношением j = nqν_d, где n—концентрация носителей заряда (число

носителей и единице объема, q—заряд носителя).

Следовательно,

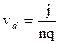(4)

Выразив плотность тока через силу тока I:

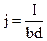
(5)

(b—толщина пластины) и подставив выражения (5) и (4) в (3), получим

(6)

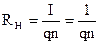(7)

Коэффициент R называют постоянной Холла.

Формула (7) получается без учета закона распределения электронов по скоростям. Более точный расчет с учетом закона распределения носителей по скоростям в рамках классической статистики приводит к выражению для постоянной Холла

(8)

Для атомных полупроводников, например, для кремния,

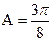
Для полупроводников с ионной связью, например

интерметаллическое соединение арсенид галлия, А= 1. В этом случае применима формула (7).

Соотношение (6) позволяет определить постоянную Холла R , м³/Кл и концентрацию носителей заряда n, м^-3, в образце из опытных данных

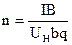; (9)

Если R известно, то, измеряя U и I, можно найти В. Этот способ измерения В используется в технике (датчики Холла).

Важной характеристикой полупроводника является подвижность в нем носителей заряда, под которой подразумевается средняя скорость, приобретаемая носителем в поле, напряженность которого равна единице. Если в поле напряженностью Е носители приобретают скорость ν, то подвижность их u, 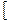м /(В·с) , равна

(10)

Используя связь между плотностью тока, напряженностью электрического поля и проводимостью j = σЕ и учитывая (4) и (10), можно выразить подвижность через проводимость и концентрацию носителей заряда:

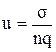(11) 6

Из соотношений (7) и (11) следует

. (12)

Таким образом, для определения подвижности носителя u необходимо измерить R и σ.

Рис. 2

Знак постоянной Холла определяется знаком носителей заряда. У полупроводников постоянная Холла может быть отрицательной и положительной, так как существует два типа проводимости. У полупроводников с электронной проводимостью (полупроводников n-типа) перемещаются электроны, и знак постоянной Холла отрицателен. У другого типа полупроводников электропроводность осуществляется положительными зарядами или так называемыми «дырками». Такие полупроводники называются дырочными (полупроводниками р-типа). Они имеют положительный знак постоянной Холла. 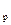При этом │q │= q = e.

Зависимость знака постоянной Холла от знака носителей заряда, создающих в данном веществе U можно понять из рис. 2, на котором демонстрируется эффект Холла для образцов с положительными и отрицательными носителями.

Направление силы Лоренца изменяется на противоположное как при изменении направления движения зарядов, так и при изменении их знака. Следовательно, при одинаковом направлении тока и магнитной индукции В сила Лоренца, действующая на положительные и отрицательные носители, имеет одинаковое направление Поэтому в случае положительных носителей потенциал верхней грани (см. рис. 2) выше, чем нижней, а в случае отрицательных носителей - ниже. Таким образом, определив знак холловской разности потенциалов, можно установить знак носителей заряда, участвующих в токе.

Метод измерения и описание аппаратуры

Изучение эффекта Холла в полупроводниках проводится на учебном приборе, общий вид и электрическая схема которого представлены соответственно на рис. 3 и 4 Исследуемый образец О (см. рис. 3), представляющий собой тонкий пластинку кремния, вмонтирован в прозрачный диэлектрический держатель D, который можно поворачи- вать на 180° с помощью рукоятки Р1 в поле постоянного магнита Цилиндрический экран Э, изготовленный из ферромагнетика, который можно перемещать с помощью рукоятки Р2, позволяет производить магнитную экранировку образца. Блок питания Б, (см. рис. 4) и включается тумблером Т, служит для создания продольного тока через образец. Величина тока регулируется потенциометром П и измеряется миллиамперметром, а его направление изменяется, с помощью переключателя П .

Рис. 3

Рис. 4

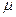Микроамперметр А с симметричной относительно нуля шкалой., включаемый последовательно с сопротивлением R или R с помощью переключателя П служит для определения тока, вызванного ЭДС Холла Все приборы и приспособления закреплены на панели, в которую вмонтированы также клеммы 1~12, с помощью которых осуществляется сборка цепи питания исследуемого образца и цепи измерения ЭДС Холла. В панели имеется окно для наблюдения за взаимным расположением магнитного экрана, исследуемого образца и постоянного „магнита, южный и северный полюса которого обозначены буквами S и N. Значения магнитной индукции поля постоянного магнита, удельной проводимости и толщины исследуемого образца, величины сопротивлений R и R . размещены на лабораторном стенде.

Электрическая схема измерительной установки размещена на панели установки.

В данной работе исследуется ЭДС Холла (поперечная разность потенциалов) и зависимости от величины протекающего по образцу продольного тока I при постоянном значении внешнего магнитного поля. Измерение ЭДС Холла проводится при различных углах между векторами В и j т.е. между направлениями магнитного поля и направлением тока через образец.

Для определения ЭДС Холла используют метод, основанный на измерении с помощью микроамперметра μA, нагружаемого на два различных сопротивления R₁ и R₂ двух токов i₁ и i₂ в холловской цепи. Расчет ЭДС Холла производится по формуле

(15)

Формула получается из решения уравнения Кирхгофа для холловской цепи

, (14)

где R —нагрузочное сопротивление (R или R );

R - контактное сопротивление;

R - сопротивление образца между холловскими электродами;

R - сопротивление микроамперметра.

Подставляя вместо R значения R₁ и R₂, получим систему двух уравнении:

;

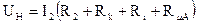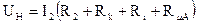. (15)

Если выбирать значения токов i₁ и i₂ достаточно близкими друг к другу, то контактное сопротивление RK можно считать постоянным при измерениях. Решая систему уравнений (15), получим расчетную формулу (13).

Для исключения паразитных ЭДС, возникающих из-за наличия асимметрии холловcких контактов и температурного градиента и образце, окончательное значение ЭДС Холла рассчитывается как среднее арифметическое из четырех измерений: двух при разном направлении продольного тока и двух при разном направлении магнитного поля.

Порядок выполнения работы

Измерсние ЭДС Холла

1. При заэкранированном исследуемом образце О включить тумблер Т, установить потенциометром П 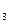максимально возможное значение продольного тока, показываемое миллиамперметром mА, и по показаниям микроамперметра 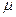А убедиться в возможном наличии паразитных ЭДС После этого продольный ток свести потенциометром П₃ до минимально возможного значения, сдвинуть рукояткой Р₂ магнитный экран Э с исследуемого образца О и тем самым подготовить образец для измерения ЭДС Холла в поле постоянного магнита.

2. Поставить переключатель П₁ в нижнее положение и установить продольный ток величиной 2 мкА. Микроамперметром измерить два значения тока в холловской цепи, включая с помощью переключателя П₂ сопротивления R₁ и R₂ ().

3. Установить переключатель П в верхнее положение и

провести измерения, указанные в п. 2 4. Рукояткой Р поворачивая образец на 180°, изменив тем самым направление магнитного поля на противоположное, провести измерения, указанные в пп. 2, 3 через каждые 300.

5. Весь процесс измерений, указанный в пп. 2—4, выполнить для значений продольного тока в 4, 6, 8 и 10 мА, т. е. для каждого значения продольного тока измеряются токи через образец, при углах 0⁰, 30⁰, 60⁰, 90⁰, 120⁰, 150⁰, 180⁰. Полученные данные занести в таблицу. Выключить тумблер Т

6. Рассчитать ЭДС Холла по формуле (13), взяв значения сопротивлений R₁ и R₂ из таблицы на приборе Тб; данные занести в таблицу.

7. Построить график U =f(I) и определить по нему среднее значение отношения U .

8. Построить график зависимости 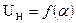для указанных значений продольного тока.

9. Вычислить значение постоянной Холла, концентрации и подвижности носителей заряда. Значение индукции магнитного поля, удельное сопротивление кремния и толщина образца указаны на приборе в таблице и лабораторном стенде.

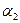
№ п/п	I, мА	I₁ _мкА	I₂ _мкА	I₃ _мкА	I₄ _мкА	I₅ _мкА	I₆ _мкА	U_Hi,В (i=1~4)	U_H=

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.В чем заключается эффект Холла?

2. Что называется подвижностью электронов и дырок и как она зависит от температуры?

3. Чему раина сила Леренца и как определить ее направление?

4. Как определить знак носителей тока при помощи эффекта Холла?

5. Укажите различные применения эффекта Холла.

6. Что такое э.д.с.?

7.Что называется эффектом Холла?

8.Работа каких сторонних сил создает холловскую э.д.с.?

9.Какую составляющую магнитного поля измеряют холловские датчики?

10.Как с помощью эффекта Холла определяется тип носителей и их концентрация?

11.Почему в датчиках Холла не используются собственные полупроводники?

12.Где больше холловская разность потенциалов: в полупроводниках или металлах, и почему?

13.Как объяснить, что в висмуте (металл) холловская постоянная имеет другой знак, чем для меди?

Список литературы

1.Савельев И. В. Курс общей физики. – М., Наука, 1987.-Т.2, §73.

2. Епифанов Г.И. Физика твердого тела.-М.: Высш. Шк., 1977.

3. Епифанов Г.И. Физические основы микроэлектроники.-М.: «Советское радио», 1971.-Гл 7 § 10.

Содержание работы

Цель работы……………………………………………3

Введение……………………………………………….3

Метод измерения и описания аппаратуры…………..8

Порядок выполнения работы……………………….12

Контрольные вопросы……………………………….15