Последовательность уравнивания сети триангуляции

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ГОСУДАРСТВЕННОЕ ВЫСШЕЕ УЧЕБНОЕ ЗАВЕДЕНИЕ

"ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ"

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ лабораторных работ

ПО ДИСЦИПЛИНЕ

"ВЫСШАЯ ГЕОДЕЗИЯ И ОСНОВЫ ФОТОГРАММЕТРИИ"

Часть 3. "Уравнивание сети триангуляции параметрическим способом"

Донецк – ДонНТУ – 2009

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ГОСУДАРСТВЕННОЕ ВЫСШЕЕ УЧЕБНОЕ ЗАВЕДЕНИЕ

"ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ"

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ лабораторных работ

ПО ДИСЦИПЛИНЕ

"ВЫСШАЯ ГЕОДЕЗИЯ И ОСНОВЫ ФОТОГРАММЕТРИИ"

Часть 3. "Уравнивание сети триангуляции параметрическим способом"

Рассмотрено:

на заседании кафедры

маркшейдерского дела

протокол № 2

от 15.10.2009 г.

Утверждено:

на заседании учебно-

издательского совета

ДонНТУ

протокол № __

От ___.___.2009 г.

Донецк – ДонНТУ – 2009

УДК 622.1: 528

Методические указания к выполнению лабораторных работ по дисциплине "Высшая геодезия и основы фотограмметрии". Часть 3. "Уравнивание сети триангуляции параметрическим способом". // В.В. Мирный, И.В. Филатова. Донецк: ДонНТУ, 2009

Методические указания предназначены для подготовки магистров, специалистов, бакалавров, которые обучаются по формам обучения: дневная, заочная, экстернат.

Методические указания к лабораторным работам по дисциплине "Высшая геодезия и основы фотограмметрии" рекомендованы к изданию методической комиссией специальности "Маркшейдерское дело" (протокол № 2 от 15.10.2009 г.)

Авторы:

В.В. Мирный, проф.

И.В. Филатова, доц.

Рецензент:

С.Б. Кулибаба, вед. науч. сотр.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ лабораторных работ

ПО ДИСЦИПЛИНЕ "ВЫСШАЯ ГЕОДЕЗИЯ И

ОСНОВЫ ФОТОГРАММЕТРИИ"

Часть 3. "Уравнивание сети триангуляции параметрическим способом"

Составители:

Вячеслав Васильевич Мирный

Ирина Викторовна Филатова

Уравнивание сети триангуляции параметрическим способом

Необходимо уравнять сеть триангуляции, которая состоит из 6 пунктов, из которых пункты Бург, Вассертурм, Вильмер – жесткие, а пункты Шанце, Эгидиус и Штейерндиб – определяемые.

Число нормальных уравнений, соответствующих данной сети, равно 22.

1. По материалам предварительной обработки составлена схема сети, которая приведена на рис. 3.1.

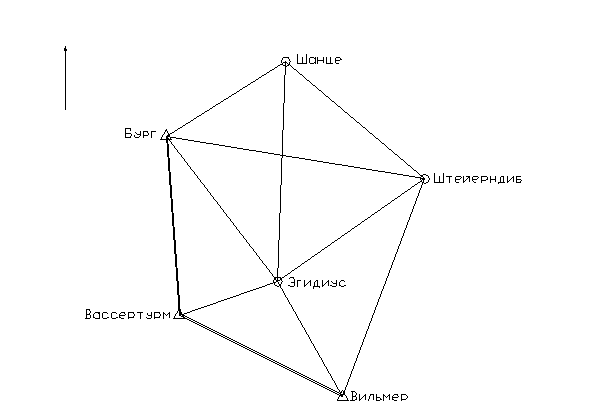
Рис. 3.1 – Схема сети триангуляции

2. Составлен список исходных данных. Координаты исходных пунктов приведены в таблице 3.1, сводка средних приведенных к центру и на плоскость направлений – в таблице 3.2.

Таблица 3.1– Координаты исходных пунктов

Название исходного пункта	Координаты, м
Х	У
Бург	-24977,399	-25842,799
Вассертурм	-29071,474	-25538,488
Вильмер	-30945,359	-21777,609

Таблица 3.2 – Сводка средних приведенных к центру и на плоскость направлений

Пункт стояния	Пункт визирования	Приведенные и редуцированные на плоскость направления
градусы	минуты	секунды
Эгидиус	Вассертурм			00,00
Бург			39,31
Шанце			26,86
Штейерндиб			52,21
Вильмер			06,68
Вассертурм	Бург			18,89
Эгидиус			00,00
Вильмер			26,74
Вильмер	Вассертурм			17,37
Эгидиус			00,00
Штейерндиб			30,53
Штейерндиб	Вильмер			43,25
Эгидиус			00,00
Бург			16,56
Шанце			34,35
Шанце	Штейерндиб			59,57
Эгидиус			00,00
Бург			01,92
Бург	Шанце			54,13
Штейерндиб			21,66
Эгидиус			00,00
Вассертурм			40,05

ПОСЛЕДОВАТЕЛЬНОСТЬ УРАВНИВАНИЯ СЕТИ ТРИАНГУЛЯЦИИ

ПАРАМЕТРИЧЕСКИМ СПОСОБОМ

2. В таблицу 3.3 записываем координаты исходных пунктов (Бург, Вассертурм и Вильмер), значения исходных координат пунктов даны по условию и приведены в таблице 3.1. Предварительно полученные координаты определяемых пунктов берем из лабораторной работы № 1 "Предварительные вычисления в триангуляции" из таблицы 1.7. Графы поправки и окончательно уравненные пункты заполняются после выполнения уравнительных вычислений.

Таблица 3.3 – Список координат

№ п/п	Названия пунктов	Приближенные координаты, м	Поправки, м	Окончательные координаты, м
Х₀	У₀	dХ	dУ	Х	У
	Бург					-24977,399	-25842,799
	Вассертурм					-29071,474	-25538,488
	Вильмер					-30945,359	-21777,609
	Шанце	-23266,8	-23087,1	0,090	0,270	-23266,710	-23086,830
	Эгидиус	-28308,4	-23271,9	-0,031	0,095	-28308,431	-23271,805
	Штейерндиб	-25952,1	-19888,6	0,164	-0,064	-25951,936	-19888,664

2. В таблице 3.4 приведены жесткие дирекционные углы стороны, которые были вычислены в лабораторной работе № 1 ("Предварительные вычисления в триангуляции") в таблице 1.3.

Таблица 3.4 – Исходные (жесткие) дирекционные углы

Названия сторон	Дирекционные углы a	Стороны S, м
град	мин	сек
Бург – Вассертурм			56,56	4105,369
Вассертурм – Вильмер			06,40	4201,861

Предварительные дирекционные углы вычисляем по приближенным координатам определяемых пунктов и данным координатам исходных пунктов. Вычисления предварительных дирекционных углов и длин сторон приведены в таблице 3.5. Дирекционные углы находим по формулам:

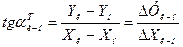
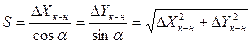
где Х_н,У_н – координаты начального пункта;

Х_к,У_к – координаты конечного пункта;

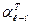– табличное значение дирекционного угла.

Таблица 3.5 – Вычисление приближенных дирекционных углов направлений и длин сторон

Сторона н-к	Х_К, м Х_Н, м DХ=Х_К–Х_Н, м DХ+DУ, м	У_К, м У_Н, м DУ=У_К-У_Н, м DХ-DУ, м	tga^Т a^Т a	S_К-Н, м
Эгидиус – Вассертурм	-29071,474	-25538,488	2,9703384	2391,6
-28308,4	-23271,9	71⁰ 23' 36",88	2391,6
-763,074	-2266,588	251⁰ 23' 36",88
Эгидиус – Бург	-24977,399	-25842,799	-0,7718097	4207,7
-28308,4	-23271,9	37⁰ 39' 40", 71	4207,7
3331,001	-2570,899	322⁰ 20' 19", 29
Эгидиус – Шанце	-23266,8	-23087,1	0,0366550	5045,0
-28308,4	-23271,9	2⁰ 05' 57",26	5045,0
5041,600	184,800	2⁰ 05' 57",26
Эгидиус – Штейерндиб	-25952,1	-19888,6	1,4358528	4123,0
-28308,4	-23271,9	55⁰08' 40",95	4123,0
2356,300	3383,300	55⁰08' 40",95
Эгидиус – Вильмер	-30945,359	-21777,609	-0,5666721	3030,9
-28308,4	-23271,9	29⁰ 32' 20",46	3030,9
-2636,959	1494,291	150⁰ 27' 39",54

Продолжение табл.3.5

Сторона н – к	Х_К, м Х_Н, м DХ=Х_К–Х_Н, м DХ+DУ, м	У_К, м У_Н, м DУ=У_К-У_Н, м DХ-DУ, м	tga^Т a^Т a	S_К-Н, м
Вильмер – Штейерндиб	-25952,1	-19888,6	0,3783118	5338,6
-30945,359	-21777,609	20⁰43' 20",00	5338,6
4993,259	1889,009	20⁰43' 20",00
Штейерндиб – Бург	-24977,399	-25842,799	-6,1087441	6033,5
-25952,1	-19888,6	80⁰42' 11",35	6033,5
974,701	-5954,199	279⁰17' 48",65
Штейерндиб – Шанце	-23266,8	-23087,1	-1,1911146	4176,3
-25952,1	-19888,6	49⁰ 59' 05",53	4176,3
2685,300	-3198,500	310⁰00' 54",47
Шанце – Бург	-24977,399	-25842,799	1,6109556	3243,0
-23266,8	-23087,1	58⁰ 10' 12",27	3243,6
-1710,599	-2755,699	238⁰ 10' 12",27

При вычислении приближенных дирекционных углов и длин сторон жесткие координаты данных точек не подвергаются округлению, поэтому они берутся такими, какими даны в таблице исходных данных (см. табл. 3.3)

Следует заметить, что вычисления дирекционных углов и длин сторон необходимо производить очень тщательно так, как допущенные ошибки будут обнаружены только в конце уравнительных вычислений.

3. Вычисление свободных членов уравнений погрешностей приведено в таблице 3.6. По каждому направлению вычисляются ориентирные углы:

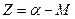где Z – ориентирный угол;

a – дирекционный угол;

М – измеренное направление.

На каждом пункте после вычисления ориентирного угла вычисляется среднее значение ориентирного угла Z₀, которое является предварительным (приближенным) значением ориентирного угла на данном пункте. После этого вычисляем приближенно ориентированные направления:

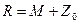где Z₀ – среднее значение ориентирного угла.

Свободные члены уравнений погрешностей:

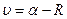Контроль. Сумма свободных членов на каждом пункте должна быть равна нулю.

В таблице 3.6 приведено вычисление коэффициентов уравнений погрешностей, которые определяются по формуле:

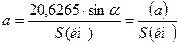
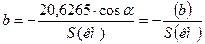Знаки коэффициентов (a) и (b) определяются в соответствии с величиной дирекционного угла данного направления по таблице 3.7.

Таблица 3.7 – Определение знаков коэффициентов

Значение дирекционного угла	Знаки коэффициентов
a	b
0 – 90	+	–
90 – 180	+	+
180 – 270	–	+
270 – 360	–	–

Таблица 3.6 – Вычисление коэффициентов и свободных членов уравнений погрешностей

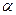
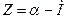
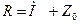
Название направлений	Измеренные направления М	Дирекционные углы (жесткие и приближенные)	Ориентирные углы	Приближенно ориентированные направления	Свободный член	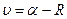Расстояние S, км
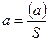
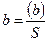
град	мин	сек	град	мин	сек	град	мин	сек	град	мин	сек
				Эгидиус
Вассертурм			00,00			36,88			36,88			38,04	-0,89	2,392	-19,55	6,58	-8,17	2,75
Бург			39,31			19,29			39,98			17,35	2,21	4,208	-12,60	-16,33	-2,99	-3,88
Шанце			26,86			57,26			30,40			4,63	-7,37	5,045	0,76	-20,61	0,15	-4,09
Штейерндиб			52,21			40,95			48,74			30,25	10,97	4,123	16,93	-11,79	4,11	-2,86
Вильмер			6,68			39,54			32,86			44,72	-4,91	3,031	10,17	17,95	3,36	5,92
Среднее									37,77				0,00

				Вассертурм
Бург			18,89			56,56			37,67			56,96	-0,40	4,105	-1,53	-20,57	-0,37	-5,01
Эгидиус			00,00			36,88			36,88			38,07	-1,19	2,392	19,55	-6,58	8,17	-2,75
Вильмер			26,74			6,40			39,66			4,81	1,59	4,202	18,46	9,20	4,39	2,19
Среднее									38,07				0,00

				Вильмер
Вассертурм			17,37			6,40			49,03			3,38	3,02	4,202	-18,46	-9,20	-4,39	-2,19
Эгидиус			00,00			39,54			39,54			46,01	-6,47	3,031	-10,17	-17,95	-3,36	-5,92
Штейерндиб			30,53			20,00			49,47			16,54	3,46	5,339	7,30	-19,29	1,37	-3,61
Среднее									46,01				0,01

Продолжение табл. 3.6

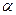
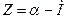
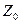
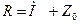
Название направлений	Измеренные направления М	Дирекционные углы (жесткие и приближенные)	Ориентирные углы	Приближенно ориентированные направления	Свободный член	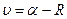Расстояние S, км
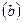
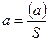
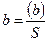
град	мин	сек	град	мин	сек	град	мин	сек	град	мин	сек
				Штейерндиб
Вильмер			43,25			20,00			36,75			15,73	4,27	5,339	-7,30	19,29	-1,37	3,61
Эгидиус			0,00			40,95			40,95			32,48	8,47	4,123	-16,93	11,79	-4,11	2,86
Бург			16,56			48,65			32,09			49,04	-0,39	6,034	-20,36	-3,33	-3,37	-0,55
Шанце			34,35			54,47			20,12			06,83	-12,36	4,176	-15,80	-13,26	-3,78	-3,18
Среднее									32,48				0,00

				Шанце
Штейерндиб			59,57			54,47			54,90			00,41	-5,94	4,176	15,80	13,26	3,78	3,18
Эгидиус			0,00			57,26			57,26			00,84	-3,58	5,045	-0,76	20,61	-0,15	4,09
Бург			1,92			12,27			10,35			02,76	9,51	3,244	-17,52	10,88	-5,40	3,35
Среднее									0,84				-0,01

				Бург
Шанце			54,13			12,27			18,14			14,36	-2,09	3,244	17,52	-10,88	5,40	-3,35
Штейерндиб			21,66			48,65			26,99			41,89	6,76	6,034	20,36	3,33	3,37	0,55
Эгидиус			0,00			19,29			19,29			20,23	-0,94	4,208	12,60	16,33	2,99	3,88
Вассертурм			40,05			56,56			16,51			00,28	-3,72	4,105	1,53	20,57	0,37	5,01
Среднее									20,23				0,00

4. Начальные уравнения поправок составляются для каждого измеренного направления и записываются в таблицу 3.8. В работе встречаются все 4 вида начальных уравнений:

a. Начальная к и конечная i точки измеренного направления определяемые (направления Шанце – Эгидиус, Эгидиус – Штейерндиб) уравнение имеет вид:

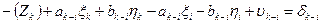
b. Начальная точка к измеренного направления определяемая точка, а конечная точка i этого направления жесткая и уравнение имеет вид (направления Эгидиус – Вильмер, Эгидиус – Вассертурм, Эгидиус – Бург, Шанце – Бург, Штейерндиб – Вильмер):

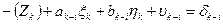
Такой вид уравнения обусловлен тем, что поправки в координаты жесткой точки i равны нулю, так как 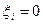и .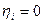

c. Начальная точка к измеренного направления жесткая точка, а конечная точка i этого направления определяемая и уравнение имеет вид (направления, обратные направлениям, описанным в предыдущем пункте, это направления (Вильмер – Эгидиус, Вассертурм – Эгидиус, Бург – Эгидиус, Бург – Шанце, Вильмер – Штейерндиб):

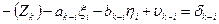
В этом случае 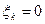и .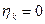

d. Начальная точка к измеренного направления и конечная точка i этого направления жесткие (направления Бург – Вассертурм, Вассертурм – Вильмер и обратные им). Уравнение имеет вид:

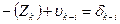
Так как 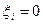, , 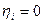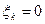и .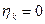

В данных формулах:

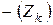
	–	неизвестное
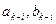
	–	коэффициенты уравнений поправок
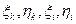
	–	поправки к предварительным координатам определяемых пунктов;
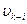
	–	свободный член
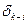
	–	поправка

Количество нормальных уравнений должно быть равным количеству измеренных направлений. Для нашего случая: измеренных направлений 22 и количество уравнений – 22 Составленные для рассматриваемой сети уравнения приведены в табл. 3.8.

Уравнения (см. табл. 3.8), с подставленными числовыми значениями коэффициентов и свободных членов, приведены в таблице 3.9.

Таблица 3.8 – Уравнения поправок (в общем виде)

Пункт	Направления	№ уравнения поправок	Уравнение поправок	Число измеренных направлений на станции
Эгидиус	Вассертурм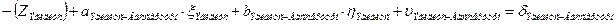
Бург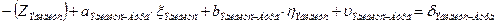
Шанце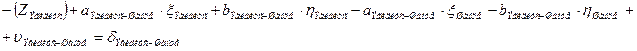
Штейерндиб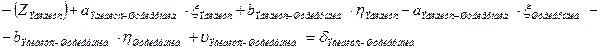
Вильмер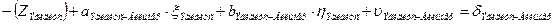
Вассертурм	Бург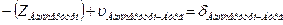
Эгидиус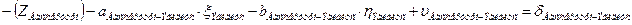
Вильмер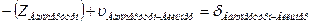
Вильмер	Вассертурм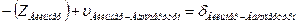
Эгидиус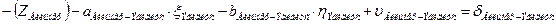
Штейерндиб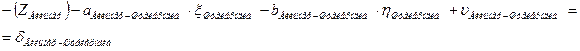

Продолжение табл. 3.8

Пункт	Направления	№ уравнения поправок	Уравнение поправок	Число измеренных направлений на станции
Штейерндиб	Вильмер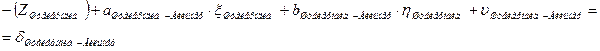
Эгидиус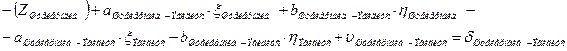
Бург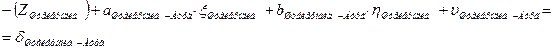
Шанце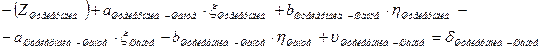
Шанце	Штейерндиб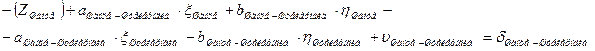
Эгидиус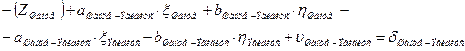
Бург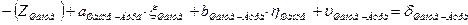
Бург	Шанце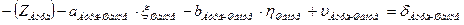
Штейерндиб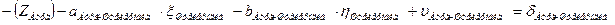
Эгидиус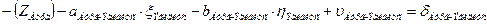
Вассертурм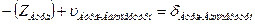
Всего измеренных направлений

Таблица 3.9 – Уравнения поправок (с подставленными значениями)

Пункт	Направления	№ уравнения поправок	Уравнение поправок (с подставленными значениями)	Число измеренных направлений на станции
Эгидиус	Вассертурм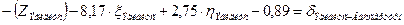
Бург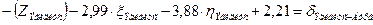
Шанце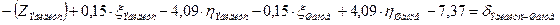
Штейерндиб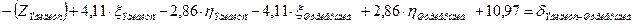
Вильмер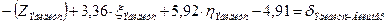
Вассертурм	Бург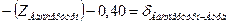
Эгидиус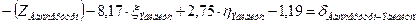
Вильмер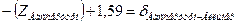
Вильмер	Вассертурм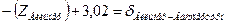
Эгидиус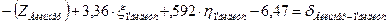
Штейерндиб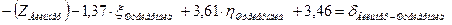
Штейерндиб	Вильмер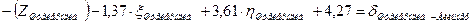
Эгидиус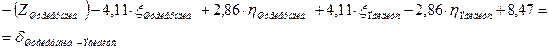
Бург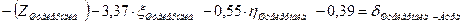
Шанце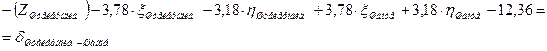

Продолжение табл. 3.9

Пункт	Направления	№ уравнения поправок	Уравнение поправок (с подставленными значениями)	Число измеренных направлений на станции
Шанце	Штейерндиб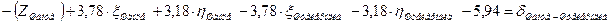
Эгидиус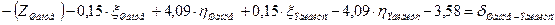
Бург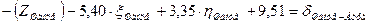
Бург	Шанце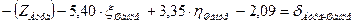
Штейерндиб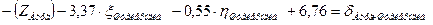
Эгидиус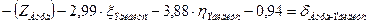
Вассертурм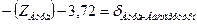
Всего измеренных направлений

Таблица 3.10 – Вычисление коэффициентов нормальных уравнений

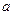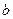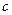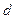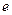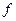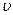
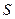
№ уравнений поправок	x_{Эгидиус}	h_{Эгидиус}	x_Шанце	h_Шанце	x_{Штейерндиб}	h_{Штейерндиб}			P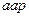
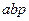
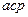
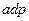
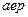
	-8,17	2,75	0,00	0,00	0,00	0,00	-0,89	-6,31		66,749	-22,468	0,000	0,000	0,000
	-2,99	-3,88	0,00	0,00	0,00	0,00	2,21	-4,66		8,940	11,601	0,000	0,000	0,000
	0,15	-4,09	-0,15	4,09	0,00	0,00	-7,37	-7,37		0,023	-0,614	-0,023	0,614	0,000
	4,11	-2,89	0,00	0,00	-4,11	2,86	10,97	10,94		16,892	-11,878	0,000	0,000	-16,892
	3,36	5,92	0,00	0,00	0,00	0,00	-4,91	4,37		11,290	19,891	0,000	0,000	0,000
å	-3,54	-2,19	-0,15	4,09	-4,11	2,86	0,01	-3,03		-2,506	-1,551	-0,106	2,896	-2,910
å по строке								-3,03	-0,200
	0,00	0,00	0,00	0,00	0,00	0,00	-0,40	-0,40		0,000	0,000	0,000	0,000	0,000
	-8,17	2,75	0,00	0,00	0,00	0,00	-1,19	-6,61		66,749	-22,468	0,000	0,000	0,000
	0,00	0,00	0,00	0,00	0,00	0,00	1,59	1,59		0,000	0,000	0,000	0,000	0,000
å	-8,17	2,75	0,00	0,00	0,00	0,00	0,00	-5,42		-22,250	7,489	0,000	0,000	0,000
å по строке							-5,42	-0,333
	0,00	0,00	0,00	0,00	0,00	0,00	3,02	3,02		0,000	0,000	0,000	0,000	0,000
	3,36	5,92	0,00	0,00	0,00	0,00	-6,47	2,81		11,290	19,891	0,000	0,000	0,000
	0,00	0,00	0,00	0,00	-1,37	3,61	3,46	5,70		0,000	0,000	0,000	0,000	0,000
å	3,36	5,92	0,00	0,00	-1,37	3,61	0,01	11,53		-3,763	-6,630	0,000	0,000	1,534
å по строке							11,53	-0,333
	0,00	0,00	0,00	0,00	-1,37	3,61	4,27	6,51		0,000	0,000	0,000	0,000	0,000
	4,11	-2,86	0,00	0,00	-4,11	2,86	8,47	8,47		16,892	-11,755	0,000	0,000	-16,892
	0,00	0,00	0,00	0,00	-3,37	-0,55	-0,39	-4,31		0,000	0,000	0,000	0,000	0,000
	0,00	0,00	3,78	3,18	-3,78	-3,18	-12,36	-12,36		0,000	0,000	0,000	0,000	0,000
å	4,11	-2,86	3,78	3,18	-12,63	2,74	-0,01	-1,69		-4,223	2,939	-3,884	-3,267	12,977
å по строке							-1,69	-0,250
	0,00	0,00	3,78	3,18	-3,78	-3,18	-5,94	-5,94		0,000	0,000	0,000	0,000	0,000
	0,00	0,00	-0,15	4,09	0,15	-4,09	-3,58	-3,58		0,000	0,000	0,000	0,000	0,000
	0,00	0,00	-5,40	3,35	0,00	0,00	9,51	7,46		0,000	0,000	0,000	0,000	0,000
å	0,00	0,00	-1,77	10,62	-3,63	-7,27	-0,01	-2,06		0,000	0,000	0,000	0,000	0,000
å по строке							-2,06	-0,333
	0,00	0,00	-5,40	3,35	0,00	0,00	-2,09	-4,14		0,000	0,000	0,000	0,000	0,000
	0,00	0,00	0,00	0,00	-3,37	-0,55	6,76	2,84		0,000	0,000	0,000	0,000	0,000
	-2,99	-3,88	0,00	0,00	0,00	0,00	-0,94	-7,81		8,940	11,601	0,000	0,000	0,000
	0,00	0,00	0,00	0,00	0,00	0,00	-3,72	-3,72		0,000	0,000	0,000	0,000	0,000
å	-2,99	-3,88	-5,40	3,35	-3,37	-0,55	0,01	-12,83		-2,235	-2,900	-4,037	2,504	-2,519
å по строке							-12,83	-0,250
									172,787	-6,850	-8,049	2,746	-24,701
									Контроль

Продолжение табл. 3.10

<== предыдущая лекция	\|	следующая лекция ==>
Робота №7 визначення властивостей пластмас	\|	Асқынбаған тісжегіні емдеу

Поделиться с друзьями:

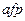
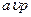
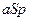
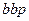
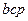
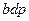
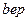
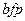
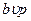
Дата добавления: 2015-10-27; Мы поможем в написании ваших работ!; просмотров: 1176 | Нарушение авторских прав

Поиск на сайте:

Лучшие изречения:

2338 -

| 2092 -