Послідовність 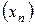 називається фундаментальною, якщо
називається фундаментальною, якщо
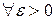
 :
: 



Теорема 1. (Критерій Коші)
Послідовність 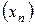 дійсних чисел збігається тоді і тільки тоді, коли вона фундаментальна.
дійсних чисел збігається тоді і тільки тоді, коли вона фундаментальна.
Доведення. Необхідність. Нехай існує  . Тоді
. Тоді 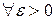
 :
: 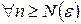 :
:
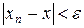


 .
.
Необхідність доведена.
Достатність. Якщо 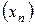 – фундаментальна, то вона обмежена, що випливає з раніше доведених тверджень. За теоремою Больцано-Вейєрштрасса існує збіжна підпослідовність
– фундаментальна, то вона обмежена, що випливає з раніше доведених тверджень. За теоремою Больцано-Вейєрштрасса існує збіжна підпослідовність  . Із означення фундаментальності
. Із означення фундаментальності 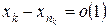

 , а далі за теоремою про суму двох збіжних послідовностей, одержимо, що
, а далі за теоремою про суму двох збіжних послідовностей, одержимо, що  збігається.
збігається.
Достатність доведена.
Теорема доведена.
Послідовність 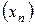 має обмежену варіацію, якщо
має обмежену варіацію, якщо 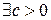
 :
:  .
.
Лема 1. (Про послідовність з обмеженою варіацією)
Послідовність 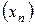 , що має обмежену варіацію – збіжна.
, що має обмежену варіацію – збіжна.
Доведення. Позначимо  , вона обмежена та неспадна, з чого слідує, що вона збіжна, і за критерієм Коші – фундаментальна
, вона обмежена та неспадна, з чого слідує, що вона збіжна, і за критерієм Коші – фундаментальна 
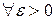

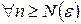











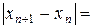
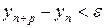

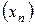 – фундаментальна
– фундаментальна  збіжна.
збіжна.
Лема доведена.
Нехай 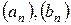 – числові послідовності. Якщо
– числові послідовності. Якщо 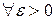

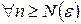
 , то будемо записувати
, то будемо записувати  та казати, що послідовність
та казати, що послідовність  є малою в порівнянні з послідовністю
є малою в порівнянні з послідовністю  .
.
Лема 2. (Критерій о-малості послідовності)

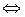
 .
.
Доведення. 
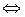
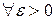

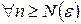


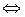
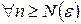
 .
.
Лема доведена.
Теорема 2. (Часткові суми о-малої послідовності)
Нехай 
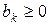 ,
,  при
при  і
і  . Тоді
. Тоді
 .
.
Доведення. З умови  ми маємо, що
ми маємо, що 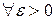

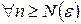



 . Крім того з умови
. Крім того з умови 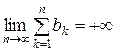 випливає, що
випливає, що  :
: 






 .
.
Теорема доведена.
Наслідок 1. (Границя відношення часткових сум)
Нехай 
 і
і 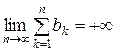 . Якщо
. Якщо  , то
, то  .
.
Доведення. Нехай  . Оскільки
. Оскільки 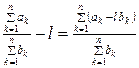 , і
, і  , то за теоремою 2 права частина прямує до нуля.
, то за теоремою 2 права частина прямує до нуля.
Якщо  , то
, то 

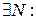




 за теоремою 2
за теоремою 2 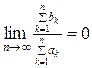

 . Аналогічно для випадку
. Аналогічно для випадку  .
.
Теорема доведена.
Наслідок 2. (теорема Коші)
Якщо існує  , то існує
, то існує  .
.
Доведення. Для доведення достатньо в останньому наслідку покласти  .
.
Теорема доведена.
Теорема 3. (Штольца)
Якщо послідовність  монотонно прямує до
монотонно прямує до  , та
, та  , то
, то  .
.
Доведення. Для доведення достатньо в наслідку покласти  ,
, 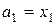 ;
; 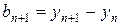 ,
,  . Тоді
. Тоді  ,
, 
 .
.
Теорема доведена.
Приклад 1. Знайти  .
.
 ;
; 

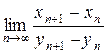
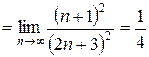

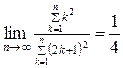 .
.
Для довільних додатних дійсних чисел  визначимо:
визначимо:
середнє арифметичне –  ;
;
середнє геометричне –  ;
;
середнє гармонічне – 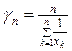 ;
;
середнє степеневе порядку  –
–  .
.
З’ясувати, яким значенням параметру  відповідають визначені вище середні, а також узагальнити середні степеневі на випадок довільного
відповідають визначені вище середні, а також узагальнити середні степеневі на випадок довільного  залишаємо читачам.
залишаємо читачам.
Приклад 2. Границя середніх – арифметичного, гармонічного, геометричного.
Нехай послідовність додатних дійсних  чисел така, що
чисел така, що  . Довести тоді, що до тієї ж самої границі збігаються також середнє арифметичне
. Довести тоді, що до тієї ж самої границі збігаються також середнє арифметичне  , середнє геометричне
, середнє геометричне  і середнє гармонічне
і середнє гармонічне  чисел
чисел  .
.
Твердження для середнього арифметичного безпосередньо випливає з теореми Коші. Для середнього гармонічного також з цієї теореми легко одержати, що  , тому що
, тому що  , з чого маємо:
, з чого маємо: 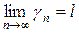 . Для середнього геометричного все випливає з теореми про двох поліцаїв та нерівності між середніми:
. Для середнього геометричного все випливає з теореми про двох поліцаїв та нерівності між середніми:  , а тому і
, а тому і  .
.
Теорема 4. (Границя кореня n-го степеня)
Якщо для послідовності додатних чисел 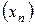
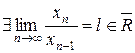 , то
, то
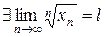 .
.
Доведення. За останнім прикладом (для середнього геометричного) маємо:
 .
.
Теорема доведена.






