Використання кореляційно-регресійного аналізу в юридичних дослідженнях

При визначенні конкретних залежностей одні показники розглядаються як фактори впливу (ознаки), що обумовлюють зміни іншого показника (ре­зуль­тативного фактора). Функціональні зв’язки характеризуються повною відповідністю між змінами факторної ознаки змінами результативної вели­чи­ни, причому кожному значенню фактора-ознаки відповідає певне значення результативного фактора. При кореляційних зв’язках між змінами факторів-ознак та результативного показник повної відповідності не існує.

Вплив окремих факторі виявляється лише в середньому при значній кіль­кості спостережень фактичних даних. Крім того, фактор-ознака, як правило, залежить від зміни інших показників.

Форма взаємозв’язку випадкових величин і функції дістала назву рів­ня­ння регресії. Виділяють парну (просту) та множинну регресії лінійного і нелінійного (квадратичного, експоненціального, напівлогарифмічного типів. Вид, а також параметри рівняння регресії знаходять за допомогою методу найменших квадратів. За наявності кореляційної залежності визначають лише тенденцію зміни результативного показника при зміна факторів-ознак.

Найчастіше застосовуються такі математичні залежності для оцінювання кореляційного зв’язку між факторами:

- прямолінійна: у = а₀ +а₁х, де а₀ – стала (область існування моделі); а – коефіцієнт регресії, що характеризує середню зміну результативного показника при змінах фактора-ознаки;

- параболічна: у = а₀+а₁х +а₂х²;

- показникова: у = а₀+а₁^х;

- степенева: y=a₀х^а1;

- гіперболічна: у=а₀+ ;

- напівлогарифмічна: у =а₀+а₁lgx.

Статистичне оцінювання тісноти зв’язку ґрунтується на показниках варіації:

- загальній дисперсії s_у² результативного показника, обумовленій впли­вом усіх факторів у сукупності;

- факторній дисперсії s_ух² результативного показни­ка, що показує його варіацію під впливом окремих фак­торів;

- залишковій дисперсії s_S² результативного показни­ка, яка показує його варіацію під впливом усіх факто­рів, крім виділеного, причому

Якісною оцінкою ступеня зв’язку випадкових вели­чин постає коефіцієнт детермінації, що визначається виразом R² = відношенням факторної та загальної дисперсій. Індекс кореляції розраховується як квад­ратний корінь із коефіцієнта детермінації, тобто r = , причому його значення лежать у межах від –1 до +1 (знак "мінус" указує на наявність зворотного зв’язку між факторами).

Для оцінювання значущості індексу кореляції мож­на використовувати F’‑критерій Фішера.

де п – число значень у масиві; т – число параметрів рівняння регресії (факторів). Фактичне значення цього критерію порівнюють із критичним зна­ченням, яке визначають з урахуванням рівня значущості та кількості ступенів вільності. Якщо фактичне значення F-критерію Фішера більше від кри­тич­ного, то індекс кореляції R вважається істотним.

Якісне оцінювання ступеня зв’язку випадкових ве­личин може бути вико­на­не з використанням коефіцієн­та кореляції за шкалою Чеддока:

0,1...0,3 – незначний; 0,7... 0,9 – високий;

0,3...0,5 – помірний; 0,9... 0,99 – дуже високий;

0,5... 0,7 – істотний; 1,0 – функціональний.

Якщо коефіцієнт кореляції r > 0,7, то варіація залежної змінної переважно обумовлена впливом факторів, і для прогнозування можна використовувати одержані регресійні моделі.

Якщо аналізується невелика сукупність даних (п < < 30), то для визначення їх довірчого інтервалу використовується t-критерій Стьюдента. Розраховане значення t-критерію t для коефіцієнта кореляції порів­ню­ється з критичним з урахуванням прийнятого рівня значущості, а також кількості ступенів вільності та вважається типовим, якщо tp > t_к. Аналогічне оцінюється значущість факторів х на основі t-критерій:

параметрів моделі ;

Табличний редактор Excel дає змогу використати різні інструменти Ана­лиза данных (Корреляция, Ковариация, Регрессия) для одержання пара­метрів ліній­ної парної та множинної регресій, а також оцінки ступе­ня зв’язку.

Аналіз правових даних є досить складною задачею, тому під час про­ве­дення кореляційно-регресійного аналізу слід дотримуватись таких вимог до вхід­них даних для одержання вірогідного результату:

q статистична сукупність даних має включати дос­татню кількість спо­стережень або однорідних об’єктів (не менше п’яти) – чим більша кількість спостере­жень, тим точнішими будуть результати одержаних рівнянь залежності;

q статистичні дані мають бути відібрані за однакові періоди часу (місяць, квартал, рік) або для однорідних об’єктів;

q при проведенні множинної регресії кількість фак­торів має бути мен­шою (хоча б на два), ніж кількість спостережень.

Розглянемо процедуру проведення багатофакторного кореляційного ана­лі­зу із застосуванням засобу Анализ данных Excel.

Етап 1. Визначаємо фактори, що впливають на результативний показник, і відбираємо найістотніші них. Основні правила відбору факторів:

- результативним фактором, як правило, визначається якісний показник ефективності певної сфери діяльності підприємства (прибуток, рента­бель­ність, дохідність, обсяг реалізації, собівартість тощо);

- слід ураховувати наявність причинно-наслідкового зв’язку між показ­ни­ками, що дає змогу розкрити сутність явищ, які досліджуються;

- необхідно відбирати найбільш значущі фактори, оскільки охопити всі умови та обставини впливу на результативний показник неможливо;

- всі фактори мають бути кількісними з одиницями виміру;

- не рекомендується включати в кореляційну модель взаємопов’язані фактори, для чого їх слід перевірити на мультиколінеарність;

- не можна включати в кореляційну модель фактори, зв’язок яких з ре­зуль­тативним показником має функціональний характер.

Перевірка на мультиколінеарність передбачає оцінювання взаємозв’язку між окремими факторами-ознаками. За наявності лінійної залежності між факторами система лінійних рівнянь не матиме однозначною розв’язку, вна­слі­док чого коефіцієнти регресії та інші оцінки будуть нестійкими. Крім того наявність взаємозв’язку факторів ускладнює економічну інтерпретацію рів­ня­ння зв’язку, оскільки зміна одного фактора спричиняє, як правило, зміну іншого, який з ним пов’язаний.

Існує кілька методів виключення мультиколінеарності, проте найчастіше застосовується метод оцінювання парних коефіцієнтів кореляції. Критерієм мультиколінеарності вважається виконання двох нерівностей:

r_xjy >r_xjxk; r_xky>r_xjxk

Якщо ці нерівності або хоча б одна з них не виконується, то виключається той фактор х, зв’язок якого результативним показником у буде менш тісним.

Для оцінювання парного кореляційного зв’язку між факторами можна вико­ристати інструмент Корреляция з Анализа данных або статистичну функцію КОРРЕЛ. У першому випадку дістанемо таблицю парних коефі­ці­єнтів кореляції для кількох факторів одночасно (але без зворотного зв’язку з вхідними даними), у другому випадку можемо виконати обчислення лише для двох масивів.

Розглянемо спочатку процедуру застосування інструмента Корреляция. Показники, відібрані для про ведення аналізу, оформляємо у вигляді таблиці-списку, дані якої можуть бути розміщені по рядкам або ж стовпцям; першим рядком (стовпцем) списку є рядок назв показників. Після подачі команди Анализ данних.../Корреляция з меню Сервис на екрані монітора з’явиться діалогове вікно, в якому потрібно вказати такі параметри:

- вхідний інтервал – посилання на діапазон аналізо­ваних даних;

- групування – визначення послідовності розміщен­ня даних (по рядках або по стовпцях);

- мітки – параметр для автоматичного формування рядка (стовпця) назв показників;

- вихідний діапазон – посилання на ліву верхню клітинку вихідного діа­па­зону активного робочого лист­ка, нового робочого листка або нової робочої книги. При цьому можна задати ім’я нового робочого листка, де ви­хідний діапазон почнеться з клітинки А1.

- множина регресії включатиме аналіз впливу трьох факторів – виро­біт­ку одного робітника, матеріаловіддачі та витрат на 1 грн. реалізації.

Одержати парні коефіцієнти кореляції можна також за допомогою ста­тистичної функції КОРРЕЛ. Для цього поетапно розраховуємо кожну пару коефіцієнтів, при копіюванні формули фіксуємо посилання на адреси пер­шо­го масиву відповідної пари (абсолютна адресація) В результаті отримаємо таку матрицю коефіцієнтів:

уу ух₁ ух₂..... ух _т

ух₁ х₁х₁ х₁х₂ ..... х₁х _т

ух₂ х₂х₁ х₂х₂ ..... х₂х _т

..........................

ух _т х₁х _т х₂х _т .... х _т х _т

Етап 2. Будуємо рівняння множинної регресії та оцінюємо одержані результати. Для виконання цього етапу можна використати інструмент Ре­грессия або статистичні функції.

Для роботи з інструментом Регрессия вхідні дані треба розмістити з дотриманням таких вимог:

- масиви даних розміщуються у стовпцях;

- перший рядок – назви показників;

- перший стовпець даних – масив у (результативний фактор), інші не­ро­зірвані масиви х – масиви факторів-ознак.

Лінійний регресійний аналіз полягає у виборі графі­ка для відображення спостережень за допомогою методу найменших квадратів. Регресія вико­ри­сто­вується для аналізу впливу на залежну змінну значень однієї або більше незалежних змінних-факторів.

Параметрами діалогового вікна Регрессия є (рис.6.3):

- вхідний інтервал Y – посилання на діапазон ре­зультативного показника. Діапазон має складатися з одного стовпця;

- вхідний інтервал Х – посилання на діапазон фак­торів-ознак. Макси­маль­не число вхідних показників дорівнює 16;

- мітки – параметр для автоматичного формування назв показників;

Рис. 6.3. Діалогове вікно команди Регрессия

- рівень надійності – дає змогу включити у вихід­ний діапазон рівень надійності до 95 %, що вводиться за замовчуванням;

- константа-нуль – прапорець, який вказує, що лі­нія регресії проходить через початок координат;

- вихідний діапазон – посилання на ліву верхню клітинку вихідного діа­па­зону активного робочого лист­ка, нового робочого листка або нової робочої книги. При цьому можна задати ім’я нового робочого листка, де ви­хідний діапазон почнеться з клітинки А1;

- залишки – дає змогу включити залишки у вихід­ний діапазон;

- стандартизовані залишки – дає можливість вклю­чити стандартизовані залишки у вихідний діапазон;

- графік залишків – діаграма залишків для кожної незалежної змінної;

- графік підбору – діаграма даних, що спостеріга­ються, а також про­гно­зо­ваних значень для кожної неза­лежної змінної;

- графік нормальної імовірності – діаграма нормальної імовірності.

У результаті виконання зазначених команд автома­тично буде побудовано таблиці регресійного аналізу (рис. 6.4):

Таблиця Регрессионная статистика включає такі показники для оціню­ва­ння адекватності моделі:

- коефіцієнт детермінації R²;

- індекс кореляції R;

- значення коефіцієнта детермінації при збільшенні кількості спо­сте­ре­жень (нормоване);

- стандартну помилку;

- кількість спостережень.

 

 

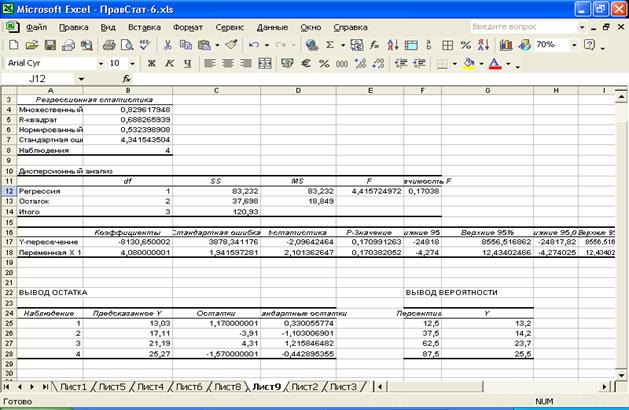
Рис. 6.4. Таблиці регресійного аналізу

Таблиця Дисперсионный анализ має таку структуру:

- df – кількість ступенів вільності (т; п-т-1; п-1);

- SS – дисперсія (факторна, залишкова, загальна);

- MS – дисперсія/кількість ступенів вільності;

- F – оцінка зв’язку між незалежними факторами залежною змінною;

- значимость F – рівень значущості, що відповідає визначеному F – чим він нижче, тим кращий зв’язок.

Таблиця Параметри модели має таку структуру:

- коэффициенты– значення параметрів моделі а₀ а_j

- стандартная ошибка – стандартна помилка параметрів рівняння;

- t-статистика – коефіцієнт/стандартна помилка;

- Р-значение – значущість для t-статистики;

- межі довірчих інтервалів для коефіцієнтів рівняння регресії при різних рівнях значущості.

Остання таблиця включає прогнозовані значення у ізалишки.

Одержане рівняння залежності можна використову­вати для прогнозних розрахунків. Підставивши у це рівняння нове значення х, можна одержати прогнозова­не значення у.

Для розширеного аналізу можна також розрахову­вати такий показник, як коефіцієнт еластичності:

, де a_j– коефіцієнт у рівнянні залежності для j-го фактора;

_j – серед­ньо­арифметичне значення j-го фактора;

– середньоарифметичне значення результативного показника.

Коефіцієнт еластичності показує, на скільки відсот­ків у середньому змі­ню­ється результативний показник із зміною аргументу х на 1 %.

При проведенні кореляційно-регресійного аналізу можна застосовувати також додаткові статистичні функ­ції для оцінювання параметрів моделі та залежності між факторами:

q НАКЛОН – визначає коефіцієнт a₁ у рівнянні у = a₀+ a₁ х;

q ОТРЕЗОК – визначає коефіцієнт a₀ у рівнянні у = a₀+ a₁ х;

q ЛИНЕЙН – вводяться масиви у та х (можна декіль­ка) – обчислюються коефіцієнти а₁ і a₀ або коефіцієнти у рівнянні з a_j. Вводити цю функцію у множинну регресію треба за правилами роботи з БД: виділити діапазон ре­зультатів (рядок із т + 1 клітинок); ввести функцію; вве­дення формули закінчити одночасним натисненням на клавіші Ctrl+Shift+Enter. Послідовність розміщення ре­зультатів відповідає параметрам моделі а _m. a_m-1,... а_1, a₀;

q ПИРСОН – визначає коефіцієнт кореляції R у ме­жах від -1 до +1;

q КВПІІРСОН – визначає коефіцієнт детермінації R²;

q СТОШУХ – визначає стандартну похибку прог­нозних значень у для кожного значення х регресії;

q КОВАР – визначає коефіцієнти коваріації, а та­кож середні попарні добутки відхилень.