Занятие 6
Иррациональные уравнения и неравенства
Общие сведения об уравнениях
О. 1.1. Областью допустимых значений уравнения (ОДЗ) называется множество тех значений неизвестной, при которых определены его правая и левая части.
Решить уравнение – это значит найти все его корни или доказать, что данное уравнение не имеет корней. Очевидно, что вне ОДЗ решений не существует, однако не все числа, входящие в ОДЗ, служат решениями уравнения. Уравнение можно решить и не находя ОДЗ. В некоторых случаях уравнение удобно решить путём подбора корней. При этом обязательно нужно доказать, что данное уравнение не имеет никаких других корней.
О. 1.2. Два уравнения называются равносильными, если множества их решений совпадают.
Если уравнение (1) равносильно уравнению (2), то записывают:
(1) 
(2).
О. 1.3. Если все корни уравнения (1) являются корнями уравнения (2), то говорят, что «уравнение (2) является следствием уравнения (1)». Записывают: (1) 
(2). При этом среди корней уравнения (2) могут быть посторонние корни (такие, которые не являются корнями уравнения (1)).
Способы решения иррациональных уравнений
О. 2.1. Иррациональным называется уравнение, в котором переменная или выражение, содержащее переменную, входит под знаком радикала.
Основная идея большинства способов решения иррациональных уравнений заключается, как правило, в сведении к рациональным алгебраическим уравнениям. Для решения иррациональных уравнений применяют следующие общие способы решения уравнений:
а) Путём равносильных преобразований. В этом случае нет необходимости делать проверку найденных корней.
б) Предварительное нахождение области определения уравнения (ОДЗ) и дальнейшее проведение преобразований уравнения, которые равносильны в пределах ОДЗ. В этом случае также нет необходимости делать проверку найденных корней, но необходимо выяснить, входят ли полученные корни в ОДЗ. Следует заметить, что нахождение ОДЗ может быть как чрезвычайно сложной с одной стороны, так и абсолютно необходимой, с другой стороны, задачей.
в) Способ возведения в степень, когда обе части иррационального уравнения последовательно возводят в одну и ту же степень. Преобразования такого уравнения, вообще говоря, не являются равносильными. При этом получается уравнение, являющееся следствием исходного уравнения. В результате таких преобразований могут быть получены «посторонние корни», которые должны быть устранены при помощи проверки. Отметим, что такой способ решения иррациональных уравнений зачастую позволяет без лишних усилий осуществить проверку корней.
Пример 1. Решить уравнение 
.
Δ Совершенно понятно, что поиск ОДЗ в данном примере сопряжён с определёнными трудностями. Однако попробуем решить это уравнение непосредственно. Поскольку мы будем лишь возводить в квадрат, то ОДЗ может лишь расшириться, то есть могут появиться посторонние корни. Однако эти корни мы можем отсеять проверкой.
Имеем:
, 
.
Проверка при помощи подстановки в первоначальное уравнение полученных значени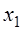й 
и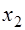 
показывает, что не является решением исходного уравнения, а 
является решением.
Ответ: 
.
Замечание. Способ решения иррационального уравнения, при котором обе его части последовательно возводят в степень с последующей проверкой корней, не удобен или вовсе не применим, когда проверка корней затруднительна. В таких случаях можно применить один из двух первых способов решения (а) или б)).
Таким образом, к понятию ОДЗ нужно относиться избирательно и искать его, только если в этом возникает существенная необходимость.
Пример 2. Решить уравнение 
.
Δ Найдём ОДЗ данного уравнения:
.
Возведём в квадрат обе части уравнения (они неотрицательны на ОДЗ). Получаем уравнение-следствие:
= 
.
ОДЗ, а значит, не может быть корнем исходного уравнения. Заметим также, что в процессе решения нам пришлось дважды возводить в квадрат, поэтому кроме условия 
, необходимо учитывать условие, 
откуда 
. Число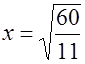 
удовлетворяет условиям: и . Следовательно 
- решение данного уравнения.
Ответ: 
