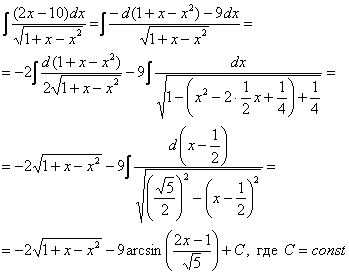Это заключительная часть урока, тем не менее, интегралы такого типа встречаются довольно часто! Если накопилась усталость, может, оно, лучше завтра почитать?;)
Интегралы, которые мы будем рассматривать, похожи на интегралы предыдущего параграфа, они имеют вид: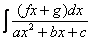 
или 
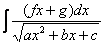(коэффициенты 
, 
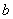и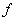 
не равны нулю).
То есть, в числителе у нас появилась линейная функция. Как решать такие интегралы?
Пример 14
Найти неопределенный интеграл:
Пожалуйста, будьте внимательны, сейчас мы рассмотрим типовой алгоритм.
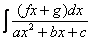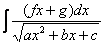1) Когда дан интеграл вида или (коэффициенты , 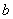и 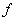не равны нулю), то первое, что мы делаем, это… берём черновик. Дело в том, что сейчас нам предстоит выполнить небольшой подбор.
2) Заключаем выражение, которое находится в знаменателе (неважно – под корнем или без корня) под знак дифференциала, в данном примере: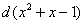 
3) Раскрываем дифференциал:
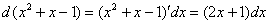
Смотрим на числитель нашего интеграла: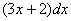 
Немного разные вещи получились…. А теперь нам нужно подобрать множитель для дифференциала 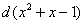, такой, чтобы при его раскрытии получилось, как минимум, 
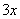. В данном случае подходящим множителем является: 
4) Для самоконтроля снова раскрываем наш дифференциал:
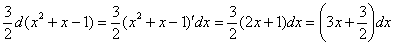
Снова смотрим на числитель нашего интеграла: .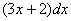
Уже ближе, но у нас не то слагаемое: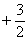 
5) К нашему дифференциалу :
– приписываем слагаемое, которое у нас изначально было в подынтегральной функции:
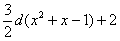
– Вычитаем (в данном случае – вычитаем, иногда нужно, наоборот, прибавлять) наше «не то» слагаемое: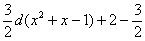 
– Обе константы берем в скобки и приписываем справа значок дифференциала:
– Вычитаем (в некоторых примерах нужно сложить) константы:
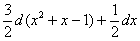
6) Выполняем проверку:
У нас получился в точности числитель подынтегральной функции, значит, подбор выполнен успешно.
Чистовое оформление решения выглядит примерно так:
(1) Выполняем на черновике подбор числителя согласно вышерассмотренному алгоритму. Обязательно выполняем проверку, правильно ли выполнен подбор. При определенном опыте решения интегралов подбор нетрудно выполнить и в уме.
(2) Почленно делим числитель на знаменатель. В практическом решении задач данный шаг можно опускать
(3) Используя свойство линейности, разделяем интегралы. Все константы целесообразно вынести за знаки интегралов.
(4) Первый интеграл фактически является табличным, используем формулу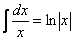 
(константу 
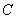припишем позже, когда возьмем второй интеграл). Во втором интеграле выделяем полный квадрат (такой тип интегралов мы рассмотрели в предыдущем параграфе).
Остальное дело техники.
И, на закуску, пара примеров для самостоятельного решения – один проще, другой сложнее.
Пример 15
Найти неопределенный интеграл:
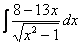
Пример 16
Найти неопределенный интеграл:
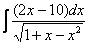
Для решения данных примеров будет полезен частный случай интегрирования степенной функции, которого нет в моей таблице: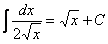 
Как видите, интегрирование дробей - дело кропотливое, часто приходится применять искусственные приемы и подборы. Но что делать…
Существуют и другие виды дробей, так называемые дробно-рациональные функции, они решаются методом неопределенных коэффициентов. Но это уже тема урока Интегрирование дробно рациональных функций.
Желаю успехов!
Решения и ответы:
Пример 2: Решение:
Пример 4: Решение:
Пример 7: Решение:
Пример 8: Решение:
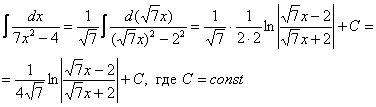
Пример 10: Решение:
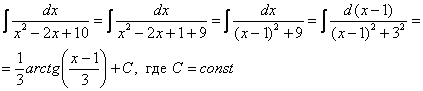
Пример 13: Решение:
Пример 15: Решение:
Пример 16: Решение:
