Часть 1
ЗАНЯТИЕ 1
ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ В РЕЗИСТИВНЫХ ЦЕПЯХ. СВЯЗЬ МЕЖДУ НАПРЯЖЕНИЯМИ И ТОКАМИ В ОСНОВНЫХ ЭЛЕМЕНТАХ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
Методические указания
Изучите теоретический материал по учебной литературе: [2, с.16–25].
Занятие проводится без выполнения подготовительного задания.
При решении задачи 1.1 учесть, что соединение сопротивлений называется последовательным, если ток в них один и тот же.
Эквивалентное сопротивление цепи, состоящей из последовательных сопротивлений, равно сумме этих сопротивлений.
Сопротивления параллельны, если они присоединены к одной и той же паре узлов.
При параллельном соединении складываются проводимости участков цепи. Эквивалентное сопротивление находят как величину, обратную эквивалентной проводимости цепи.
Смешанное соединение – это сочетание последовательного и параллельного соединений.
Для каждого варианта выполните задачи 1.1, 1.2. Номер варианта выбирается согласно указаниям преподавателя.
З а д а ч а 1.1
Определите входное сопротивление схемы относительно зажимов 1–1¢ (табл.1.1). Во всех схемах  10 Ом.
10 Ом.
Таблица 1.1
Исходные данные к задаче 1.1

Продолжение табл.1.1

Окончание табл.1.1

З а д а ч а 1.2
В соответствии с заданным вариантом (табл.1.2, рис.1.1) определите входное сопротивление схемы относительно зажимов а–в.
Таблица 1.2
Исходные данные к задаче 1.2
| Вариант | Схема рис.1.1 |  ,
Ом ,
Ом
|  ,
Ом ,
Ом
|  ,
Ом ,
Ом
|  ,
Ом ,
Ом
|  ,
Ом ,
Ом
| 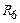 ,
Ом ,
Ом
| 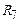 ,
Ом ,
Ом
|  ,
Ом ,
Ом
|
| а) | |||||||||
| б) | |||||||||
| в) | |||||||||
| г) | |||||||||
| д) | |||||||||
| а) |
Продолжение табл.1.2
| Вариант | Схема рис.1.1 |  ,
Ом ,
Ом
|  ,
Ом ,
Ом
|  ,
Ом ,
Ом
|  ,
Ом ,
Ом
|  ,
Ом ,
Ом
| 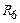 ,
Ом ,
Ом
| 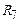 ,
Ом ,
Ом
|  ,
Ом ,
Ом
|
| б) | |||||||||
| в) | |||||||||
| г) | |||||||||
| д) | |||||||||
| а) | |||||||||
| б) | |||||||||
| в) | |||||||||
| г) | |||||||||
| д) | |||||||||
| а) | |||||||||
| б) | |||||||||
| в) | |||||||||
| г) | |||||||||
| д) | |||||||||
| а) | |||||||||
| б) | |||||||||
| в) | |||||||||
| г) | |||||||||
| д) | |||||||||
| а) | |||||||||
| б) | |||||||||
| в) | |||||||||
| г) | |||||||||
| д) |


Рис.1.1
З а д а ч а 1.3
Определите показание амперметра (рис.1.2), используя данные из табл.1.3.
Таблица 1.3
Исходные данные к задаче 1.3
| Вариант | Схема рис.1.2 | 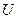 ,
В ,
В
|  ,
Ом ,
Ом
|  ,
Ом ,
Ом
|  ,
Ом ,
Ом
|  ,
Ом ,
Ом
|
| а) | ||||||
| б) | ||||||
| в) | ||||||
| г) | ||||||
| д) |
Продолжение табл.1.3
| Вариант | Схема рис.1.2 | 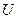 ,
В ,
В
|  ,
Ом ,
Ом
|  ,
Ом ,
Ом
|  ,
Ом ,
Ом
|  ,
Ом ,
Ом
|
| е) | ||||||
| б) | ||||||
| в) | ||||||
| г) | ||||||
| д) | ||||||
| е) | ||||||
| а) | ||||||
| б) | ||||||
| в) | ||||||
| г) | ||||||
| д) | ||||||
| е) | ||||||
| а) | ||||||
| б) | ||||||
| в) | ||||||
| г) | ||||||
| д) | ||||||
| е) | ||||||
| а) | ||||||
| б) | ||||||
| в) | ||||||
| г) | ||||||
| д) | ||||||
| е) |

Рис.1.2
З а д а ч а 1.4
Делитель напряжения, изображенный на рис.1.3, нагружен на бесконечно большое сопротивление. В соответствии с заданным вариантом определите величины, указанные в табл.1.4 знаком (?).

Рис.1.3
Таблица 1.4
Исходные данные к задаче 1.4
| Вариант |  ,
В ,
В
| 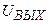 , В , В
|  ,
кОм ,
кОм
| 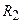 ,
кОм ,
кОм
|  ,
кОм ,
кОм
| Вариант |  ,В ,В
| 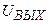 , В , В
|  ,
кОм ,
кОм
| 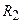 ,
кОм ,
кОм
|  ,
кОм ,
кОм
|
| ? | ? | ? | ? | ||||||||
| ? | ? | ? | ? | 0,5 | |||||||
| ? | ? | ? | |||||||||
| ? | ? | 0,5 | ? | 32,5 | 7,5 | ? | |||||
| ? | ? | ? | ? | ||||||||
| ? | ? | ? | |||||||||
| ? | ? | 7,5 | ? | ? | |||||||
| ? | ? | ? | ? | ||||||||
| ? | ? | ? | 9,5 | 0,5 | ? | ||||||
| ? | ? | ? | ? | 7,5 | |||||||
| ? | ? | ? | ? | ||||||||
| ? | ? | ? | ? | ||||||||
| ? | 52,5 | 7,5 | ? | ? | ? | ||||||
| ? | ? | ? | ? | ||||||||
| ? | ? | ? | 9,5 | 0,5 | ? |
З а д а ч а 1.5
Для схемы рис.1.4 определите значение сопротивления резистора R3 по данным табл.1.5.

Рис.1.4
Таблица 1.5
Исходные данные к задаче 1.5
| Вариант |  , В , В
| R11, Ом | R12, Ом | R21, Ом | R22, Ом | Заданная величина |
| I1= 2 A | ||||||
| I2= 1 A | ||||||
| U11= 4 B | ||||||
| U12= 20 B | ||||||
| U21= 10 B | ||||||
| U22= 9 B | ||||||
| I1= 4 A | ||||||
| I2= 2,5 A | ||||||
| U11= 90 B | ||||||
| U12= 16 B | ||||||
| U21= 100 B | ||||||
| U22= 15 B | ||||||
| I1= 6 A | ||||||
| I2= 3,5 A | ||||||
| I3= 4 A | ||||||
| U11= 900 B | ||||||
| U12= 250 B | ||||||
| U21= 110 B | ||||||
| U22= 180 B | ||||||
| U11= 1040 B | ||||||
| U12= 140 B | ||||||
| U21= 375 B | ||||||
| U22= 240 B | ||||||
| U11= 238 B | ||||||
| U12= 90 B | ||||||
| U21= 950 B | ||||||
| U22= 50 B | ||||||
| U11= 1365 B | ||||||
| U12= 220 B | ||||||
| I2= 11,5 A |
ЗАНЯТИЕ 2
РАСЧЕТ СИНУСОИДАЛЬНЫХ ТОКОВ И НАПРЯЖЕНИЙ В ПРОСТЫХ ЛИНЕЙНЫХ ЦЕПЯХ С РЕЗИСТИВНЫМИ, ИНДУКТИВНЫМИ И ЕМКОСТНЫМИ ЭЛЕМЕНТАМИ
Методические указания
Изучите теоретический материал по учебной литературе: [1, с.171–179; 191–201]; [2, с.72–105; 108–115; 119–124]; [3, с.63–86; 92–94] и ответьте на следующие вопросы:
1. Объясните смысл выражений «двухполюсник», «линейный пассивный двухполюсник».
2. Дайте определение резистивного элемента R и приведите выражения для вычисления напряжения на резисторе через ток в нем и обратно: выражение для вычисления тока в резисторе через напряжение на нем. Когда резистор считается линейным?
3. То же – в отношении индуктивного элемента L.
4. То же – в отношении индуктивного элемента С.
5. При каких условиях электрическая цепь считается линейной?
6. Как выглядят выражения мгновенных значений синусоидальных токов и напряжений как функций времени?
7. Как сформировать амплитудный комплекс (символическое изображение) синусоидального тока в показательной форме?
8. То же – синусоидального напряжения?
9. Пусть известны символические изображения (например, – амплитудные комплексы) синусоидального тока  и напряжения
и напряжения  .
.
Как получить изображения производной и интеграла от этих синусоидальных функций времени?
10.Пусть в каждом из трех элементов: резисторе R, индуктивности L, емкости С – ток синусоидальный  . Его символическое изображение (амплитудный комплекс)
. Его символическое изображение (амплитудный комплекс)  . Синусоидальные напряжения в каждом из трех элементов соответственно равны:
. Синусоидальные напряжения в каждом из трех элементов соответственно равны:
 ,
,
 ,
,
 .
.
Выразите символические изображения напряжений  ,
,  ,
, 
через  .
.
11.Сформулируйте закон Ома для пассивного линейного двухполюсника в символической форме.
12. Синусоидальные напряжения и ток на входе линейного пассивного двухполюсника заданы своими действующими комплексами: 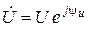 ,
,  . Покажите, как в этом случае для данного двухполюсника вычислить эквивалентные (входные) комплексное сопротивление
. Покажите, как в этом случае для данного двухполюсника вычислить эквивалентные (входные) комплексное сопротивление  R+jX, комплексную проводимость
R+jX, комплексную проводимость  G –jB.
G –jB.
Приведите формулы, позволяющие вычислить активную G и реактивную В проводимости через активное R и реактивное X сопротивления, и обратно: R, X – через G, B.
При выполнении задачи 2.1. рекомендуется воспользоваться соотношениями, которые устанавливают связь между напряжениями и токами в отдельных элементах цепи.
При выполнении задач 2.3 – 2.5 воспользуйтесь комплексным методом. Заданную функцию и сопротивления цепи записывайте в комплексной форме. Задачи решайте с использованием законов Ома и Кирхгофа в комплексной форме. Искомую функцию найдите как комплексную величину, затем перейдите от комплексной амплитуды к мгновенному значению.
З а д а ч а 2.1
По номеру варианта выберите схему (рис.2.1) и заданные величины из табл.2.1, выполните задания, указанные в таблице.

Рис.2.1
Таблица 2.1
Исходные данные к задаче 2.1
| Вариант | Схема рис.2.1 | Параметры цепи | Заданная функция | Получить выражение | Построить кривые (качественно) | |||
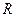
| 
| 
| 
| |||||
| Ом | мГн | мкФ | 1/сек | |||||
| в) | – | – | 
| 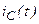
|  , , 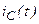
| |||
| б) | – | – | 
| 
|  , , 
| |||
| в) | – | – | 
| 
| 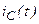 , , 
| |||
| б) | – | – | 
| 
|  , , 
| |||
| а) | – | – | 
| 
|  , , 
| |||
| в) | – | – | 
| 
| 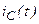 , , 
| |||
| в) | – | – | 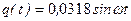
| 
| 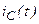 , , 
| |||
| а) | – | – | 
| 
|  , , 
| |||
| в) | – | – | 
| 
| 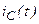 , , 
|






