Анализ распределения крутящих моментов MK рассмотрим на примере бруса, изображенного на рис.1.5,а.
I. Составляем уравнение равновесия бруса (рис. 1.5,б)
∑ MZ = 0; 
и находим реактивный момент МС в заделке С
MC = 3m.
2. Выделяем участки бруса: 1 участок – AB, 0 
, 2 участок – BC, 
3. Применяя метод сечений к каждому участку (рис. 1.5, в, г), находим внутренние крутящие моменты для 1 и 2 участков:
4. По полученным значениям внутренних моментов строим эпюру с учетом правила знаков для внутренних моментов (рис. 1.5, д).
Анализ внутренних силовых факторов при изгибе
При изгибе бруса (балки) в поперечных сечениях могут возникать два силовых фактора – поперечная сила Q и изгибающий момент M. Для их определения применяем метод сечений. Мысленно рассекая балку поперечной плоскостью, прикладываем в сечении поперечную силу 
и изгибающий момент 
, имеющие положительные направления в соответствии с принятым правилом знаков. Эти силовые факторы определим из уравнений равновесия частей балки.
Рассмотрим двухопорную балку (рис. 1.6, а), нагруженную сосредоточенной силой P.
Из уравнений равновесия балки определяем силы реакций в опорах 
и 
(рис. 1.6, б):
, 
; 
, 
.
Балка имеет два участка: 0 
и 
.
Применяя метод сечений, получаем:
на 1 участке
, 
;
на 2 участке
, 
.
Эпюры и 
показаны на рис. 1.6, в. Поперечная сила в пределах каждого участка постоянна, а изгибающий момент изменяется по линейному закону.
Рассмотрим двухопорную балку, нагруженную сосредоточенным моментом m (рис. 1.7, а) (круговая стрелка на рис. 1.7 указывает направление вращения).
Составив уравнения равновесия балки, определяем силы реакций в опорах и (рис. 1.7, б):
, 
; , 
.
Рис. 1.6.
Рис. 1.7.
Рис 1.8.
Балка имеет два участка: 0 и .
Применяя метод сечений на первом участке, получаем:
, 
;
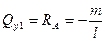на 2 участке
, 
.
Эпюры и показаны на рис. 1.7, в. Поперечная сила постоянна по всей длине балки, а изгибающий момент изменяется по линейному закону в пределах каждого участка.
Рассмотрим двухопорную балку, нагруженную распределенной нагрузкой постоянной интенсивности q (рис. 1.8, а).
Используя уравнение равновесия балки, определяем силы реакций в опорах 
и (1.8, б):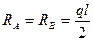 
.
Балка имеет один участок.
Применяя метод сечений, получаем:
, 
.
Эпюры и показаны на рис. 1.8, в. Поперечная сила изменяется по линейному закону, а изгибающий момент – по закону квадратной параболы. В сечении 
, а изгибающий момент имеет максимальное значение 
.
Дифференциальные зависимости между
Изгибающим моментом, поперечной силой и
