Построим эффективный алгоритм вычисления корней уравнения. Пусть задано начальное приближение 
. Вычислим в этой точке значение функции 
и её производной 
. Рассмотрим графическую иллюстрацию метода:
.
Далее получим следующее приближение в точке 
, проводя касательную из точки (
) до пересечения с осью абсцисс:
Продолжая этот процесс, получим известную формулу Ньютона:
(3.10)
 |
x
Рис. 3.3. Графическая иллюстрация метода Ньютона
Рассмотрим решение нелинейного уравнения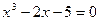 
методом Ньютона в пакете Excel. В качестве начального значения взято =3, которое удовлетворяет условию 
>0. Заданная точность 
. Дальнейшие вычисления приведем в виде таблицы (таб.3.2.).
Таблица 3.2. Вспомогательная таблица для вычисления корней нелинейного уравнения 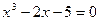методом Ньютона
| k | xk | f(xk) | f|(xk) | (xk+1 - xk)<eps |
| 16,0000000 | - | |||
| 2,36 | 3,4242560 | 14,7088 | нет | |
| 2,127197 | 0,3710998 | 11,5749 | нет | |
| 2,095136 | 0,0065266 | 11,16879 | нет | |
| 2,094552 | 0,0000021 | 11,16144 | нет | |
| 2,094551 | 0,0000000 | 11,16144 | да |
В пакете Mathcad для решения уравнения 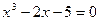методом Ньютона используется ряд формул:
Корень уравнения равен 2,094551 и достигнут за 17 шагов.
Метод Ньютона (касательных) характеризуется квадратичной скоростью сходимости, т.е. на каждой итерации удваивается число верных знаков. Однако этот метод не всегда приводит к нужному результату. Рассмотрим этот вопрос подробнее.
Преобразуем уравнение (3.1) к эквивалентному уравнению вида:
x=g(x) (3.11)
В случае метода касательных 
. Если известно начальное приближение к корню x=x0, то следующее приближение найдем из уравнения x1=g(x0), далее x2=g(x1),... Продолжая этот процесс, получим рекуррентную формулу метода простой итерации
xk+1=g(xk) (3.12)
Итерационный процесс продолжается до тех пор, пока не будут выполнены условия (3.5-3.7).
Всегда ли описанный вычислительный процесс приводит к искомому решению? При каких условиях он будет сходящимся? Для ответа на эти вопросы опять обратимся к геометрической иллюстрации метода.
Корень уравнения представляется точкой пересечения функций y=x и y=g(x). Как видно из рис. 3а, если выполняется условие 
, то процесс сходится, иначе – расходится (рис3.4б).
(a) (б)
Рис. 3.4. Сходимость итерационных методов: а) процесс сходится;
б) процесс расходится.
Изучая самостоятельно условия сходимости, убедитесь, что интервал 
более предпочтителен, чем 
, поскольку на нем наблюдается двухсторонняя сходимость к корню.
Итак, для того чтобы итерационный процесс был сходящимся и приводил к искомому результату, требуется выполнение условия:
(3.13)
Переход от уравнения f(x)=0 к уравнению х=g(x) можно осуществлять различными способами. При этом важно, чтобы выбранная функция g(x) удовлетворяла условию (3.13). К примеру, если функцию f(x) умножить на произвольную константу q и добавим к обеим частям уравнения (3.1) переменную х, то g(x)=q*f(x)+x. Выберем константу q такой, чтобы скорость сходимости алгоритма была самой высокой. Если 1<g’(x)<0, то сходимость итерационного процесса будет двусторонней. Производная по х от этой функции: 
. Наибольшую сходимость получим при g’(x)=0, тогда 
и формула (3.12) переходит в формулу Ньютона (3.10).
Метод Ньютона обладает высокой скоростью сходимости, однако он не всегда сходится. Условие сходимости , где g(x) = x – f(x)/ f’(x), сводится к требованию 
.
В практических расчетах важно выбирать начальное значение как можно ближе к искомому значению, а в программе устанавливать «предохранитель от зацикливания».
Недостатком метода является и то, что на каждом шаге необходимо вычислять не только функцию, но и ее производную. Это не всегда удобно. Одна из модификаций метода Ньютона - вычисление производной только на первой итерации:
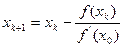(3.14)
Другой метод модификации – замена производной конечной разностью
(3.15)
тогда
(3.16)
Геометрический смысл такого изменения алгоритма Ньютона состоит в том, что от касательной мы приходим к секущей. Метод секущих уступает методу Ньютона в скорости сходимости, но не требует вычисления производной. Заметим, что этот метод близок к методу хорд (3.9), однако, в отличие от него, начальные приближения в методе секущих могут располагаться как с разных сторон от корня, так и с одной стороны.
Дополнительное задание: основываясь на алгоритме Горнера, составьте программу табуляции и решения алгебраических уравнений.
