Лабораторная работа №3.
Численные методы решения нелинейных уравнений
Введение
Рассмотрим задачу нахождения корней нелинейного уравнения
f(x)=0 (3.1)
Корнями уравнения (3.1) называются такие значения х, которые при подстановке обращают его в тождество. Только для простейших уравнений удается найти решение в виде формул, т.е. аналитическом виде. Некоторые из таких уравнений подробно изучались в школьном курсе математики. Чаще приходится решать уравнения приближенными методами, наибольшее распространение среди которых, в связи с появлением компьютеров, получили численные методы. В этой работе познакомимся с некоторыми из них.
Алгоритм нахождения корней приближенными методами можно разбить на два этапа. На первом изучается расположение корней и проводится их разделение. Находится область [a,b], в которой существует корень уравнения или начальное приближение к корню x0. Простейший способ решения этой задачи является исследование графика функции f(x). В общем же случае для её решения необходимо привлекать все средства математического анализа.
Существование на найденном отрезке [a,b], по крайней мере, одного корня уравнения (3.1) следует из условия Больцано:
f(a) * f(b) < 0 (3.2)
При этом подразумевается, что функция f(x) непрерывна на данном отрезке. Однако данное условие не отвечает на вопрос о количестве корней уравнения на заданном отрезке [a,b]. Если же требование непрерывности функции дополнить ещё требованием её монотонности, а это следует из знакопостоянства первой производной 
, то можно утверждать о существовании единственного корня на заданном отрезке.
При локализации корней важно так же знание основных свойств данного типа уравнения. К примеру, напомним, некоторые свойства алгебраических уравнений:
, (3.3)
где 
вещественные коэффициенты.
а) Уравнение степени n имеет n корней, среди которых могут быть как вещественные, так и комплексные. Комплексные корни образуют комплексно-сопряженные пары и, следовательно, уравнение имеет четное число таких корней. При нечетном значении n имеется, по меньшей мере, один вещественный корень.
б) Число положительных вещественных корней меньше или равно числа перемен знаков в последовательности коэффициентов 
. Замена х на –х в уравнении (3.3) позволяет таким же способом оценить число отрицательных корней.
На втором этапе решения уравнения (3.1), используя полученное начальное приближение, строится итерационный процесс, позволяющий уточнять значение корня с некоторой, наперед заданной точностью 
. Итерационный процесс состоит в последовательном уточнении начального приближения. Каждый такой шаг называется итерацией. В результате процесса итерации находится последовательность приближенных значений корней уравнения 
. Если эта последовательность с ростом n приближается к истинному значению корня x, то итерационный процесс сходится. Говорят, что итерационный процесс сходится, по меньшей мере, с порядком m, если выполнено условие:
, (3.4)
где С>0 некоторая константа. Если m=1, то говорят о сходимости первого порядка; m=2 - о квадратичной, m=3 - о кубической сходимостях.
Итерационные циклы заканчиваются, если при заданной допустимой погрешности выполняются критерии по абсолютным или относительным отклонениям:
; 
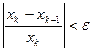(3.5,3.6)
или малости невязки:
(3.7)
Эта работа посвящена изучению некоторых класических алгоритмом решения нелинейных уравнений, их скоростей сходимости, влиянию на сходимость выбора начального приближения и другим вопросам.
Отделение корней уравнения
Для отделения действительных корней полезно заранее определить верхние и нижние границы их расположения. Для этого используем следующую методику вычислений.
Кольцо, в котором расположены корни уравнения, вычисляют по следующей формуле:
r ≤ | x*i| ≤ R, (3.8)
где x*i - точные корни уравнения,
, 
,
А = max 
, B = max 
.
Соответственно положительные корни будут находиться на интервале:
r < x*i+ < R,
а отрицательные:
- R < x*i ¯ < - r.
Также интервал расположения корней можно определить графически. Приведем пример отделения корней для уравнения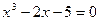 
.
По формуле (3.8) кольцо, в котором расположены корни, будет [0.714, 6]. Отсюда, положительные корни находятся на отрезке [0.714, 6], а отрицательные – [-6, -0,714]. Для уточнения границ отрезков можно построить график (рис.3.1.)
Рис. 3.1. График функции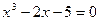
Из рис.3.1. видно, что интервал для положительного корня можно сузить до отрезка [1, 3]. Для дальнейшего вычисления положительного корня уравнения будем использовать полученный отрезок.
