КОНТРОЛЬНАЯ РАБОТА
По дисциплине
«ОСНОВЫ ФИНАНСОВЫХ ВЫЧИСЛЕНИЙ»
| СТУДЕНТ: | Петрухина Т.К. |
| КУРС: | 3 |
| НАПРАВЛЕНИЕ: | Экономика |
| ПРОФИЛЬ: | Финансы и кредит |
| № ЗАЧ. КНИЖКИ: | 12ФЛД11234 |
| ПРЕПОДАВАТЕЛЬ: | Малашенко В.М. |
Брянск 2014
ЗАДАНИЕ
Выполнить различные финансовые расчеты, используя следующие исходные данные:
| Вариант | Сумма P, S или R | Дата начальная T н | Дата конечная T к | Время в днях Т дн | Время в годах Т лет | Ставка i, j или i э | Число начислений процентов m или платежей в году p |
| 20.01.2014 | 17.03.2014 |
Расчеты выполнить вручную и с использованием табличного процессора Microsoft Excel.
Задача 1. Банк выдал ссуду размером P =1 000 000 руб. Дата выдачи ссуды — 20.01.2014 г., возврата — 17.03.2014 г. День выдачи и день возврата считать за один день. Простые проценты рассчитываются по ставке i =12% годовых. Найти проценты I:
1) точные с точным числом дней ссуды;
2) обыкновенные с точным числом дней ссуды;
3) обыкновенные с приближенным числом дней ссуды.
Решение. Определим число дней ссуды:
· точное —
;
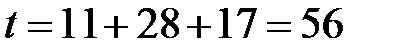· приближенное —
.
Действительное число дней в 2014 году — 365 (год невисокосный).
1. Точные проценты с точным числом дней ссуды («365/365»):
руб.
2. Обыкновенные проценты с точным числом дней ссуды («365/360»):
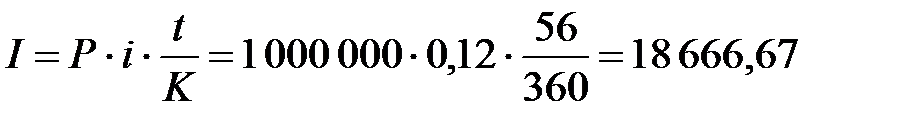руб.
3. Обыкновенные проценты с приближенным числом дней ссуды («360/360»):
руб.
Задача 2. Через t =90 дней после подписания договора должник уплатит S =1 000 000 руб. Кредит выдан под i =12% годовых (проценты простые, обыкновенные). Какова первоначальная сумма ссуды Р?
Решение. Так как проценты обыкновенные, временная база составляет K =360 дней. Первоначальная сумма ссуды Р или, что одно и тоже, современная стоимость выплачиваемой в будущем суммы S, определяется ее математическим дисконтированием по ставке простых процентов:
руб.
Задача 3. Через t =90 дней предприятие должно получить по векселю S =1 000 000 руб. Банк приобрел этот вексель с дисконтом и учел его по простой учетной ставке d =12% годовых (временная база равна 360 дням). Определить полученную предприятием сумму P и дисконт D.
Решение. За вексель предприятие получило в банке
руб.
Доход банка в виде дисконта составил
руб.
Задача 4. В кредитном договоре на сумму P =1 000 000 руб. и сроком на n =3 года зафиксирована ставка сложных процентов i =12% годовых. Определить наращенную сумму S к концу срока ссуды.
Решение. Наращенная сумма к концу срока ссуды составит
руб.
Задача 5. Ссуда размером P =1 000 000 руб. предоставлена на n =3 года. Сложные проценты начисляются и капитализируются m =2 раза в году, исходя из номинальной ставки j =12% годовых. Вычислить наращенную сумму S к концу срока ссуды.
Решение. Наращенная сумма к концу срока ссуды составит
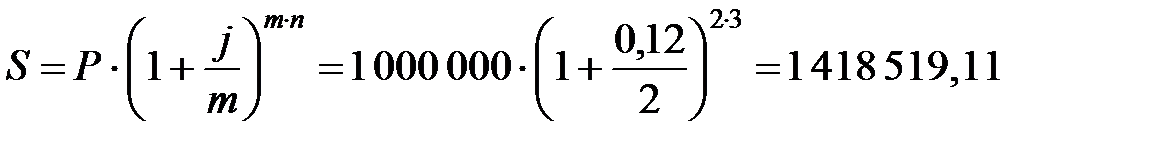руб.
Задача 6. Вычислить эффективную годовую процентную ставку i э, если банк начисляет и капитализирует проценты m =2 раза в году, исходя из номинальной ставки j =12% годовых.
Решение. Эффективная процентная ставка составляет
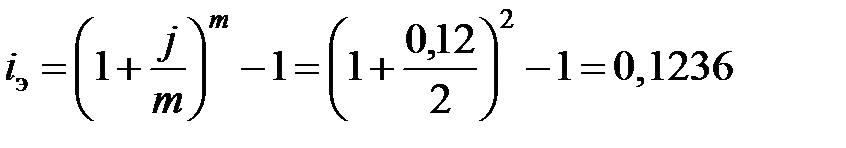или 12,36% годовых.
Задача 7. Определить, какой должна быть номинальная годовая процентная ставка j при начислении и капитализации процентов m =2 раза в году, чтобы обеспечить эффективную процентную ставку i э=12% годовых.
Решение. Номинальная процентная ставка должна быть равной
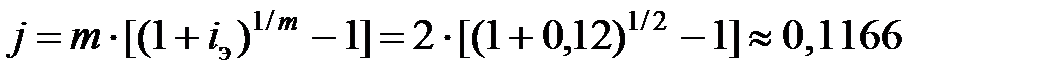или 11,66% годовых.
Задача 8. Через n =3 года предприятию будет выплачена сумма S =1 000 000 руб. Определить ее современную стоимость P при условии, что применяется ставка сложных процентов i =12% годовых.
Решение. Современная стоимость P будущей суммы S =1 000 000 руб. определяется математическим дисконтированием по ставке сложных процентов:
руб.
Задача 9. Через n =3 года по векселю должна быть выплачена сумма S =1 000 000 руб. Банк учел вексель по сложной учетной ставке d =12% годовых. Определить полученную векселедержателем сумму P и дисконт D.
Решение. При учете векселя векселедержатель получит
руб.
Размер дисконта равен
руб.
Задача 10. В течение n =3 лет на депозитный счет в банке в конце каждого года поступает по R =1 000 000 руб., на которые один раз в год начисляются сложные проценты по ставке i =12% годовых. Определить наращенную сумму S на счете к концу указанного срока и ее современную стоимость А.
Решение. Данный поток платежей является обычной годовой рентой с параметрами:
· платеж по ренте R =1 000 000 руб.;
· процентная ставка i =12% годовых;
· срок ренты n =3 года.
Наращенная сумма ренты к концу ее срока составит
руб.
Современная стоимость ренты равна
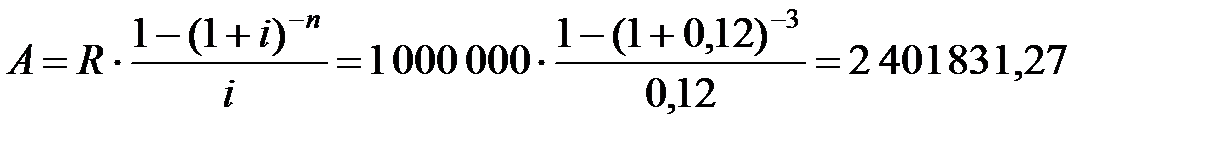руб.
Задача 11. В течение n =3 лет на депозитный счет в банке через равные интервалы времени p =2 раза в году в конце каждого периода поступает по R =1 000 000 руб., на которые m =2 раза в году (m = p) начисляются сложные проценты по номинальной ставке j =12% годовых. Определить наращенную сумму S на счете к концу указанного срока и ее современную стоимость А.
Решение. Данный поток платежей является р -срочной рентой постнумерадо с начислением и капитализацией процентов m раз в году (p = m). Рента имеет следующие параметры:
· платеж по ренте R =1 000 000 руб.;
· число платежей в году р =2;
· номинальная ставка j =12% годовых;
· число периодов начисления процентов в году m =2;
· срок ренты n =3 года.
Наращенная сумма ренты к концу ее срока составит
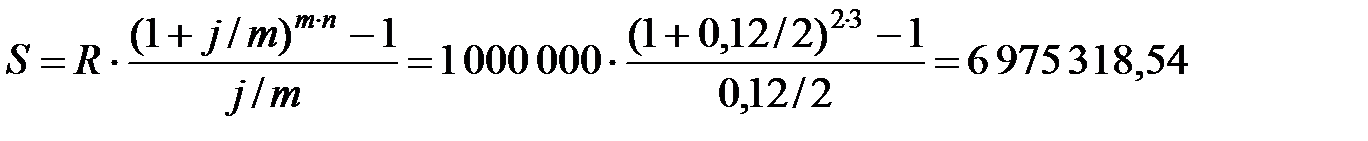руб.
Современная стоимость ренты равна
руб.
ПРИЛОЖЕНИЕ: компьютерные распечатки.
ЛИТЕРАТУРА
1. Брусов П. Н., Брусов П.П., Орехова Н.П., Скородулина С.В., Финансовая математика, Учебное пособие для бакалавров, Кнорус, 2014. — 253 с.
2. Брусов П. Н., Брусов П.П., Орехова Н.П., Скородулина С.В., Задачи по финансовой математике, Учебное пособие для бакалавров, Кнорус, 2014.
3. Брусов П. Н., Филатова Т. В., Финансовая математика, Учебное пособие для магистров: Инфра–М, 2014.
4. Четыркин Е. М. Финансовая математика. М.; Дело, 2001.
5. Малыхин В. И. Финансовая математика. М.; ЮНИТИ–ДАНА, 2000.
6. Брусов П. Н., Филатова Т. В. Применение математических методов в финансовом менеджменте: Учебное пособие, части 1,2. М.: Финансовая академия при Правительстве РФ, 2007.
7. Брусов П. Н., Филатова Т. В. Применение математических методов в финансовом менеджменте: Учебное пособие, части 3,4. М.: Финансовая академия при Правительстве РФ, 2010.
8. Брусов П. Н., Филатова Т. В. Финансовый менеджмент. Учебное пособие, том.I–III. М.: Кнорус, 2011.
9. Филатова Т. В. Финансовый менеджмент. Учебное пособие, М.: Инфра–М, 2010.
10. Брусов П. Н., Филатова Т. В., Лахметкина Н.И. Инвестиционный менеджмент. Учебное пособие: Инфра–М, 2014.
11. Брусов П. Н., Филатова Т. В., Орехова Н.П. Современные корпоративные финансы и инвестиции. Монография: Кнорус, 2014.
12. Попов В.Ю., Шаповал А.Б. Инвестиции. Математические методы. М.:Форум, 2008.
