В компьютерной технике очень часто используется двоичная система счисления. Двоичная система счисления является позиционной системой. В ней используется две цифры: 0 и 1. В двоичной системе счисления всего две цифры, называемые двоичными (binary digits). Сокращение этого наименования привело к появлению термина бит, ставшего названием разряда двоичного числа. Веса разрядов в двоичной системе изменяются по степеням двойки. Поскольку вес каждого разряда умножается либо на 0, либо на 1, то в результате значение числа определяется как сумма соответствующих значений степеней двойки. Если какой–либо разряд двоичного числа равен 1, то он называется значащим разрядом. Запись числа в двоичном виде намного длиннее записи в десятичной системе счисления. При выполнении различных операций в современных цифровых системах числа обычно представляются в двоичной системе счисления, основанием которой является число 2. Перевод десятичного числа в двоичный код можно осуществлять путем последовательного деления числа на 2. Остатки (0 или 1), получающиеся на каждом шаге деления, формируют двоичный код преобразуемого числа, начиная с его младшего разряда. В качестве старшего разряда двоичного кода записывается 1, полученная в результате последнего шага деления. Например, преобразование числа 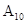 =109 в двоичный код выполняется следующим образом:
=109 в двоичный код выполняется следующим образом:

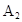 : остатки 109 2
: остатки 109 2




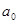 =1 54 2
=1 54 2


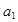 =0 27 2
=0 27 2


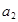 =1 13 2
=1 13 2


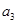 =1 6 2
=1 6 2

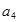 =0 3 2
=0 3 2



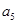 =1 1
=1 1

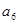 =
=
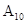 =109=
=109= 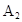 =
= 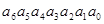 =1101101
=1101101
Обратное преобразование выполняется следующим образом:
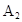 =
= 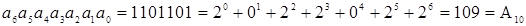
1 0 1 1 0 1 1
Перевод чисел из двоичной системы счисления в восьмеричную. Для записи двоичных чисел используются две цифры, то есть в каждом разряде числа возможны 2 варианта записи. Решаем показательное уравнение: 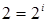 . Так как
. Так как 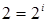 , то
, то 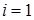 бит. Каждый разряд двоичного числа содержит 1 бит информации. Для записи восьмеричных чисел используются восемь цифр, то есть в каждом разряде числа возможны 8 вариантов записи. Решаем показательное уравнение:
бит. Каждый разряд двоичного числа содержит 1 бит информации. Для записи восьмеричных чисел используются восемь цифр, то есть в каждом разряде числа возможны 8 вариантов записи. Решаем показательное уравнение: 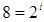 . Так как
. Так как 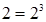 , то
, то 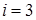 бита. Каждый разряд восьмеричного числа содержит 3 бита информации. Таким образом, для перевода целого двоичного числа в восьмеричное его нужно разбить на группы по три цифры, справа налево, а затем преобразовать каждую группу в восьмеричную цифру. Если в последней, левой, группе окажется меньше трех цифр, то необходимо ее дополнить слева нулями. Переведем таким способом двоичное число
бита. Каждый разряд восьмеричного числа содержит 3 бита информации. Таким образом, для перевода целого двоичного числа в восьмеричное его нужно разбить на группы по три цифры, справа налево, а затем преобразовать каждую группу в восьмеричную цифру. Если в последней, левой, группе окажется меньше трех цифр, то необходимо ее дополнить слева нулями. Переведем таким способом двоичное число 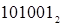 в восьмеричное:
в восьмеричное: 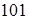
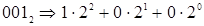
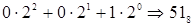 . Для упрощения перевода можно заранее подготовить таблицу преобразования двоичных триад (групп по 3 цифры) в восьмеричные цифры (табл. 1.3):
. Для упрощения перевода можно заранее подготовить таблицу преобразования двоичных триад (групп по 3 цифры) в восьмеричные цифры (табл. 1.3):
Таблица 1.3






