Внутренние силовые факторы представляют собой статические эквиваленты внутренних сил в виде сосредоточенных сил или моментов, возникающих в сечении стержня. Оценка прочности элемента конструкции или его материала по внутренним силовым факторам не может быть достаточной, так как при их определении не учитываются размеры сечений и характер распределения по ним внутренних сил. Поэтому пользуются характеристикой внутренних сил, называемой напряжением, которая позволяет учитывать размеры сечения и распределение внутренних сил.
Напряжение – это мера интенсивности внутренних сил в точке.
Рассмотрим произвольное сечение стержня, нагруженного силами Р 1, Р 2, Р 3 … Pi (рисунок 1.2). В этом сечении возникают внутренние силы, каким-либо образом распределенные по площади сечения.

Рисунок 1.2
В окрестностях некоторой точки К выделим элементарную площадку DS. Пусть DR – равнодействующая всех внутренних сил, действующих на DS. Уменьшаем DS до нуля, стягивая площадку до точки К, в пределе получим:
 ,
,
где р – полное напряжение в точке К.
Таким образом, получим:
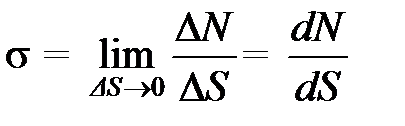 ,
,
где s – нормальное напряжение; D N – нормальная составляющая D R (см. рисунок 1.2,а);
 ,
,
где t – касательное напряжение; DТ – касательная составляющая DR (см. рисунок 1.2, а).
Полное напряжение р в точке К, как векторная величина, может быть представлено в виде составляющих: нормального напряжения s и касательного напряжения t, которое, в свою очередь, может быть представлено в виде t ху и t xz (рисунок 1.2, б).
Скалярная величина полного напряжения
 .
.
Разложение полного напряжения р на нормальное s и касательное t имеет особый смысл при расчетах на прочность. Нормальные напряжения возникают, когда внутренние силы стремятся сблизить или удалить отдельные частицы тела по направлению нормали к плоскости сечения, а касательные – когда внутренние силы стремятся сдвинуть одни частицы тела относительно других параллельно плоскости сечения. Практика показывает, что материалы сопротивляются нормальным и касательным напряжениям различным образом.
Если через точку К (рисунок 1.2) провести какое-либо другое сечение (и выделить новые площадки), то в этой точке будет другое полное напряжение р и другие соответствующие ему s и t.
Вырезав вокруг какой-нибудь точки тела элемент в виде бесконечно малого кубика, по его граням, в общем случае, можно показать действующее напряжение на трех взаимно перпендикулярных площадках, проходящих через эту точку (рисунок 1.3).

Рисунок 1.3
Совокупность напряжений на всех площадках, которые можно провести через любую точку нагруженного тела, называется напряженным состоянием в данной точке.
Если по граням кубика действуют только нормальные напряжения (касательные равны нулю), то такие напряжения называются главными, а площадки, на которых они действуют, называются главными площадками. В теории сопротивления материалов доказывается, что в каждой точке нагруженного тела существуют три главные взаимно перпендикулярные площадки. Главные напряжения на них обозначают s1, s2 и s3 (см. рисунок 1.4), при этом соотношение их по алгебраической величине, соответственно: s1 > s2 > s3.

Рисунок 1.4
Различные виды напряженного состояния характеризуются числом возникающих главных напряжений в точке тела. Если все три главных напряжения не равны нулю, то напряженное состояние называется объемным или трехосным (рисунок 1.4). Если равно нулю одно из главных напряжений, то напряженное состояние называется плоским или двухосным. Если равны нулю два главных напряжения, то напряженное состояние называется линейным или одноосным.
Любопытно, что, зная все напряжения на каких-либо трех взаимно перпендикулярных площадках (рисунок 1.3), можно с помощью несложных аналитических зависимостей определить такие же напряжения на любых других трех взаимно перпендикулярных площадках, в том числе и на главных площадках, проходящих через одну и ту же точку. Доказывается, что наибольшее и наименьшее по абсолютной величине нормальные напряжения smax и smin в точке развиваются на главных площадках. Т.е. для случая объемного напряженного состояния, изображенного на рисунке 1.4, smax = s1, smin= s3, а наибольшее касательное напряжение tmax развивается на площадках, находящихся под углом 45° к главным.
Зная напряженное состояние в любой точке элемента конструкции, можно оценить его прочность. В случае линейного и, в некоторых случаях, плоского напряженного состояния условие прочности можно записать в виде:
smax £ [s] или
t max £ [t],
где smax и t max – максимальные нормальное и касательное напряжения, которые рассчитываются по действующим силовым факторами и геометрическим характеристикам сечения стержня, испытывающего тот или иной вид деформации (как это делается – будет рассмотрено далее); [s] и [t] (s аdm и t аdm – международное обозначение) – допускаемые значения нормального и касательного напряжений, которые обычно определяются следующим образом:
[s] = sпр / [ n ] и [t] = tпр / [ n ],
где sпр и tпр – предельные напряжения, при достижении которых происходит разрушение материала элемента конструкции или утрата его работоспособности;
[ n ] (nadm) – нормируемый коэффициент запаса прочности.
Предельные напряжения определяются экспериментально, например, при испытании образцов на разрыв или сжатие, срез и т.д. При статическом нагружении элементов конструкции из пластических материалов обычно принимают:
sпр = sТ,
где sТ (s е) – предел текучести; а для хрупких материалов:
sпр = sв,
где sв (s u) – предел прочности.
Нормируемый коэффициент запаса прочности [ n ] вводится для учета возможных неблагоприятных отклонений свойств материала, условий работы конструкции, его величина назначается с учетом опыта эксплуатации сооружений и машин.
В более сложных случаях плоского напряженного состояния или при объемном нагружении оценка прочности производится по эквивалентному напряжению sэкв (s red) в соответствии с той или иной теорией прочности.
2. ЗАДАЧА № 1. «Расчёт стержня при центральном растяжении или сжатии»
Центральным растяжением или сжатием называют такой вид деформации, при котором в поперечных сечениях стержня возникает только один силовой фактор – продольная сила Nх, линия действия которой совпадает с центральной осью стержня.
Применяя метод сечений, можно определить величину продольной силы в рассматриваемом поперечном сечении как алгебраическую сумму всех внешних сил, приложенных к стержню по одну сторону от сечения. При этом сила считается положительной, если она направлена от сечения и вызывает деформацию растяжения и отрицательной, если она направлена к сечению и вызывает деформацию сжатия.
Для определения необходимых размеров поперечного сечения стержня используем условие прочности при центральном растяжении (сжатии):
 .
.
Принимаем допускаемое напряжение на сжатие равным допускаемому напряжению на растяжение. В этом случае условие прочности принимает следующий вид:
 ,
,
где | Nmax | – максимальная величина продольной силы по модулю; S – площадь поперечного сечения.
Тогда:  .
.
Зная площадь поперечного сечения можно определить и его размеры:
а) для круга – диаметр  ;
;
б) для квадрата – сторону квадрата  ;
;
в) для прямоугольника S = b·h. Если соотношение b / h = 0,4, заменяя b = 0,4· h, получим S = 0,4 ·h2, тогда  .
.
Полученные размеры d, c, b и h округляем в большую сторону до целого числа.
Для определения величины абсолютной упругой деформации стержня используем зависимость:
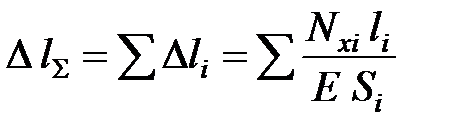 ,
,
где Nxi – величина продольной силы на i -м участке стержня; li – длина i -го участка стержня; Е – модуль упругости первого рода (модуль Юнга) – постоянная величина для каждого материала (для сталей Е = 2·105 МПа); Si – площадь поперечного сечения участка стержня с учетом полученных округленных значений d, с, b и h.




