Выбор более точной шкалы путем сравнения величин относительной устойчивости измерения

 

 

 

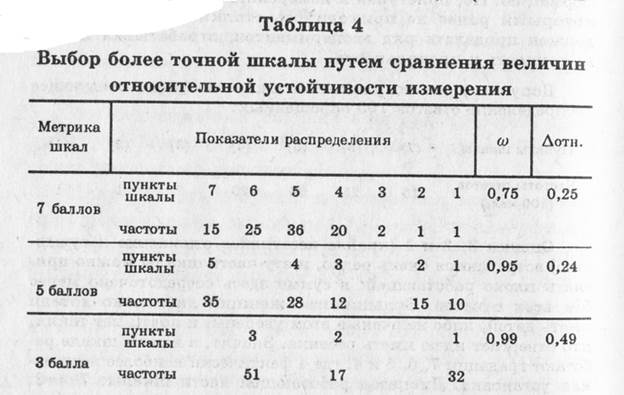
Но относительные ошибки при условии, что все градации обеих шкал работают, таковы:

для пятичленной ∆отн =0,95/(5-1)=0,238 и для трехчлен­ной ∆0,99/(3-1)=0,495; округленно 0,24 и 0,49. Получаем, что относительные ошибки семичленной шкалы (0,25) и пяти­членной (0,24) практически одинаковы, а трехчленной — существенно выше (0,49).

Какая из трех шкал более надежна? Вопрос решается при сравнении устойчивости шкалы и величины относительной ошибки. Устойчивость данных по пятичленной и трехчленной шкалам сопоставима: 95% и 99%. Иными словами, опра­шиваемые хорошо различают градации этих шкал, лучше, чем в семичленной шкале: там устойчивость равна 75%. По этой причине последнюю надо забраковать. Остается выбор из двух оставшихся. Пятичленная шкала имеет высокую устойчивость и небольшую ошибку, а трехчленная — более высокую устой­чивость и приемлемую ошибку (меньше половины градации шкалы). Но в отиошеняи к трем градациям это составит 0,49:3=0,16, а для пятичленной — 0,24:5=0,05 длины шкалы. Следовательно, пятичленная шкала втрое чувствительнее, а значит, правильнее и точнее.

Суммируем все сказанное о проверке надежности шкал в следующей схеме (схема 6).

 

 

ОБЩАЯ ХАРАКТЕРИСТИКА ШКАЛ

Применяют различные классификации измеритель­ных эталонов. Мы будем пользоваться наиболее распро­страненной — континуальной классификацией (схе­ма 7), в которой шкалы упорядочены по мере повыше­ния их способности удовлетворять требованиям более многообразных операций с числами.¹¹

¹¹ О типах шкал более подробно см. [112, 129]

 

Здесь выделено пять классов шкал, причем назва­ния классов часто двоякие: более полные и сокращен­ные. Часто шкалам даются "собственные" имена по фа­милии изобретателя (например, шкалы Гуттмана, Тер­стоуна, Гилфорда, Богардуса, Лайкерта и др.), но все они укладываются в предложенную классификацию. Далее следует запомнить, что все эти шкалы предназначены для квантификации одномерных распределений, т. е. из­мерения некоторой протяженности в одном и только в одном континууме свойств. Фактически же нередко пользуются многомерными измерениями, моделирующи­ми объект (см. гл. 5, § 1).

 

Простая номинальная шкала

 

Номинальная шкала служит предпосылкой всех шкальных процедур. Она устанавливает отношения ра­венства между явлениями, которые включены в один класс. Пункты шкалы — эталоны качественной класси­фикации свойств. Например, (А) рабочие ручного труда, не требующего специальной подготовки; (В) рабочие ручного труда высокой квалификации; (С) рабочие, за­нятые на механизированном оборудовании, средней квалификации; (D) рабочие механизированного труда высокой квалификации; (Е) автоматчики без навыков наладки; (F) пул ьтовики-наладчики.

В этой шкале, каждому из пунктов которой дается детальная эмпирическая интерпретация (по индикато­рам конечного перечня соответствующих профессий), интуитивно угадывается некоторый порядок: группы рабочих перечислены по мере повышения механизации труда и, возможно, по мере роста квалификации. Однако интуиция — не доказательство. Шкала остается неупо­рядоченной.

Более явный пример — группировка по мотивам увольнения с работы: (а) не устраивал заработок; (b) не­удобная сменность; (с) плохие гигиенические условия труда; (d) неинтересная работа и т. д. Упорядочить эти пункты невозможно: они не располагаются в контину­ум. Символическая запись номинальной неупорядочен­ной шкалы такова:

(А) ^ (В) ^ (С) ^... ^ (К), где знак ^ означает дизъюнкцию (либо—либо).

Операции с числами для номинальной шкалы сле­дующие.

1. Нахождение частот распределения по пунктам шкалы с помощью процентирования или в натуральных единицах. Нетрудно подсчитать численность каждой группы и отношение этой численности к общему ряду распределения (частоты).

2. Поиск средней тенденции по модальной частоте. Модальный (Мо) называют группу с наибольшей чис­ленностью.

Эти две операции (1) и (2) уже дают представление о распределении социальных характеристик в количе­ственных показателях. Его наглядность повышается отображением в диаграммах (рис. 6, где А — модальная группа). Во всех трех случаях за 100% принята общая численность обследованных. Диаграмма 6, а позволяет, однако, отразить распределения, в которых сумма про­центов превышает 100, т. е. некоторые обследуемые мо­гут попасть в несколько секций шкалы одновременно (например, совмещают различные виды деятельности).

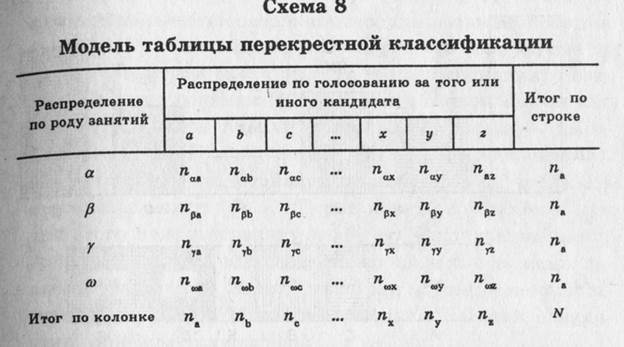
3. Самым сильным способом количественного ана­лиза является в данном случае установление взаимо­связи между рядами свойств, расположенных неупоря­доченно. С этой целью составляют перекрестные табли­цы (схема 8).

Помимо простой процентовки, в таблицах перекрест­ной классификации можно подсчитать критерий сопря­женности признаков по Пирсону: хи-квадрат (х²) — простейший показатель обоснованности вывода о наличии или отсутствии связи между сопоставляемыми характери­стиками, т. е. связанности качественных классификаций. Коэффициент Чупрова (Т-коэффициент) позволит по той же таблице определить напряженность связи, если хи-квадрат показывает, что она имеет место.¹²

¹² Об использовании различных коэффициентов при работе с неупорядоченными номинальными шкалами см. [218, С. 189—172, 189—199]. Интересен метод, предложенный С. В. Чесноковым, который позволяет анализировать данные, фиксированные в номинальных шка­лах, используя относительно "естественный" язык представления ре­зультатов, хорошо доступных неспециалистам [285].