Математика. 9 класс. Вариант 2
Часть 1
1 Найдите значение выражения 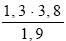
2 Фирма «Связь» выпустила в продажу две новые модели телефонов –
 модель А и модель В. На графиках показано, как эти модели
модель А и модель В. На графиках показано, как эти модели
продавались в течение года. (По горизонтальной оси откладывается
время, прошедшее с начала продаж – в месяцах, а по вертикальной —
число телефонов, проданных за это время – в тыс. шт.).
На сколько телефонов модели А было продано больше, чем телефонов модели В за
первые 8 месяцев года? Ответ дайте в тыс. штук.
3 Из объявления фирмы, проводящей обучающие семинары: «Стоимость участия в
семинаре — 3000 р. с человека. Группам от организаций предоставляются скидки:
от 5 до 10 человек — 5%; более 10 человек —8%». Сколько рублей должна
заплатить организация, направившая на семинар группу из 8 человек?
4 На координатной прямой отмечено число a. Какому из отрезков принадлежит
число a?

1) [−5; −4] 2) [−4; −3] 3) [−3; −2] 4) [3; 4]
5 Какому из данных выражений равно произведение 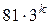 ?
?
 1)
1) 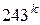 2)
2) 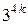 3)
3) 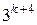 4)
4) 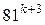
6 При проектировании торгового центра запланирована
постройка эскалатора для подъёма на высоту 4,5 м
под углом 300 к горизонту.
Найдите длину эскалатора (в метрах).
 7 Решите уравнение
7 Решите уравнение 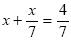
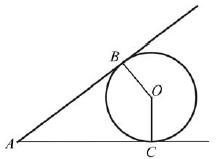
8 Окружность с центром O касается сторон
угла с вершиной A в точках B и C.
Найдите Ð BAC, если Ð BOC =127°.
Ответ дайте в градусах. Единицы
измерения в ответе не указывайте.
9 Площадь любого выпуклого четырехугольника можно вычислять по
формуле 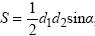 , где d 1, d 2 - длины его диагоналей, а α угол между
, где d 1, d 2 - длины его диагоналей, а α угол между
ними. Вычислите sin α, если S = 21, d 1 = 7, d 2 = 15.
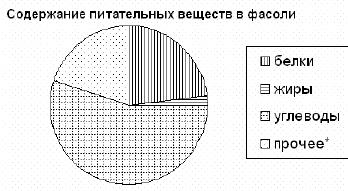
10 На диаграмме показано содержание питательных веществ в фасоли. Определите
по диаграмме, содержание каких веществ превосходит 50%.
(* – к прочему относятся вода, витамины и минеральные вещества.)
1) Белки
2) Жиры
3) Углеводы
4) Прочее
11 В таблице представлены результаты четырёх стрелков, показанные ими на
тренировке. Тренер решил послать на соревнования того стрелка, у которого
относительная частота попаданий выше. Кого из стрелков выберет тренер? В
ответе укажите номер спортсмена.

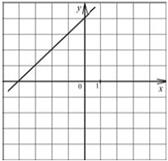
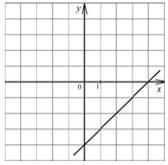
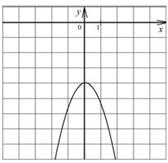
12 Для каждой функции, заданной формулой, укажите её график.
А) y = 2 x2 − 4 Б) y = x − 4 В) y = x + 4
 1) 1)
| 2)
|
3)
| 4)

|
13 Путь от посёлка до железнодорожной станции пешеход прошёл за 3 ч, а
велосипедист проехал за 1,2 ч. С какой скоростью (в км/ч) ехал велосипедист,
 если его скорость на 9 км/ч больше
если его скорость на 9 км/ч больше
скорости пешехода?
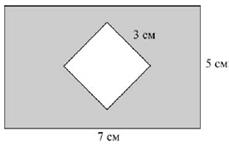
14 Из прямоугольника со сторонами 5 см и
7 см вырезали квадрат со стороной 3 см.
Найдите площадь оставшейся фигуры.
Ответ дайте в см2.
15 Укажите в ответе номера верных
утверждений.
1) Если в четырёхугольнике диагонали перпендикулярны, то этот
четырёхугольник – ромб.
2) Если при пересечении двух прямых третьей накрест лежащие углы равны, то
прямые параллельны.
3) Если гипотенуза и острый угол одного прямоугольного треугольника
соответственно равны гипотенузе и углу другого прямоугольного
треугольника, то такие треугольники равны.
4) Если расстояние между центрами двух окружностей меньше суммы их
радиусов, то эти окружности касаются.
 5) В любую трапецию можно вписать
5) В любую трапецию можно вписать
окружность.
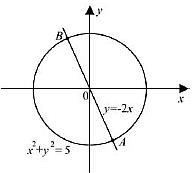
16 Окружность, изображённая на рисунке,
задаётся уравнением 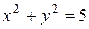 , а прямая
, а прямая
уравнением y = −2 x. Вычислите координаты
точки A.
17 Упростите выражение 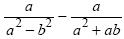 и
и
найдите его значение при 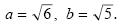
18 Решите неравенство 5 x − 2(4 − 2 x) > 4 x + 9.
Часть 2
При выполнении заданий 19–23 используйте отдельный лист (бланк). Сначала укажите номер задания, а затем запишите его решение.
19 Найдите значение выражения 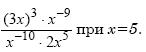
20 В параллелограмме проведены биссектрисы противоположных углов. Докажите,
что отрезки биссектрис, заключенные внутри параллелограмма, равны.
21 Первая прямая проходит через точки (0;4,5) и (3;6). Вторая прямая проходит
через точки (1;2) и (–4;7). Найдите координаты общей точки этих двух прямых.
22 Смешав 60%-ый и 30%-ый растворы кислоты и добавив 5 кг чистой воды,
получили 20%-ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг
90%-го раствора той же кислоты, то получили бы 70%-ый раствор кислоты.
Сколько килограммов 60%-го раствора использовали для получения смеси?
23 Прямая, параллельная основаниям MP и NK трапеции MNKP, проходит через
точку пересечения диагоналей и пересекает её боковые стороны MN и KP в
точках A и B соответственно. Найдите длину AB, если MP =40 см, NK =24 см.
Математика. 9 класс. Вариант 4
Часть 1
1 Найдите значение выражения 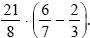
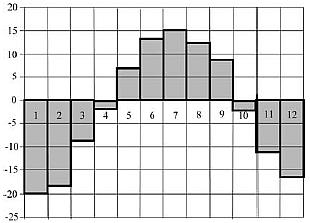
2 На диаграмме показана среднемесячная температура воздуха в Ханты-
Мансийске за каждый месяц 2003 года. По горизонтали указываются месяцы, по
вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько
было месяцев с отрицательной среднемесячной температурой.
3 Для приготовления маринада для огурцов на 1 литр воды требуется 12 г лимонной
кислоты. Лимонная кислота продается в пакетиках по 10 г. Какое наименьшее
число пачек нужно купить хозяйке для приготовления 8 литров маринада?
4 Одна из точек, отмеченных на координатной прямой соответствует числу 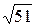 .
.
Какая это точка?
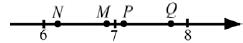
1) M 2) N 3) P 4) Q
5. Укажите выражение, тождественно равное дроби 
1) x3 2) x 3) x-7 4) x9
6 Человек, рост которого равен 1 м 70 см, стоит рядом с деревом. Найдите высоту
дерева (в метрах), если длина тени человека равна 1 м 50 см, а длина тени дерева
равна 4 м 50 см.
7 Решите уравнение (2 x + 7)(x − 1) = 0
8 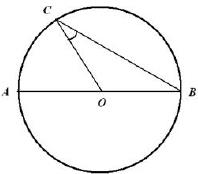 Отрезки AВ и BC являются соответственно
Отрезки AВ и BC являются соответственно
диаметром и хордой окружности с центром O.
Найдите величину угла AOC, если угол OCB
равен 29°. Ответ дайте в градусах.
Единицы измерения не указывайте.
9. Упростите выражение 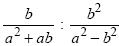 и
и
найдите его значение при 
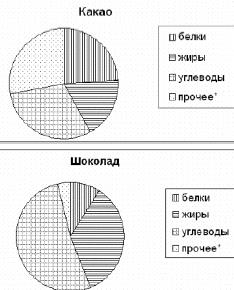
10 На диаграмме показано содержание питательных веществ в какао, молочном
шоколаде, фасоли и сливочных сухарях. Определите по диаграмме, в каком
продукте содержание жиров наибольшее.
(* – к прочему относятся вода, витамины и минеральные вещества.)
| 
|
1) Какао 2) Шоколад 3) Фасоль 4) Сухари
11 Определите вероятность того, что при бросании кубика выпало больше трёх
очков.
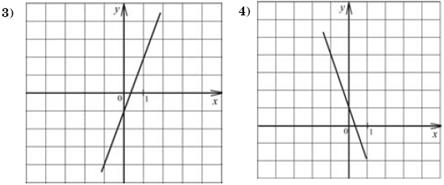
12 Для каждой функции, заданной формулой, укажите её график.
А) y = 3 x − 1 Б) y = −3 x − 1 В) y = −3 x + 1

|
|
13 Велосипедист от деревни до озера ехал со скоростью 15 км/ч, а обратно – со
скоростью 10 км/ч. Сколько часов ушло на дорогу от деревни до озера, если на
весь путь туда и обратно велосипедист затратил 5 ч?

14 Из квадрата со стороной 7 см вырезали
прямоугольник со сторонами 4 см и 5 см.
Найдите площадь полученной фигуры.
Ответ дайте в см2.
15 Укажите в ответе номера верных
утверждений.
1) Если две перпендикулярные прямые
пересечены третьей прямой, то накрест
лежащие углы равны.
2) Если в параллелограмме диагонали равны и
перпендикулярны, то этот параллелограмм – квадрат.
3) Треугольник со сторонами 1, 2, 3 существует.
4) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами
равно 1, то эти окружности пересекаются.
5) В любой ромб можно вписать окружность.
16  Окружность, изображённая на рисунке,
Окружность, изображённая на рисунке,
задаётся уравнением 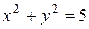 , а прямая
, а прямая
уравнением y = −2 x. Вычислите координаты
точки B.
17. Из формулы 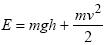 выразите
выразите
скорость v.
18 Решите неравенство 3 x − 4(2 − x) ≤ 12 x + 3
Часть 2






