¬ поштовому звТ€зку рад≥альн≥ маршрути використовуютьс€, в основному, €к маг≥стральн≥ та рег≥ональн≥ маршрути, а в раз≥ нестач≥ часу дл€ проходженн€ к≥льцевих маршрут≥в Ц також €к окружн≥ маршрути.
«адача формулюЇтьс€ так: заданий звТ€зний зважений граф, вершини €кого в≥дпов≥дають вузлам мереж≥ перевезень пошти, ребра Ц шл€хам, що зТЇднують ц≥ вузли, а ваги ребер Ц прот€жност€м в≥дпов≥дних шл€х≥в. «найти найкоротш≥ шл€хи, що зТЇднують задану початкову вершину з рештою вершин графа.
–озвТ€занн€ задач≥ засновано на формуванн≥ так званого рельЇфу графа у вид≥ ваг вершин графа, значенн€ €ких дор≥внюють значенн€м прот€жностей найкоротших шл€х≥в м≥ж ними ≥ початковою вершиною графа.
ѕочатков≥й вершин≥ ¬≥ надаЇтьс€ вага –≥ = 0, решт≥ вершин Ц неск≥нченн≥ ваги –j = ¥.
Ќа кожному кроку формуванн€ рельЇфу графа знаходитьс€ ран≥ше неперев≥рена вершина м≥н≥мальноњ ваги, в≥дносно €коњ формуютьс€ ваги тих неперев≥рених вершин, що безпосередньо зТЇднан≥ з перев≥рною вершиною. ¬ага неперев≥реноњ вершини зам≥нюЇтьс€ вагою перев≥рноњ вершини, зб≥льшеноњ на вагу ребра, що зТЇднуЇ зазначен≥ вершини, €кщо перша перевищуЇ другу.
–азом з формуванн€м рельЇфу формуЇтьс€ ≥нформац≥€ про значенн€ ваги кожноњ вершини ≥ про номер вершини, в≥д €коњ ц€ вага отримана.
Ќайкоротш≥ шл€хи формуютьс€ €к посл≥довност≥ запис≥в зазначеноњ ≥нформац≥њ, прочитан≥ в пор€дку, зворотному до њхнього формуванн€.
јлгоритм формуванн€ рельЇфу графа наведений на рис. 2.5.

ѕочаток
 |


1. ѕрисвоЇнн€ початков≥й вершин≥
ваги –i = 0, присвоЇнн€ решт≥
вершин ваг –j = 999
 | |||
 | |||
2. ¬иб≥р серед неперев≥рених вершин
графа вершини ¬k м≥н≥мальноњ ваги
 | |||
 | |||

3. ќбчисленн€ ваги 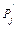 = lk + P(k,j)
= lk + P(k,j)
черговоњ неперев≥реноњ вершини
Bj графа, безпосередньо повТ€заноњ
з перев≥рною вершиною Bk
 |

Ќ≥

 4.
4. 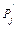 < –j
< –j
 “ак
“ак


5. –j = 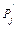 , запис Bk
, запис Bk
 |

6. ¬с≥
вершини Bj, безпосередньо Ќ≥
 повТ€зан≥ з вершиною Bk,
повТ€зан≥ з вершиною Bk,
перев≥рен≥

“ак
7. ѕрисвоЇнн€ перев≥рн≥й вершин≥
Bk позначки Уперев≥ренаФ (*)
 |

Ќ≥ 8. ѕерев≥рено
 n - 1 вершин графа
n - 1 вершин графа
 |
“ак

≥нець
–исунок 2.5. јлгоритм формуванн€ рельЇфу графа
јлгоритм м≥стить 8 блок≥в.
” блоц≥ 1 створюЇтьс€ початковий рельЇф графа. ѕочатков≥й вершин≥ ¬≥ присвоюЇтьс€ м≥н≥мальна вага –≥ = 0, решт≥ вершин графа Bj (j = 1, 2, Е n, j ¹ i) Ц неск≥нченн≥ ваги –j = ¥, €к≥ подаютьс€ €к надм≥рн≥ ваги –j = 999.
” блоц≥ 2 серед неперев≥рених вершин вибираЇтьс€ вершина ¬k м≥н≥мальноњ ваги –k.
” блоц≥ 3 обчислюЇтьс€ вага 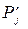 = –k + –(k,j) черговоњ неперев≥реноњ вершини Bj в≥дносно перев≥рноњ вершини Bk, що безпосередньо повТ€зана з вершиною Bj графа.
= –k + –(k,j) черговоњ неперев≥реноњ вершини Bj в≥дносно перев≥рноњ вершини Bk, що безпосередньо повТ€зана з вершиною Bj графа.
” блоц≥ 4 обчислена вага 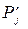 пор≥внюЇтьс€ з вагою –j вершини Bj. ѕри
пор≥внюЇтьс€ з вагою –j вершини Bj. ѕри 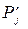 < –j виконуЇтьс€ перех≥д до блоку 5, при
< –j виконуЇтьс€ перех≥д до блоку 5, при 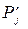 ³ –j Ц до блоку 6.
³ –j Ц до блоку 6.
|
|
|
” блоц≥ 5 вага –j зам≥нюЇтьс€ вагою 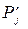 , тобто значенн€ ваги вершини Bj знижуЇтьс€, ≥ запамТ€товуЇтьс€ вершина Bk, в≥д €коњ одержано значенн€ ваги –j.
, тобто значенн€ ваги вершини Bj знижуЇтьс€, ≥ запамТ€товуЇтьс€ вершина Bk, в≥д €коњ одержано значенн€ ваги –j.
” блоц≥ 6 перев≥р€Їтьс€, чи вс≥ вершини ¬j графа, безпосередньо повТ€зан≥ з перев≥рною вершиною Bk, перев≥рен≥. якщо так Ц зд≥йснюЇтьс€ перех≥д до блоку 7, €кщо н≥ Ц поверненн€ до блоку 3.
” блоц≥ 7 перев≥рн≥й вершин≥ Bk присвоюЇтьс€ позначка Уперев≥ренаФ (*) ≥ вона виключаЇтьс€ з подальшого розгл€ду.
” блоц≥ 8 перев≥р€Їтьс€ к≥льк≥сть вершин графа, що вже перев≥рен≥. якщо таких вершин менше n - 1 Ц зд≥йснюЇтьс€ поверненн€ до блоку 2, ≥ процес формуванн€ рельЇфу графа повторюЇтьс€, €кщо њх n - 1 Ц рельЇф графа сформований ≥ робота алгоритму зак≥нчуЇтьс€.
јлгоритм формуванн€ найкоротших шл€х≥в за сформованим рельЇфом графа наведено на рис. 2.6.
јлгоритм м≥стить 5 блок≥в.
” блоц≥ 1 ф≥ксуЇтьс€ поточна перев≥рна вершина Bl = Bj (j = 1, 2, Е n,
j ¹ i).
” блоц≥ 2 виконуЇтьс€ зчитуванн€ р€дка l таблиц≥ рельЇфу графа.
” блоц≥ 3 ф≥ксуЇтьс€ значенн€ номера попередньоњ вершини Bk графа та ваги –l.
” блоц≥ 4 значенн€ l зам≥нюЇтьс€ значенн€м k, тобто поточна вершина Bl зам≥нюЇтьс€ поточною вершиною Bk графа.
” блоц≥ 5 пор≥внюютьс€ значенн€ l ≥ i. ѕри l ¹ i виконуЇтьс€ поверненн€ до блоку 2 ≥ формуванн€ шл€ху м≥ж вершинами Bi та Bj графа продовжуЇтьс€. ѕри l = i шл€х м≥ж вершинами Bi та Bj графа сформований ≥ робота алгоритму зак≥нчуЇтьс€.

ѕочаток
 |

1. l = j (j = 1, 2 Е, n, j ¹ i)
 | |||
 | |||

2. «читуванн€ р€дка l таблиц≥
рельЇфу графа
 |


3. «апис номера попередньоњ
вершини Bk графа ≥ ваги Pl
 |
4. l = k
 |

 Ќ≥ 5. l = i
Ќ≥ 5. l = i
 “ак
“ак

≥нець
–исунок 2.6. јлгоритм формуванн€ найкоротших шл€х≥в
ѕосл≥довн≥сть крок≥в формуванн€ рельЇфу графа рис. 2.3 в≥дносно вершини 4 наведено в табл. 2.3 Е 2.10 (Bi Ц будь-€ка вершина, –i Ц вага вершини Bi, * - позначка вершини Уперев≥ренаФ, Bk Ц вершина, в≥д €коњ одержана вага –i).
|
|
|
| рок 0: початковий | рок 1: –i = 0, Bi = 4 | рок 2: –i = 2, Bi = 3 | |||||||||
| Bi | * | –i | Bk | Bi | * | –i | Bk | Bi | * | –i | Bk |
| * | |||||||||||
| * | * | ||||||||||
|
|
|
|
|
|
| рок 3: –i = 3, Bi = 1 | рок 4: –i = 3, Bi = 7 | рок 5: –i = 4, Bi = 6 | |||||||||
| Bi | * | –i | Bk | Bi | * | –i | Bk | Bi | * | –i | Bk |
| * | * | * | |||||||||
| * | * | * | |||||||||
| * | * | * | |||||||||
| * | |||||||||||
| * | * | ||||||||||
|
|
|
—формован≥ найкоротш≥ шл€хи м≥ж вершиною 4 та рештою вершин графа наведено у табл. 2.11 (в дужках зазначен≥ прот€жност≥ в≥дпов≥дних шл€х≥в або њх частин)
|
| 4 (0) Ц 3 (2) Ц 1 (3) |
| 4 (0) Ц 3 (2) Ц 1 (3) Ц 2 (7) |
| 4 (0) Ц 3 (2) |
| 4 (0) Ц 6 (4) Ц 8 (6) Ц 5 (9) |
| 4 (0) Ц 6 (4) |
| 4 (0) Ц 7 (3) |
| 4 (0) Ц 6 (4) Ц 8 (6) |
Ќаведен≥ алгоритми формуванн€ рельЇфу графа (рис. 2.5) ≥ формуванн€ найкоротших шл€х≥в за сформованим рельЇфом графа (рис. 2.6) можуть бути використан≥ також дл€ формуванн€ шл€х≥в, найкоротших за числом пром≥жних вершин.
” задачах поштового звТ€зку так≥ шл€хи використовуютьс€ дл€ перевезень важкоњ (посилочноњ) пошти з метою скороченн€ витрат, повТ€заних з њњ перевантаженн€м у транзитних вузлах.
ƒл€ одержанн€ зазначених шл€х≥в достатньо прийн€ти ваги ус≥х ребер графа р≥вними одиниц≥.
” табл. 2.12 Е 2.18 наведена посл≥довн≥сть крок≥в формуванн€ рельЇфу графа рис. 2.3 в≥дносно вершини 4 за умови р≥вност≥ ваг ус≥х його ребер одиниц≥ (позначенн€ Ц так≥ ж сам≥, що в табл. 2.3 Е 2.10).
|
|
|
| рок 0: початковий | рок 1: –i = 0, Bi = 4 | рок 2: –i = 2, Bi = 3 | |||||||||
| Bi | * | –i | Bk | Bi | * | –i | Bk | Bi | * | –i | Bk |
| * | |||||||||||
| * | * | ||||||||||
|
|
|
|
|
|
| рок 3: –i = 3, Bi = 1 | рок 4: –i = 3, Bi = 7 | рок 5: –i = 4, Bi = 6 | |||||||||
| Bi | * | –i | Bk | Bi | * | –i | Bk | Bi | * | –i | Bk |
| * | * | * | |||||||||
| * | * | * | |||||||||
| * | * | * | |||||||||
| * | * | ||||||||||
| * | |||||||||||
 |
ќск≥льки на кроц≥ 6 вс≥ вершини отримали ваги, формуванн€ рельЇфу зак≥нчуЇтьс€.
” табл. 2.19 наведено найкоротш≥ за числом пром≥жних вершин шл€хи м≥ж вершиною 4 та рештою вершин графа.
|
| 4 Ц 1 |
| 4 Ц 1 Ц 2 |
| 4 Ц 3 |
| 4 Ц 1 Ц 2 Ц 5 |
| 4 Ц 6 |
| 4 Ц 7 |
| 4 Ц 6 Ц 8 |






