Балансовый анализ отвечает на вопрос макроэкономики: каким должен быть объем производства каждой из n-отраслей экономической системы, чтобы удовлетворить все потребности в данном продукте.
Часть экономики, состоящая из двух отраслей – металлургия и энергетика.
| Производство | потребители | потребление | Валовый выпуск | |
| м | э | |||
| М | ||||
| э |
Это таблица баланса
В этой таблице в каждой строке приведены объемы производства (в млрд рублей) каждого вида продукции, производимой соответствующей отраслью и распределение этой продукции для потребления каждой отраслью и для внешнего потребления.
В частности:
М производит продукции на 100 млрд, из них 5 млрд – самой этой отраслью расходуется, 20 – энергетикой, 75-внешнее потребление.
Сама М, как потребитель, расходует 5 млрд своей отрасли и 15 млрд продукции Э.
Разделив первые 2 столбца на объем производства соответствующей отрасли получаем структурную матрицу (матрицу Леонтьева):
А=
А=(aij) прямые затраты продукции отрасли i на 1 рубль производства отрасли j.
0,40р отрасли М на производство 1р отрасли Э.
Допустим, что весь производственный сектор разбит на n-отраслей, которые производят однородный продукт
вектор валового выпуска отраслей:
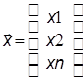
|  Вектор конечного потребления
|
Уравнение межотраслевого баланса
x1=a11*x1+a12*x2+a1n*xn+d1
x2=a21*x1+a22*x2+a2n*xn+d2
Основную задачу межотраслевого баланса можно сформулировать:
Зная матрицу Леонтьева А и объем конечного потребления
найти планируемые объемы валового выпуска X всех отраслей народного хозяйства.
Осн. результат 
межотраслевого баланса, где d – вектор конечного потребления, x – вектор валового выпуска.
x и d – векторы с неотрицательным компонентом
Модели линейного программирования.
МОДЕЛИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ — математические модели решения экономических задач, представленные в форме задач линейного программирования. Целевая функция, связи и ограничения в такой модели выражены в виде линейных соотношений.
МОДЕЛИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задача оптимального распределения ресурсов
Построение математической модели
Общий вид задачи оптимального распределения ресурсов
Варианты задачи оптимального распределения ресурсов
Транспортная задача.
Транспортная задача - задача о поиске оптимального распределения поставок однородного товара от поставщиков к потребителям при известных затратах на перевозку (тарифах) между пунктами отправления и назначения. Является задачей линейного программирования специального вида.
Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку).
Решение транспортной задачи можно решить:
· методом северо-западного угла
Допустимое (но не всегда оптимальное с точки зрения стоимости доставки) начальное решение транспортной задачи можно построить, последовательно перебирая строки таблицы (то есть поставщиков) сверху вниз. В пределах каждой строки, нужно перебрать слева направо не охваченных или не полностью охваченных поставками потребителей, записывая в соответствующие ячейки объем поставляемого груза от поставщика в данной строке, и так до исчерпания возможностей поставщика. Таким образом, весь груз от поставщиков будет распределен по потребителям. Этот метод был предложен Данцигом в 1951 г. и назван Чарнесом и Купером «правилом северо-западного угла».
· методом наименьшего элемента (минимальных тарифов)
Записывать отгрузки в первую очередь в те ячейки, где тариф минимален. Этот метод позволяет получить более приближенное к оптимальному решение, которое, однако, может потребовать дальнейшей оптимизации. Метод минимальных тарифов с его модификациями (минимальный тариф по строке или минимальный тариф по столбцу) был описан Данцигом в работе 1951 г.
· методом Фогеля
· Метод потенциалов позволяет за несколько шагов (итераций) найти полностью оптимальное решение транспортной задачи. Перед решением задачи этим методом нужно найти допустимое начальное решение одним из методов, описанных в выше.
