Вопросы к экзамену по математике-1
1. Множества, операции над множествами.
2. Числовая прямая, подмножества числовой прямой. Окрестности.
3. Границы числовых множеств.
4. Отображения и функции.
5. Основные элементарные функции, их графики. Элементарные и неэлементарные
функции.
6. Точка сгущения. Определение предела функции на языке окрестностей. Графическая
иллюстрация. Различные случаи.
7. Односторонние пределы, графическая иллюстрация. Теорема об односторонних пределах.
8. Предел функции на языке ε-δ. Предел последовательности на языке ε-δ. Предел функции по Гейне.
9. Бесконечно малая функция. Основная теорема анализа. Бесконечно большая функция,
связь с бесконечно малой.
10.Теоремы о бесконечно малых функциях.
11. Основные теоремы о пределах.
12. Сравнение бесконечно малых. Символы О и о. Эквивалентность, теоремы об
эквивалентных бесконечно малых.
13. Замечательные пределы. Эквивалентные пары. Порядок функций.
14. Непрерывность функции в точке – основное определение, определения на языке
окрестностей и ε-δ.
15. Приращение функции в точке. Разностное определение непрерывности. Непрерывность
на множестве. Односторонняя непрерывность.
16. Теоремы о непрерывных функциях – непрерывность арифметических операций, сложной и
обратной функций, основных элементарных и элементарных функций.
17. Теоремы о функциях, непрерывных на замкнутом промежутке – о сохранении знака,
о промежуточном значении, о корне функции, 1-я и 2-я теоремы Вейерштрасса. Примеры.
18. Точки разрыва, их классификация. Примеры.
Определение производной функции в точке.
Правила дифференцирования – производная суммы, разности, произведения,
Частного, сложной функции, логарифмическое дифференцирование.
20. Связь между непрерывностью и дифференцируемостью. Односторонние производные.
21. Геометрический смысл производной. Графическая иллюстрация дифференцируемых и
не дифференцируемых в точке функций. Уравнения касательной и нормали.
22. Дифференцируемость функции в точке. Дифференциал функции. Основная теорема.
Геометрический смысл дифференциала и применение для приближенных вычислений.
23. Дифференцирование обратной и неявно заданной функций.
24. Параметрическое задание функций, их дифференцирование.
25. Примеры функций, заданных параметрически. Параметрические уравнения прямой,
Окружности, эллипса, гиперболы, циклоиды, астроиды.
26. Гиперболические и обратные гиперболические функции, их дифференцирование.
27. Производные высших порядков. Формула Лейбница.
28. Дифференциалы высших порядков. Основное отличие от дифференциала первого
порядка.
Теоремы Ферма и Ролля.
30. Теоремы Лагранжа и Коши. Формула конечных приращений.
31. Правило Лопиталя-Бернулли. Различные случаи.
32. Сравнение скорости роста многочлена, экспоненты, логарифма при 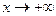 .
.
Многочлен Тэйлора, его основное свойство.
34. Формула Тэйлора и ее основное применение. Формула Маклорена.
35. Остаточный член в форме Пеано. Запись приращения функции с помощью формулы
Тэйлора.






