Задания для самостоятельной работы
Задание 1
Основные понятия теории множеств. Отношения на множествах
1) Даны множества А – «множество различных букв слова ФИЛОЛОГИЯ» и В – «множество гласных букв русского алфавита».
а) запишите множества А и В с помощью перечисления элементов;
б) найдите объединение, пересечение, разность, симметрическую разность множеств А и В.
2) Найдите булеан множества Е – «множество согласных букв в слове АЛФАВИТ»
3) Найдите… а) декартовое произведение множеств Е (из 2) и К={0,1}; б) декартовый квадрат множества Е.
4) 
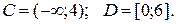Выполните над множествами С и D операции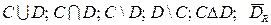 
5) Докажите с помощью кругов Эйлера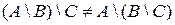 
6) Перечислите свойства бинарных отношений и укажите их тип:
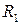={иметь большую среднюю длину словоформ} на множестве языков мира;
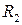={принадлежать к одной языковой группе};
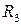={ быть знакомым} на множестве людей.
Дополнительные задания:
7) Задайте тремя способами на множестве букв {А, Д, Е, Л, М} отношение R=«занимать более высокую строчку в русском алфавите».
8) Найдите множество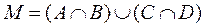 
, если
Задание 2:
Элементы комбинаторики.
1. Сколько 3-х буквенных серий для автомобильных номеров можно составить из 30 букв русского алфавита (исключая ь, ъ, й), если…а) буквы в серии различны, б) буквы в серии могут повторяться?
2. Каким числом способов можно выбрать 2 гласные буквы русского языка, если эти буквы…
а) различны; б) могут быть одинаковыми?
3. Сколько перестановок с повторениями можно составить из букв слова АНАГРАММА?
4. Сколькими способами можно рассадить персонажей басни И.А. Крылова «Квартет»?
5. Сколько 4-буквенных «слов» можно составить из букв слова «СЛОВАРЬ», если на первом месте в полученном «слове» должна стоять буква «С», а на последнем – «Ь», и все буквы в «слове» различны.
Дополнительные задания:
6. В шахматном турнире было сыграно 120 игр. Сколько было участников, если каждые 2 участника встречались между собой только 1 раз?
7. Сколько анаграмм (литературный приём, состоящий в перестановке букв или звуков определённого слова (или словосочетания), что в результате даёт другое слово или словосочетание) можно получить из букв слов «ГАГАГА», «ЯЗЫК», «МАТЕМАТИКА»?
8. *Сколько палиндромов (число, буквосочетание, слово или текст одинаково читающееся в обоих направлениях) можно получить из букв слов «ГАГАГА», «ЯЗЫК», «МАТЕМАТИКА»?
Начальные понятия теории вероятностей
9. В высказывании Карла Вейерштрасса «Нельзя быть настоящим математиком, не будучи немного поэтом» 8 слов.
а) Автомат случайным образом выбирает одно из слов высказывания. Найдите вероятность событий:
А=«выбрана частица НЕ»; В= «выбран глагол»; С=«выбрано имя существительное»; К= «выбран предлог»; М= «выбрано любое из 8 слов данного высказывания».
б) Автомат случайным образом выбирает два слова данного высказывания. Найдите вероятность событий:
D= «Оба выбранных слова начинаются с буквы Н»
Е=«Одно слово – глагол, а другое – имя существительное».
Задание 3:
