Методи оцінки медичної інформації

Особливістю медицини і біології є вар’ювання кількісних показників організму, залежність їх від багатьох факторів.

Рядом розподілу називають впорядкований перелік варіюючих властивостей. Аналіз розподілу варіюючих властивостей та явищ дозволяє медикові приймати рішення про тер­міни ізоляції інфекційних хворих, тривалість лікування, зробити висновки про частоту та характер можливих ускладнень і т. д. Застосування ймовірнісних оцінок до об’єктів та явиш пов'язане з закономірністю повторю­ваності, стабільністю їх розподілу (по належності до груп крові, складу білків плазми, елементів крові і т. д.).

Зручно представляти розподіли явищ або властивостей у вигляді ряду (або таблиці), графічно (гістограма, крива, полігон) або у вигляді алгебраїчного виразу. Побудову ряду розподілу починають з групування експериментальних даних за певним значенням признака, на основі ретельної оцінки числа інтервалів та його величини.

У практиці медичних досліджень найбільш часто для характеристики розподілу використовують наступні узагальнюючі числові характеристики.

Середнє арифметичне:

,

де n — число (об’єм) досліджуваної сукупності; х_і — варіанти, значення величин.

Особлива властивість 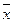— сума відхилень від цієї величини окремих варіант (в “+” або “–”) дорівнює 0, а сума квадратів цих відхилень від середньої величини менша, ніж сума квадратів відхилень від довільної іншої варіанти.

Середнє квадратичне (стандартне) відхилення:

,

характеризує розсіювання, відхилення від середньої величини ряду, а s² називають дисперсією ряду розподілу.

Графічні методи зображення рядів розподілу зручні для ілюстрації аналізу експериментальних даних — до них належить побудова гістограм та полігонів розподілу випадкових величин.

Нехай маємо деяку випадкову величину Х, яка в результаті n вимірів приймає неперервний ряд значень. Отримані результати можна представити наочно, побудувавши діаграму, яка показує, як отримувались при вимірах ті або інші значення Х. Для цього весь діапазон виміряних значень, відкладених по осі Х, розбивають на рівні інтервали, шириною DХ. Потім підраховують число m значень виміряної величини, які попали в кожен інтервал, і на кожному інтервалі будують прямокутник з основою, рівною ширині інтервалу, і висотою, рівною числу значень вимірюваної величини, які потрапили в даний інтервал.

Рис.1. Гістограма.

В результаті отриму­ється даграма (рис. 1), яку називають гістограмою. Площа кожного прямокутника дорівнює частоті признака для даного інтервалу Гістограму можна побудувати інакше: по осі у відкладати m/n — тобто відносне число значень Х, що попали в інтервал DХ.

 

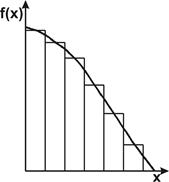Рис.2. Крива розподілу випадкової величини.

Така гістограма на вигляд подібна до розглянутої (рис.1). Якщо число вимірів n велике, а Dх дуже мале, то в границі замість гістограми отримують плавну криву (рис. 2), яка характеризує долю повного числа вимірів випадкової величини, значення якої попадають у кожен інтервал. Така крива називається кривою розподі­лу випадкової величини, а

 

функція у = f(х), що описує цю криву, — густиною ймовірності даного розподілу даної величини.

Полігон розподілу — має варіанти по осі абсцис та абсолютні значення частот по осі ординат. Точки перетину відповідних координат з'єднують прямими лініями (рис. 3).

В медицині часто бувають випадки, коли лише при дос­лідженні множини випадкових і незалежних подій проявляється закономірність, притаманна досліджуваній події вцілому. Чим більше буде виконано дослідів, тим стійкішою буде частота — ймовірність прояву певної події.

Багатогранність і випадковість більшості явищ і процесів в медицині та охороні здоров’я зумовлюють застосування до них теорії ймовірностей для встановлення законів їх розподілу та подальшій математичній обробці на ЕОМ, а також моделювання з допомогою засобів сучасної обчислювальної техніки.

Аналіз ряду розподілу чисельностей (таблиць або гістограм) дає ряд ймовірностей можливих значень випадкової величини.

 

Рис. 3. Полігон розподілу.

В медицині та біології розподіли чисельностей різноманітні, однак частіше інших їх можна співставити з одним із основних теоретичних розподілів: розподілом по­казників, який характеризує частоту признака або явища — так званим біноміальним розподілом (розподіл Бернуллі або

розподіл Пуассона — для дуже рідкісних явищ), і розподілом величин біологічних об’єктів, інтенсивність їх властивостей і результатів вимірів — законом так званого нормального розподілу (роз­поділ Гаусса). Як розподіл Бернуллі, так і розподіл Пуассона, застосовують у випадку дискретних випадкових величин (що приймають в певному інтервалі лише цілочисельні значення).

Числовими характеристиками дискретних випадкових величин є:

а) ймовірність Рі того, що випадкова величина прийме значення хі;

б) математичне сподівання М випадкової величини (се­ре­днє значення), під яким розуміють суму добутків всіх можливих значень випадкової величини на ймовірність цих значень:

.

в) дисперсія або середнє квадратичне відхилення - рівна сумі квадратів відхилень окремих значень хі випадкової величини х від її математичного очікування М:

.

Числові характеристики неперервних випадкових величин будуть розглянуті пізніше.

Біологічні об’єкти відрізняються різноманітністю властивостей для однорідної сукупності об’єктів. Часто виявляється певний зв’язок між варіаціями за різними ознаками. Наприклад, чим більший ріст людини, тим біль­ша її вага.

Кореляційною або статистичною називають залежність, при якій зміна однієї величини веде до зміни розподілу іншої.

Лініями регресії називають графічні представлення корелюючих ознак.

 

Лабораторна робота № 1