Порядок проведения математического боя
Эту игру лучше проводить в учебное время (3-4 ч.решения,2ч-бой)
Количество участников в командах одинаково. Заранее устанавливается точное начало боя.
Пометка участника игры
1. Каждый или команды выходит к доске не более 2х раз не зависимо от роли.
2. Число минутных перерывов для каждой команды не более 3х.
3. Времени на доклад не более 15 минут, после которого жюри решают дать еще 1раз докладчику или передать слово оппоненту.
4. Если оппонент не нашел пробелов в решении докладчика, то жюри не разрешает предложить ему свое решение.
5. Заранее оговаривается круг фактов и методов, которые можно использовать при решении задач, не входящие в школьную математику.
6. На первом этапе можно использовать литературу и калькуляторы.
7. Во время доклада и оппонировании нельзя использовать записанные ранее решения.
8. Ничья в игре присуждается, если разница очков не более 3х.
Решения задач
Одновременно жюри предлагает командам список задач, которые они решают в разных кабинетах. Председатель жюри регулярно посещает команды и отвечает на вопросы по содержанию, при этом каждое уточнение, данное 1 команде должно сообщаться и другой. Жюри не имеет права давать информацию о трудности заданий и количестве задач, решенных соперниками. Задач должно быть четное количество(8-10).
Начало боя
К назначенному времени команды и жюри собираются вместе в одном кабинете. Целесообразно создать учебную обстановку для общения.

Капитаны сообщают название команды. На доске изображена таблица результатов.
| Очки жюри | Зайцы | Очки | Вызов | Очки | Волки | ||
| Петрова |

| Иванов |
Существует ограничение на общение участников.
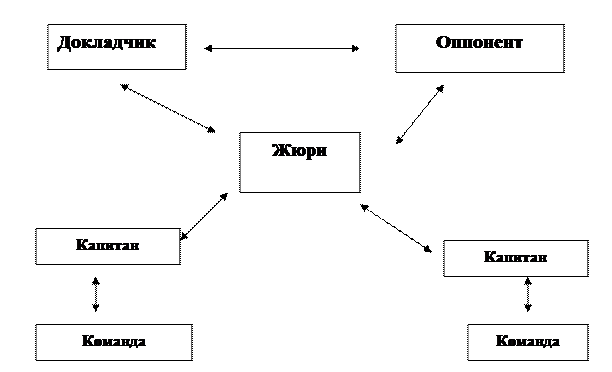
Бой начинается с конкурса капитанов для выяснения 1 вызова. Капитанам предлагается простая задача. Конкурс заканчивается, когда один из капитанов дает ответ. Если ответ верный, побеждает тот, кто его дал, если не верный присваивается победа другому команде. Капитан, победивший в конкурсе сообщает какая команда будет вызываться.
Вызов
Капитан, вызывающей команды, называет № задачи: «Вызываем команду соперников на решение задачи №…..». Капитан 2ой команды, посоветовавшись внутри команды может ответить: «Вызов принят. Докладчик Иванов». Тогда 1я команда определяет оппонента «проверка корректности». Тогда вызывавшая команда выставляет докладчика, а другая оппонента.
Докладчик и оппонент
Докладчик сообщает решение, его сообщение заканчивается словами: «Доклад закончен». Затем оппонент задает вопросы (если есть) и соглашается или не соглашается с решением. «С решением согласен» или «С решением не согласен частично», или «С решением не согласен полностью». Затем жюри задает вопросы докладчику, затем оппоненту, если он не полностью соглашается с решением.
Начисление очков
Каждая задача стоит 12 очков. Эти очки распространяются между докладчиком и оппонентом и жюри. За чистое решение задачи дается 12 очков, за полное оппонирование – 6 очков. Оппонент получает очки за те вопросы по решению на которые докладчик не смог ответить. Если оппонент указал на существенные пробелы, которые затем докладчик исправил, то оппонент может получить до 2х очков. За красивое решение или оппонирование жюри может добавить 1 премиальное очко, которое не входит в сумму очков. После решения и оппонирования жюри выставляет баллы и объясняет, за что они даны или сняты. Жюри достается остаток баллов до 12 от суммарного балла 2х команд.
О формировании команд
Входит от 6-12 человек. Команды могут быть разновозрастные или сформированы из учеников одного класса.
Фрагмент урока.
Конкурс капитанов – 5 баллов. Время – 1 минута.Переложив 4 спички, превратите топор в три равных треугольника.

ОТВЕТ:

Задание.
1)Даны 16 чисел 1, 11, 21, 31 и так далее (каждое следующее на 10 больше предыдущего). Можно ли расставить их в таблице 4´4 так, чтобы разность любых двух чисел, стоящих в соседних по стороне клетках делилась на 4.
Ответ1. Нельзя. Разность двух чисел делится на 4 тогда и только тогда, когда числа имеют одинаковый остаток от делении на 4. Поэтому, чтобы выполнялось требование в условии задачи, необходимо, чтобы все числа в таблице имели одинаковый остаток от деления на 4. Но среди 16 данных чисел 8 при делении на 4 дают остаток 1, остальные – остаток 3.
2) В треугольнике АВС биссектриса АЕ равна отрезку СЕ. Найдите угол АВС, если АС=2АВ.
Ответ2. Проведем высоту ED D AEC. D AEC – равнобедренный, следовательно, ED является медианой. Т.к. АС=2АВ, то AD=DC=АВ. D AED = D АВЕ по двум сторонам и углу между ними. Отсюда ÐАВЕ=ÐАDE=90°.
 3) Два игрока по очереди берут по одной цифре из общего для них набора
3) Два игрока по очереди берут по одной цифре из общего для них набора
0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Выигрывает тот, кто первым сможет из взятых им цифр при помощи
знаков арифметических действий составить выражение, равное 14.
Ответ3. Выиграет первый. Одна из многих возможных выигрышных стратегий первого такова. Первым ходом он берет число 7. Второй в ответ вынужден брать двойку (иначе ее возьмет первый и выиграет: 2´7 = 14). Тогда первый берет единицу и создает сразу две угрозы: 17 – 3 и 1 + 7 + 6. Поскольку взять одновременно тройку и шестерку второй своим вторым ходом не может, первый третьим ходом возьмет одну из этих цифр и выиграет. Своим вторым ходом второй выиграть не может, ибо из двойки и любой другой цифры, как легко проверить, число 14 получить нельзя.
4) Имеется 555 гирь весом 1 г, 2 г, 3 г, …, 555 г. Разложить их на три равные по весу кучи.
Ответ4.
I кучка II кучка III кучка
555 554 553
550 551 552
549 548 547
544 545 546
…………………………
15 14 13
10 11 12
Будем раскладывать гири по 6 штук, как указано в схеме. После разложения каждых 6 гирь вес кучек окажется равным. Оставшиеся 9 гирь разложим следующим образом: 1, 9, 5; 2, 6, 7; 3, 4, 8.
5) Малыш и Карлсон поочередно берут конфеты из одного пакета. Малыш берет одну конфету, Карлсон – две, затем Малыш берет три конфеты, Карлсон – четыре, и так далее. Когда количество оставшихся в пакете конфет станет меньше необходимого, тот, чья очередь наступила, заберет все оставшиеся конфеты. Сколько конфет было в пакете первоначально, если у Малыша в итоге оказалась 101 конфета?
Ответ5.
1+3+5+7+9+ … +19=(1+19)+(3+17)+ … +(9+11)=20´5=100. Предпоследним ходом Малыш взял 19 конфет, последним – одну. Карлсон взял 2+4+ … +20 = 22´5=110 конфет, всего было 211 конфет.
6) На сторонах ВС и СD квадрата ABCD взяты точки К и L соответственно так, что ÐВАК=40°, а ÐLAD=10°. Докажите, что AL=LD+BK.
Ответ 6:
Построим D ABF=D ADL. При этом точка F будет лежать на ВК, так как ÐАВК+ÐАBF=90°+90°=180°, BF=LD, AF=AL.
ÐKAF=10°+40°=50°, ÐAKF=90°- 40°=50°, т. е. ÐKAF=ÐAKF.
Тогда DAFK – равнобедренный, и AL=AF=FK=FB+BK=LD+КВ.

7) Футбольный мяч сшит из 32 лоскутов: белых шестиугольников и черных пятиугольников. Каждый черный лоскут граничит только с белыми, а каждый белый с тремя черными и тремя белыми. Сколько лоскутов белого цвета?
Ответ 7:
Если белых лоскутов х, то имеется 3х границ между белыми и черными лоскутами. Черных лоскутов 32-х. Т. к. каждый из них граничит с 5 белыми, то число границ между белыми лоскутами и черными равно также 5(32-х). Отсюда 3х=5(32-х), х=20.
8) У звезды ABCDE равны углы при вершинах А и В, и углы при вершинах Е и С, а также равны длины отрезков АС и ВЕ. Докажите, что AD=BD.
Ответ 8: Обозначим точки пересечения отрезков BD и AD c отрезком EC через H и F соответственно. D EBH = D ACF по 2-м углам и стороне между ними. Тогда
BH=AF, Ð EHВ= Ð AFC.
ÐFHD=180°-Ð EHВ =180°-Ð AFC =ÐHFD, отсюда D FHD – равнобедренный, и FD=DH. Находим, что AD=AF+FD=BH+HD=BD.

Список литературы.
1. Арифметические игры для детей 6-7 лет. – М.-Харьков: Илекса, Гимназия, 1998.
2. Афонькин С.Ю. Учимся мыслить логически: Увлекательные задачи для развития логического мышления. – СПб.: Литера, 2002.
3. Беженова М.А. Весёлая математика. – Донецк: Сталкер, 1998.
4. Вайблум Р. Занимательный мир математики. – СПб.: Дельта, 1998.
5. Гарднер М. Математические головоломки и развлечения. – М.: Мир, 1999.
6. Дьячкова О.А. Игры школьников. – М.: Учпедгиз, 1955.
7. Игнатьев Е.И. В царстве смекалки. – М.: Наука, 1978.
8. Игры и развлечения. – СПб.: Валери СПб, 1998.
9. Игры, ребусы, загадки для дошкольников /Сост. Т.И.Линго. – Ярославль: Академия развития, 2001.
Кордемский Б.А. Увлечь школьников математикой. - М.: Просвещение, 1981.
11. Кострикина Н.П. Задачи повышенной трудности в курсе математики 4-5 классов: Книга для учителя. – М.: Просвещение, 1986.
12. Леман И. Увлекательная математика. – М.: Знание, 1985.






