В этом параграфе приведён разбор решений задач типового варианта контрольной работы по математическому анализу.
ЗАДАЧА 1. Вычислить пределы функций а) - е):
А) 

Анализ задачи. Так как для данных дробей степень числителя больше степени знаменателя, то
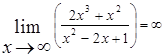 и
и  . Поэтому мы имеем дело с неопределённостью ∞ –∞. Следовательно, теоремой о пределе разности воспользоваться нельзя и необходимо провести тождественные преобразования выражения, находящегося под знаком предела.
. Поэтому мы имеем дело с неопределённостью ∞ –∞. Следовательно, теоремой о пределе разности воспользоваться нельзя и необходимо провести тождественные преобразования выражения, находящегося под знаком предела.
Решение. Приводим выражение к общему знаменателю:
 =
=  =
=  =
=
=  =
=  =
=  / значение дроби не изменится, если ее числитель и знаменатель разделить на одно и то ж е ненулевое число/ =
/ значение дроби не изменится, если ее числитель и знаменатель разделить на одно и то ж е ненулевое число/ = 
Следовательно,  =
=
= 
Ответ: 3
Б) 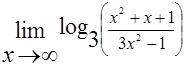
Решение. Вычислим сначала предел логарифмируемого числа:


Из непрерывности функции у(х)=log3x следует, что  если предел lim x-> f(x) существует. Поэтому
если предел lim x-> f(x) существует. Поэтому 
Ответ: -1
Теорема (Первое правило Лопиталя). Пусть функции f(x) и g(x) имеют производные в некоторой окрестности точки а. Если пределы функций равны нулю  и
и 
и если существует предел отношения производных  , то предел отношений функций равен пределу отношения производных
, то предел отношений функций равен пределу отношения производных  =
= 
Теорема (Второе правило Лопиталя). Пусть функции f(x) и g(x) имеют производные в некоторой окрестности точки а. Если пределы функций равны бесконечности  и
и  и если существует предел отношения производных
и если существует предел отношения производных  , то предел отношения функций равен пределу отношения производных
, то предел отношения функций равен пределу отношения производных  =
= 
в) 
Анализ задачи. В данном случае, непосредственное применение теоремы о пределе частного невозможно, поскольку, как показывает подстановка числа -3 вместо х, и предел числителя и предел знаменателя равны нулю.
 и
и 
Таким образом, рассматриваемый предел представляет собой неопределённость вида  и для решения задачи требуется провести тождественные преобразования выражения, находящегося под знаком предела.
и для решения задачи требуется провести тождественные преобразования выражения, находящегося под знаком предела.
Решение. Разложим числитель и знаменатель на множители, пользуясь следующей теоремой: если х1, х2 - корни квадратного трехчлена ах2 + bx + с, то ах2 + bх + с = а (х - хl) (х - х2). Решаем квадратное уравнение, находя его дискриминант D.
3х2 + 8х -= 3 = о; D = b2 - 4ас = 82 + 4 *3 * 3 = 100;
х1,2  ; х2= -3.
; х2= -3.
Отсюда, 3х' + 8х - 3 = 3 (х -  ) (х - (-3)) = (3х -l)(x + 3).
) (х - (-3)) = (3х -l)(x + 3).
Аналогично, х2 + 5х -+- 6 = 0 <=> xl = -2; х2 = -3;
Поэтому х2 + 5х + 6 = (х + 2)(х + 3).
Преобразуем выражение, находящееся под знаком предела:
 / так как функция у=
/ так как функция у=  непрерывна в точке х= -3, подставляем х= -3/=
непрерывна в точке х= -3, подставляем х= -3/=  .
.
Другое решение задачи. Поскольку пределы числителя и знаменателя при х→ -3 равны нулю, применимо правило Лопиталя.

Ответ: 10
г)  .
.
Анализ задачи. Подстановка числа 2 вместо х показывает, что пределы числителя и знаменателя равны нулю. Следовательно, нам потребуется раскрыть неопределенность  . Для этого можно либо провести тождественные преобразования выражения
. Для этого можно либо провести тождественные преобразования выражения  , либо применить правило Лопиталя.
, либо применить правило Лопиталя.
Решение. Выражение  является сопряженным по отношению к выражению
является сопряженным по отношению к выражению  , а выражение
, а выражение  - по отношению к
- по отношению к  . Умножая числитель и знаменатель дроби на произведение сопряжённых выражений
. Умножая числитель и знаменатель дроби на произведение сопряжённых выражений  , и используя формулу разности квадратов
, и используя формулу разности квадратов  , получаем
, получаем 










Другое решение задачи. Воспользуемся правилом Лопиталя 

/ так как функция непрерывна в точке х=2, подставляем х=2 / = 
Ответ: 
Анализ задачи. Подстановка числа 0 вместо х показывает, что предел числителя и предел знаменателя при х→0 равны нулю. Поэтому имеет место неопределённость  . Для того, чтобы раскрыть неопределенность можно либо провести тождественные преобразования выражения
. Для того, чтобы раскрыть неопределенность можно либо провести тождественные преобразования выражения  , либо применить правило Лопиталя.
, либо применить правило Лопиталя.
Решение. Совершим замену неизвестной  ; при этом
; при этом  . Так как у=0 при х=0, то у→0.
. Так как у=0 при х=0, то у→0.



 .
.
Используем теперь тригонометрическую формулу 

= / применяем первый замечательный предел  /
/ 
Другое решение задачи. Воспользуемся вновь правилом Лопиталя
 / подставляем x = 0, cos0 = 1 /
/ подставляем x = 0, cos0 = 1 /  Ответ:
Ответ: 
е) 
Решение: 
= / замена переменной  так как
так как  / =
/ =
 /
/
= / предел произведения равен произведению пределов /  /
/
= / используем второй замечательный предел  /
/ 
Предел  вычислен подстановкой
вычислен подстановкой 
Предел  не может быть вычислен подстановкой
не может быть вычислен подстановкой  , поскольку в результате подстановки получается неопределенность
, поскольку в результате подстановки получается неопределенность  . Ответ:
. Ответ:  .
.
ЗАДАЧА 2. Вычислить производные функции а) – г):
а) Вычислить производную функции  .
.
Решение. Найдем сначала производную функции  :
:
 . Теперь находим в таблице производных сложных функций формулу
. Теперь находим в таблице производных сложных функций формулу  и, подставляя
и, подставляя  , получаем
, получаем  Ответ:
Ответ:  .
.
б) Вычислить производную функции  .
.
Решение. Найдем сначала производную функции  .
.
Так как  , где
, где  , то по таблице производных сложных функций (таблица 2 пункт 2.) находим:
, то по таблице производных сложных функций (таблица 2 пункт 2.) находим:
 .
.
Теперь вычисляем производную функцию у(х), пользуясь формулой производной отношения:

Ответ: 
в) Вычислить производную  .
.
Анализ задачи. Функция  представляет собой произведение трех функций
представляет собой произведение трех функций  . Используя правило Лейбница, можно вывести общую формулу:
. Используя правило Лейбница, можно вывести общую формулу:

Следовательно,

Решение.
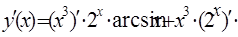
 .
.
Ответ: 

г) Вычислить производную функцию 
Решение. Пользуясь основным логарифмическим тождеством  , представим у(х) в виде
, представим у(х) в виде  . Так как
. Так как 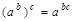 , то
, то  и поэтому
и поэтому  . В последнем равенстве мы вновь воспользовались формулой
. В последнем равенстве мы вновь воспользовались формулой  , читая ее слева на право.
, читая ее слева на право.
Ответ:  .
.
ЗАДАЧА 3. Исследовать функции и построить их графики:
а) исследовать функцию 
Решение.
1) Так как  - многочлен, то функция у(х) определена и непрерывна на всей числовой прямой. Таким образом, область определения данной функции вся – числовая прямая:
- многочлен, то функция у(х) определена и непрерывна на всей числовой прямой. Таким образом, область определения данной функции вся – числовая прямая: 
2) Функция не является ни четной ни нечетной, поскольку  ;
;  ;
;  ;
;  .
.
3) Заметим, что при  и при
и при  поведение многочлена у(х) определяется поведением его старшего члена
поведение многочлена у(х) определяется поведением его старшего члена 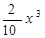 , который неограниченно возрастает при
, который неограниченно возрастает при  и неограниченно убывает при
и неограниченно убывает при  . Поэтому
. Поэтому  .
.
Так как функция у(х) определена на всей числовой оси и  , график функции не имеет асимптот.
, график функции не имеет асимптот.
4) 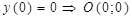 – точка пересечения графика с осью Оу.
– точка пересечения графика с осью Оу.
Для определения точек пересечения графика с осью Ох решим уравнение 



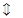
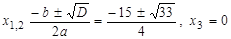 .
.
(в вариантах 5-7 контрольной работы корни уравнения у(х) =0 находятся подбором. Если Вам достался один из этих вариантов, попробуйте подставить числа  .
.
5) Находим локальные экстремумы, а также промежутки возрастания и убывания функции. Для этого вычисляем производную функции 
 ,
, 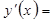
 , и решаем уравнение
, и решаем уравнение 
 , критические точки
, критические точки  . Так как производная не имеет точек разрыва, других критических точек нет. Определяем знак производной справа и слева от каждой критической точки и составляем таблицу:
. Так как производная не имеет точек разрыва, других критических точек нет. Определяем знак производной справа и слева от каждой критической точки и составляем таблицу:

 ;
; 
 ;
; 
 ;
;

| 
| - 4 | 
| -1 | 
|

| + | - | + | ||

| k | максимум | m | минимум | k |
Итак, функция возрастает при  и при
и при  и убывает при
и убывает при  ; локальный минимум –
; локальный минимум –  , локальный максимум –
, локальный максимум – 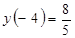 .
.
6) используя пункт 3) получаем, что множество значений функции  – вся числовая прямая,
– вся числовая прямая,  .
.
7) Находим точки перегиба функции и устанавливаем промежутки, на которых график функции обращен выпуклостью вверх и вниз. Для этого, прежде всего, вычисляем производную второго порядка и приравниваем ее к нулю:


Для определения знаков второй производной подставляем в нее числа из промежутков  и
и 
 ;
; 



| 
|
Рис. 1. Графики функций 3.а) и 3.б)

| 
| 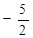
| 
|

| - | + | |

| выпуклость вверх | перегиб | выпуклость вниз |
Теперь необходимо найти значение функции в точке перегиба и определить угол наклона касательной к графику функции в этой точке: 
 , тангенс угла наклона 3 (угол наклона α равен
, тангенс угла наклона 3 (угол наклона α равен  ) равен значению производной в данной точке
) равен значению производной в данной точке  . При построении касательной откладываем 2,0 см от точки А (-2,5; 0,25) по оси Ох вправо и 2,7 см вдоль оси Оу вниз и получаем точку В (-2,5+2; 0,25-2,7), В(-0,5;-2,45). Проводим через точки А и В прямую (АВ). График функции у(х) должен касаться прямой (АВ) в точке А.
. При построении касательной откладываем 2,0 см от точки А (-2,5; 0,25) по оси Ох вправо и 2,7 см вдоль оси Оу вниз и получаем точку В (-2,5+2; 0,25-2,7), В(-0,5;-2,45). Проводим через точки А и В прямую (АВ). График функции у(х) должен касаться прямой (АВ) в точке А.
8) На этом исследование функции закончено и остается лишь вычислить ее значения в некотором числе точек, достаточном для построения графика, и построить график.
б) Исследовать функцию  .
.
Решение.
1). Так как  и
и  , то функция у(х) определена и непрерывна на всей числовой прямой.
, то функция у(х) определена и непрерывна на всей числовой прямой.
2) Функция не является ни четной ни нечетной, поскольку  ;
; 
3) 

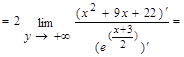




 / замена у = -х /
/ замена у = -х /
 .
.
4) Так как  , то
, то  – точка пересечения графика с осью Оу.
– точка пересечения графика с осью Оу.
Для определения точек пересечения графика с осью Ох решим уравнение у (х) = 0, т.е.  . Так как любая степень числа е положительная, мы можем разделить на
. Так как любая степень числа е положительная, мы можем разделить на  обе части уравнения:
обе части уравнения:  ; D=81-4*22=-7<0.
; D=81-4*22=-7<0.
Поскольку дискриминант отрицателен, уравнение не имеет корней. Иначе говоря, график функции не пересекает ось Ох и поэтому, в силу своей непрерывности, функция у(х) не меняет своего знака на протяжении всей числовой оси. Отсюда вытекает, что у(х)>0 для всех действительных
чисел х, поскольку у(0)>0.
5) Экстремумы. Промежутки возрастания и убывания.


Для определения критических точек функции решим уравнение

критические точки – 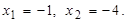


| 
| - 4 | 
| -1 | 
|

| + | - | + | ||

| m | минимум | k | максимум | m |
Локальный минимум –  локальный максимум –
локальный максимум – 
6) Используя пункты 3) -5), получаем, что 
7) Находим точки перегиба и промежутки выпуклости.





| 
| -3 | 
| 
| |

| + | - | + | ||

| вып. вниз | перегиб | вып. вверх | перегиб | вып. вниз |
Теперь необходимо найти значение функции и значение производной (тангенс угла наклона касательной к графику функции) в точках перегиба: 
 , и построить касательные графику функции в этих точках.
, и построить касательные графику функции в этих точках.
8) Так как функция  определена на всей числовой оси и
определена на всей числовой оси и  функция имеет правую горизонтальную асимптоту
функция имеет правую горизонтальную асимптоту 
9) Строим график функции.
ЗАДАЧА 4. Вычислить неопределенные интегралы а) –г):
а)  .
.
Решение. Решение данной задачи требует знания формулы дифференциала функции  . Используя тригонометрическую формулу
. Используя тригонометрическую формулу  , получаем:
, получаем: 
Пусть  . Тогда
. Тогда  , и следовательно,
, и следовательно, 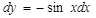 по формуле дифференциала. Отсюда
по формуле дифференциала. Отсюда  .
.


Последнее равенство получено формулам таблицы интегралов:
(1) 
Ответ: 
б) 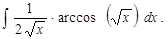
Решение. Решение данной задачи основано на формуле интегрирования по частям:

В этой формуле принимаем за  функцию
функцию  Тогда
Тогда  (так как мы находим первообразную, то «+ С» не пишем).
(так как мы находим первообразную, то «+ С» не пишем).
По формуле  находим производную второго сомножителя
находим производную второго сомножителя 

Подставляя найденные  в формулу интегрирования по частям, получаем:
в формулу интегрирования по частям, получаем:



Ответ: 
в) 
Решение. Так как корнями знаменателя является 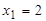 и
и  , то по формуле
, то по формуле 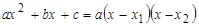 , знаменатели раскладываются на множители.
, знаменатели раскладываются на множители. 
Представим дробь в виде следующей суммы:
 и найдем коэффициенты А и В. Приведем дроби в правой части равенства к общему знаменателю:
и найдем коэффициенты А и В. Приведем дроби в правой части равенства к общему знаменателю:


Приравняв числители, получим
(2)  .
.
Подставляя в последнее равенство  находим, что
находим, что  .
.
Поставляя  в равенство (2), находим, что
в равенство (2), находим, что  .
.
Таким образом,  .
.
Итак,  .
.
Здесь мы воспользовались формулой (1).
Ответ:  .
.
г)  .
.
Анализ задачи. Напомним, что в том случае, когда дискриминант квадратного двучлена  отрицателен,
отрицателен,  , справедливо равенство:
, справедливо равенство:
 .
.
Решение. Для вычисления интеграла  найдем дискриминант знаменателя
найдем дискриминант знаменателя  и рассмотрим функцию
и рассмотрим функцию  . Для последующей замены переменной вычислим производную знаменателя
. Для последующей замены переменной вычислим производную знаменателя  и заметим, что
и заметим, что  ;
;  . Отсюда,
. Отсюда, 

Вычислим получившиеся интегралы по–отдельности.
1)  .
.
2) 
 .
.
Подставляя полученные выражения, окончательно получаем следующий ответ:
 .
.
ЗАДАЧА 5. Вычислить площадь фигуры, ограниченной графиками функций  и
и  . Изобразите эту фигуру на координатной оси.
. Изобразите эту фигуру на координатной оси.
Решение. Графиком функции  является парабола, ветви которой направлены вверх. Вычисляем производную функции
является парабола, ветви которой направлены вверх. Вычисляем производную функции  и находим координаты вершины параболы С.
и находим координаты вершины параболы С.
 ;
;  ;
;  .
.
у = х2 + 3х + 1 | у | 
| у = х + 4 | ||||||||||
| В | |||||||||||||
| А | |||||||||||||

| |||||||||||||
| -3 | С | х |
Рис. к задаче 5
Найдем точки пересечения графиков функций: 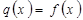 .
.
 ,
,
Заметим, что  графиком функции
графиком функции  является прямая, которую можно построить по двум точкам А (-3;1) и В (1;5).
является прямая, которую можно построить по двум точкам А (-3;1) и В (1;5).
Пусть S – площадь фигуры АВС, ограниченной графиками функций. Так как  при
при 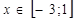 , то
, то 
Ответ:  .
.
УПРАЖНЕНИЯ
1. Предел последовательности
1. Дана постоянная последовательность 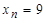 для всех натуральных чисел
для всех натуральных чисел 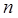 . Докажите, используя определение предела последовательности, что
. Докажите, используя определение предела последовательности, что 
2. Докажите, что 
3. Докажите, используя определение предела последовательности, что 
4. Докажите, используя определение предела последовательности, что  при 0 < q < 1.
при 0 < q < 1.
5. Докажите, что всякая числовая последовательность может иметь не более одного предела.
6. Докажите, что  .
.
7. Докажите, что 
8. Докажите, что 
9. Является ли последовательность  бесконечно малой?
бесконечно малой?
10. Является ли последовательность 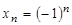 бесконечно малой?
бесконечно малой?
11. Является ли последовательность  бесконечно малой?
бесконечно малой?
12. Найти предел  .
.
13. Найти предел последовательности  .
.
14. Найти предел последовательности  .
.
15. Найти предел последовательности  .
.
16. Найти предел последовательности  .
.
Объясните, какие свойства пределов и теоремы Вы использовали для вычисления этого предела.
17. Найти предел последовательности  .
.
18. Найти предел последовательности  .
.
19. Вычислить предел  .
.
20. Найти предел последовательности 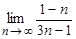 .
.
2. Предел функции. Непрерывность
21. Докажите, что  .
.
22. Найдите, используя определение предела функции, предел функции  при
при  . Используя графические соображения, найдите односторонние пределы
. Используя графические соображения, найдите односторонние пределы  и
и  .
.
23. Докажите, что  .
.
24. Докажите, что  .
.
25. Докажите, что  .
.
26. Докажите, что  .
.
27. Найти предел функции. Докажите, что  .
.
28. Вычислить предел функции  , где
, где  - постоянная величина.
- постоянная величина.
29. Вычислить предел  .
.
30. Вычислить предел  .
.
31. Вычислить предел  .
.
32. Найти предел функции  .
.
33. Найти предел функции  .
.
34. Построить график функции  . Является ли функция
. Является ли функция  непрерывной в точке
непрерывной в точке  ?
?
35. Построить график функции  . Является ли эта функция непрерывной?
. Является ли эта функция непрерывной?
3. Производная
36. Найти производную функции  .
.
37. Найти производную функции  .
.
38. Найти производную функции  .
.
39. Найти производную функции  .
.
40. Найти производную функции  .
.
41. Найти производную функции  .
.
42. Найти производную функции  .
.
43. Найти производную функции  .
.
44. Найти производную функции  .
.
45. Вычислить производную функции 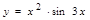 .
.
46. Вычислить производную функции  .
.
47. Вычислить производную функции 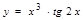 .
.
48. Вычислить производную функции  .
.
49. Вычислить производную функции  .
.
50. Вычислить производную данной функции  .
.
51. Вычислить производную функции:  .
.
52. Пользуясь определением производной как предела отношения приращения функции к приращению аргумента, найдите производную функции  .
.
53. При каком значении параметра p касательная к графику функции  , проведенная в точке с абсциссой
, проведенная в точке с абсциссой  , параллельна прямой
, параллельна прямой  ?
?
54. Выяснить геометрический смысл теоремы Лагранжа.
55. Выяснить геометрический смысл теоремы Ферма.
56. Найти предел функции, пользуясь правилом Лопиталя,  .
.
57. Используя правило Лопиталя, вычислить предел  .
.
58. Найти предел функции, пользуясь правилом Лопиталя  .
.
59. Найти предел функции, пользуясь правилом Лопиталя  .
.
60. Найти предел функции (можно воспользоваться правилом Лопиталя)  .
.
61. Найти предел функции, пользуясь правилом Лопиталя  .
.
62. Найти дифференциал функции 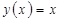 . Найти дифференциал функции
. Найти дифференциал функции  в точке
в точке  .
.
63. Вычислить  .
.
64. Вычислить  .
.
65. Вычислить частные производные функции двух переменных 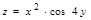 .
.
66. Вычислить частные производные функции двух переменных  .
.
67. Вычислить частные производные функции двух переменных 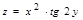 .
.
68. Вычислить частные производные функции двух переменных  .
.
69. Вычислить частные производные функции двух переменных  .
.
70. Вычислить частные производные функции двух переменных  .
.
4. Исследование функций
71. Найти а) точки экстремума функции и б) точки перегиба и направления выпуклости графика функции  .
.
72. Построить график функции  . Найти точки локального экстремума функции
. Найти точки локального экстремума функции  и наибольшее значение этой функции на отрезке
и наибольшее значение этой функции на отрезке  .
.
73. Построить график функции  и найти точку минимума этой функции.
и найти точку минимума этой функции.
74. Исследовать функцию  и построить ее график.
и построить ее график.
75. Найти а) точки экстремума функции и б) точки перегиба и направления выпуклости графика функции:  .
.
76. Найти а) точки экстремума функции и б) точки перегиба и направления выпуклости графика функции: 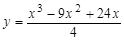 .
.
77. Найти а) точки экстремума функции и б) точки перегиба и направления выпуклости графика функции:  .
.
78. Найти а) точки экстремума функции и б) точки перегиба и направления выпуклости графика функции: 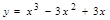 .
.
79. Приведите пример функции, не обладающей на некотором числовом промежутке наибольшим значением.
80. Найти асимптоты функции  .
.
5. Интеграл
81. Вычислить неопределенный интеграл, используя формулу замены переменной  .
.
82. Вычислить неопределенный интеграл, используя формулу замены переменной  .
.
83. Вычислить неопределенный интеграл, используя формулу замены переменной  .
.
84. Используя формулу замены переменной, вычислить неопределенный интеграл  .
.
85. Вычислить неопределенный интеграл, используя формулу интегрирования по частям  .
.
86. Вычислить неопределенный интеграл, используя формулу интегрирования по частям  .
.
87. Вычислить неопределенный интеграл, используя формулу интегрирования по частям  .
.
88. Вычислить неопределенный интеграл, используя метод замены переменной  .
.
89. Вычислить неопределенный интеграл  .
.
90. Вычислить неопределенный интеграл 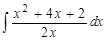 .
.
91. Вычислить определенный интеграл  .
.
92. Вычислить определенный интеграл  .
.
93. Найти  .
.
94. Вычислить определенный интеграл  .
.
95. Вычислить  .
.
96. Вычислить  .
.
97. Вычислить  .
.
98. Вычислить  .
.
99. Найти  .
.
100. Найти  .
.
101. Найти 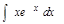 .
.
102. Вычислить  .
.
103. Вычислить неопределенный интеграл  .
.
104. Приведете пример функции, которую нельзя проинтегрировать в элементарных функциях.
105. Вычислить площадь фигуры, ограниченной следующими линиями:  .
.
106. Вычислить площадь фигуры, ограниченной следующими линиями:  .
.
107. Вычислить площадь фигуры, ограниченной следующими линиями:  .
.
108. Вычислить площадь фигуры, ограниченной следующими линиями:  .
.
109. Вычислить площадь фигуры, ограниченной следующими линиями: 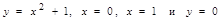 .
.
КОНТРОЛЬНАЯ РАБОТА №1
Формулировки условий задач контрольной работы:
1. Вычислить предел функции.
2. Вычислить производную функции.
3. Исследовать функции  и
и  построить их графики.
построить их графики.
4. Вычислить неопределенные интегралы.
5. Вычислить площадь фигуры, ограниченной графиками функций  и
и  .
.
ВАРИАНТ 0
1.
а) 
| б) 
|
в) 
| г) 
|
д) 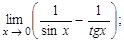
| е) 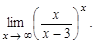
|
2.
а) 
| б) 
|
в) 
| г)  . .
|
3.
а) 
| б)
Дата добавления: 2015-11-05; Мы поможем в написании ваших работ!; просмотров: 550 | Нарушение авторских прав Поиск на сайте: Лучшие изречения: |
Ген: 0.012 с.









