МАТЕМАТИЧЕСКИЕ МЕТОДЫ В МЕНЕДЖМЕНТЕ
Методические указания и контрольные задания
для студентов-заочников экономических специальностей
аграрного университета
Саратов 2015
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Программные вопросы
1. Основная задача линейного программирования. Теорема об оптимальном плане.
2. Графический метод решения задач линейного программирования.
3. Симплекс-метод решения задач линейного программирования в канонической форме.
3. Транспортная задача и её решение методом потенциалов.
Литература:
1. Бось, В.Ю., Иоанно, А.Д., Н.Б. Уейская Экономико-математические методы: учебное пособие / В.Ю. Бось, А.Д. Иоанно, Н.Б. Уейская. ФГОУ ВПО «Саратовский ГАУ». - Саратов. 2009.- 188с.
2. Экономико-математические методы и модели: учебное пособие /Под ред. С.И. Макарова. – М.: КНОРУС, 2009. – 240с.
Пример 1. Требуется решить задачу линейного программирования графическим методом:
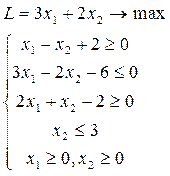
Решение. Построим сначала область допустимых решений, которая представляет собой множество решений системы линейных ограничений.
Графически решение каждого неравенства есть одна из полуплоскостей, на которые прямая линия ax +by =c делит координатную плоскость. Решением системы неравенств будет выпуклый многоугольник, представляющий собой пересечение полуплоскостей – решений каждого неравенства.
Пронумеруем каждое неравенство и решим его (см. рис.1.1)
1. 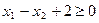
Построим прямую  , для чего найдём координаты двух её точек, например, (0; 2) и (2; 4). Чтобы выбрать полуплоскость-решение для данного неравенства, подставим в это неравенство координаты любой точки, не лежащей на построенной прямой, например точки с координатами (0; 0). Получаем 0 – 0 +2
, для чего найдём координаты двух её точек, например, (0; 2) и (2; 4). Чтобы выбрать полуплоскость-решение для данного неравенства, подставим в это неравенство координаты любой точки, не лежащей на построенной прямой, например точки с координатами (0; 0). Получаем 0 – 0 +2 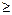 0. Это верное неравенство. Следовательно, полуплоскость, содержащая эту точку, будет являться решением неравенства 1. Стрелками отметим решение.
0. Это верное неравенство. Следовательно, полуплоскость, содержащая эту точку, будет являться решением неравенства 1. Стрелками отметим решение.
2. 
Строим прямую  , проходящую через точки с координатами (0;-3) и (2;0). Решением неравенства является полуплоскость, содержащая начало координат (0,0), так как: 3∙0 –2∙ 0 – 6
, проходящую через точки с координатами (0;-3) и (2;0). Решением неравенства является полуплоскость, содержащая начало координат (0,0), так как: 3∙0 –2∙ 0 – 6  0 - верное неравенство.
0 - верное неравенство.
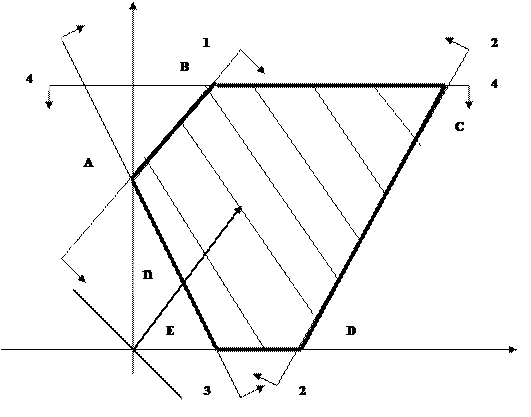
Рис. 1. Решение задачи линейного программирования.
3. 
Строим прямую  , проходящую через точки с координатами (0;2) и (1;0). Затем в неравенство подставляем координаты точки (0;0): 2∙0 + 0 – 2
, проходящую через точки с координатами (0;2) и (1;0). Затем в неравенство подставляем координаты точки (0;0): 2∙0 + 0 – 2 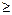 0. Так как это неравенство неверное, то решением является полуплоскость, не содержащая точку с координатами (0;0).
0. Так как это неравенство неверное, то решением является полуплоскость, не содержащая точку с координатами (0;0).
4. 
Прямая, определяемая уравнением 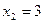 проходит через точку (0;3) параллельно оси абсцисс. Полуплоскость, лежащая ниже этой прямой и есть решение данного неравенства.
проходит через точку (0;3) параллельно оси абсцисс. Полуплоскость, лежащая ниже этой прямой и есть решение данного неравенства.
Два последних неравенства 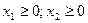 определяют первый квадрант координатной плоскости.
определяют первый квадрант координатной плоскости.
На рис. 1 многоугольник ABCDE представляет собой область допустимых решений задачи линейного программирования.
Для нахождения оптимального решения построим вектор  (3;2), координаты которого равны коэффициентам при переменных в целевой функции L. Этот вектор является нормальным вектором для линий уровня L=const, а также одну из линий уровня, например,
(3;2), координаты которого равны коэффициентам при переменных в целевой функции L. Этот вектор является нормальным вектором для линий уровня L=const, а также одну из линий уровня, например,  . Так, как задача на отыскание максимального значения целевой функции, то линию уровня перемещаем в направлении нормали до опорной прямой, то есть такой линии уровня, которая имеет хотя бы одну общую точку с областью допустимых решений и по отношению к которой эта область находится в одной из полуплоскостей. Эта прямая проходит через точку С пересечения прямых
. Так, как задача на отыскание максимального значения целевой функции, то линию уровня перемещаем в направлении нормали до опорной прямой, то есть такой линии уровня, которая имеет хотя бы одну общую точку с областью допустимых решений и по отношению к которой эта область находится в одной из полуплоскостей. Эта прямая проходит через точку С пересечения прямых  и
и 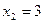 , для определения координат точки С решим систему уравнений
, для определения координат точки С решим систему уравнений  , получаем С(4;3) в этой точке целевая функция достигает максимума
, получаем С(4;3) в этой точке целевая функция достигает максимума  .
.
Ответ:  при Х*= (4;3).
при Х*= (4;3).
Пример 2. Требуется решить задачу линейного программирования симплекс-методом:
L = 4x1 + 2x2 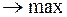

х1 ≥ 0, х2 ≥ 0
Решение. При решении используем
Алгоритм симплекс-метода.
1. Составляем математическую модель задачи.
2. Приводим задачу к канонической форме: путём введения новых переменных преобразуем систему ограничений к системе уравнений, а затем приравниваем целевую функцию её свободному члену. Свободные члены в системе ограничений должны быть неотрицательны.
3. Выделяем базисные переменные в каждом уравнении системы ограничений. Базисная переменная в данном уравнении имеет коэффициент равный единице, а в остальных уравнениях и в целевой функции он равен нулю.
4. Составляем симплексную таблицу: записываем в первом столбце базисные переменные, во втором – свободные члены, а затем коэффициенты при переменных.
5. Получаем опорный план. Все планы получаются одинаково: небазисные переменные равны нулю, а базисные переменные и целевая функция равны свободным членам.
6. Выбираем разрешающий столбец, то есть столбец коэффициентов при переменной, которая на данном шаге вводится в базис. При решении задачи на максимум в строке коэффициентов при переменных целевой функции находим наибольшее по абсолютной величине отрицательное число; при решении задачи на минимум – наибольшее положительное число. Если разрешающий столбец найти нельзя, то полученный план – оптимальный.
7. Находим разрешающую строку. При решении задачи на максимум или на минимум она находится одинаково: выбирается наименьшее из отношений свободных членов к положительным коэффициентам разрешающего столбца. Если разрешающую строку найти нельзя, то задача не имеет решения.
8. Находим разрешающий элемент, стоящий на пересечении разрешающего столбца и разрешающей строки.
9. Составляем новую симплексную таблицу, в которую вносим разрешающую строку, поделённую на разрешающий элемент. Остальные строки находим путём получения нулей в разрешающем столбце с помощью разрешающей строки.
10. Получаем новый план и переходим к пункту 6.
Приведем задачу к канонической форме:

хj ≥ 0 (j=1,2,3,4,5,6)
Целевую функцию приравняем свободному члену:
L – 4х1 – 2х2 = 0 → max
Выберем базисные переменные Б = (х3, х4, х5, х6) и составим первую симплексную таблицу.
| Базисные переменные | Свободные Члены | х1 | х2 | х3 | х4 | х5 | х6 |
| х3 | |||||||
| х4 | |||||||
| х5 | |||||||
| х6 | |||||||
| L | -4 | -2 |
Первоначальный, или опорный план данной задачи будет следующий:
Х0 = (0, 0, 5, 14, 10, 8), а значение целевой функции L0 = 0.
Выбираем разрешающий столбец и разрешающую строку. Так как задача на отыскание максимального значения L, то ищем в последней строке таблицы наибольшее по абсолютной величине отрицательное число, это (-4), следовательно, столбец соответствующий х1 будет разрешающим. Выделим его в таблице.
Для отыскания разрешающей строки найдем 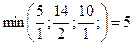 , это соответствует первой строке, следовательно, она будет разрешающей. Выделим ее в таблице. Итак, будем вводить в число базисных переменных х1 вместо х3. Получаем Б = (х1, х4, х5, х6)
, это соответствует первой строке, следовательно, она будет разрешающей. Выделим ее в таблице. Итак, будем вводить в число базисных переменных х1 вместо х3. Получаем Б = (х1, х4, х5, х6)
Разрешающий элемент равен 1, поэтому в новую симплексную таблицу перепишем разрешающую строку без изменения. Ко второй строке прибавим разрешающую, умноженную на (-2). К третьей строке прибавим разрешающую, умноженную на (-1). В четвертой строке разрешающего столбца стоит 0, поэтому перепишем ее без изменения. К последней строке прибавим разрешающую, умноженную на 4. Получили вторую симплексную таблицу и новый план:
| Базисные переменные | Свободные члены | х1 | х2 | х3 | х4 | х5 | Х6 |
| х1 | |||||||
| х4 | -2 | ||||||
| х5 | -1 | ||||||
| х6 | |||||||
| L | -2 |
Х1 = (5, 0, 0, 4, 5, 8), при этом L1 = 20. Этот план лучше предыдущего. Можно ли его улучшить?
В строке для целевой функции есть отрицательное число (- 2), оно соответствует разрешающему столбцу. Для нахождения разрешающей строки найдем 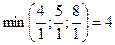 , это соответствует второй строке, она и будет разрешающей. Следовательно будем вводить в базис х2 вместо переменной х4. Получаем Б = (х1, х2, х5, х6) и строим следующую симплексную таблицу. Разрешающий элемент равен 1, поэтому в новую таблицу разрешающую строку переносим без изменения. Нули в разрешающем столбце получаем следующим образом: к третьей и четвертой строкам прибавляем разрешающую, умноженную на (-1), а к последней прибавляем разрешающую строку, умноженную на 2. В первой строке разрешающего столбца стоит 0, поэтому переписываем ее без изменения. Получаем третью симплексную таблицу:
, это соответствует второй строке, она и будет разрешающей. Следовательно будем вводить в базис х2 вместо переменной х4. Получаем Б = (х1, х2, х5, х6) и строим следующую симплексную таблицу. Разрешающий элемент равен 1, поэтому в новую таблицу разрешающую строку переносим без изменения. Нули в разрешающем столбце получаем следующим образом: к третьей и четвертой строкам прибавляем разрешающую, умноженную на (-1), а к последней прибавляем разрешающую строку, умноженную на 2. В первой строке разрешающего столбца стоит 0, поэтому переписываем ее без изменения. Получаем третью симплексную таблицу:
| Базисные переменные | Свободные члены | х1 | х2 | х3 | х4 | х5 | х6 |
| х1 | |||||||
| х2 | -2 | ||||||
| х5 | -1 | ||||||
| х6 | -1 | ||||||
| L |
Получили новый план Х2 = (5, 4, 0, 0, 1, 4), при этом L2 = 28. Этот план лучше предыдущего. Очевидно, что найденный план оптимальный, так как в последней строке больше нет отрицательных чисел, и, следовательно, увеличить значение целевой функции невозможно. Максимум целевой функции Lmax = 28 достигается при плане Х2 = (5, 4, 0, 0, 1, 4).
Ответ: Х* = (5, 4, 0, 0, 1, 4), Lmax = 28.
Пример 3. Требуется составить оптимальный план доставки 135 ед. груза oт трех поставщиков, у которых имеется соответственно 55, 65 и 15 ед. груза к трем потребителям. Причем первому из них требуется 35 ед. груза, второму - 60 ед. и третьему - 40 ед. Стоимости перевозки 1 ед. груза (тарифы) приведены в таблице:
| Поставщики | Потребители | ||
| В1 | В2 | В3 | |
| А1 | |||
| А2 | |||
| А3 |
Решение. Алгоритм метода потенциалов предусматривает следующие этапы решения транспортных задач:
1). Условия задачи записываются в транспортную таблицу:
 Bj
Ai Bj
Ai
| B1 | B2 | B3 | a i |
| A1 |  1 1
|  3 3
|  6 6
| |
| A2 |  4 4
|  2 2
|  3 3
| |
| A3 |  2 2
|  1 1
|  5 5
| |
| bj |
Ресурсы поставщиков записывают в столбце аi, потребности потребителей – в строке bj, тарифы – в левом верхнем углу соответствующих клеток таблицы;
2). Составляется опорный план. Наиболее эффективным методом для его получения является метод наилучших оценок. Самые низкие тарифы, равные 1, в клетках (1,1) и (3,2), то есть наиболее выгодные (самыми дешевыми) являются поставки груза от поставщика А1 к потребителю В1 и от А3 к В2. С этих клеток начинается планирование грузоперевозок. Итак, потребителю В1 необходимо 35 ед. груза. Поставщик А1, наиболее эффективный для этого потребителя, может удовлетворить его потребности полностью. Поэтому в клетку (1,1) записывается величина поставки 35. Для потребителя В2 наиболее эффективный поставщик А3 может обеспечить лишь часть его потребности в грузе. Поэтому в клетку (3,2) записывается величина поставки 15, составляющая весь ресурс А3. Недостающие 45 ед. груза обеспечивает поставщик А2, являющийся наиболее эффективным после А3 поставщиком груза для В2. Наконец, для потребителя В3 наиболее эффективным является поставщик А2, оставшийся ресурс которого позволяет обеспечить 20 ед. груза для В3. Недостающие 20 ед. груза можно взять только у А1.
В результате получается опорный план  . Суммарные транспортные расходы (величина целевой функции задачи) в данном случае будут равны
. Суммарные транспортные расходы (величина целевой функции задачи) в данном случае будут равны
C0 = 1∙35 + 6∙20 + 2∙45 + 3∙20 + 1∙15 = 320;
3). Полученный план проверяется на невырожденность. Невырожденным считается вариант плана, в котором количество заполненных клеток l =
= m + n – 1, где т – число поставщиков, а п – число потребителей. Для представленного в транспортной таблице варианта плана имеем:
m = 3, n = 3, l = 5 = m + n – 1. Следовательно, данный вариант плана является невырожденным.
Необходимо заметить, что в случае l< m + n – 1 невырожденности плана добиваются, заполнением недостающих клеток нулями, причём целесообразно выбирать клетки с меньшими тарифами.
4). План проверяется на оптимальность. С этой целью вводят потенциалы строк Ui и потенциалы столбцов Vj. Индексы i или j потенциалов означают номера соответствующих поставщиков или потребителей.
Для всех заполненных клеток должно выполняться условие
Ui + Vj = Сij.
Для рассматриваемого плана получаем систему уравнений:

Эта система линейных уравнений неопределенна, поскольку для нахождения 6 потенциалов имеется только 5 уравнений. Чтобы получить какое-либо её решение, один из потенциалов полагают равным произвольному числу. Пусть для определенности U1 = 0. Тогда остальные 6 неизвестных потенциалов однозначно определяются из системы уравнений:
U2 = - 3, U3 = - 4, V1 = 1, V2 = 5, V3 = 6.
Полученные значения потенциалов записывает в соответствующие клетки транспортной таблицы:
| Bj Ai | B1 | B2 | B3 | ai | Ui |
| A1 |  1 1
|  3 3
|  6 6
| ||
| A2 |  4 4
|  2 2
|  3 3
| -3 | |
| A3 |  2 2
|  1 1
|  5 5
| -4 | |
| bj | |||||
| Vj |
Далее, для каждой незаполненной клетки определяют ее оценки по формуле:
∆(i, j) = Cij – (Ui + Vj) (2.3.2)
Для рассматриваемого плана получаются следующие оценки незаполненных клеток:
∆( 1,2 ) = 3 - (0 + 5) = -2,
∆( 2,1 ) = 4 - (-3 + I) = 6,
∆( 3,1 ) = 2 - (-4 + I) = 5.
∆( 3,3 ) = 5 - (-4 + 6) = 3.
При оптимальном плане для всех незаполненных клеток их оценки неотрицательные.
В нашем случае полученный план перевозки грузов Хо не является оптимальным и может быть улучшен путем перераспределения части груза в клетку (1,2), имеющую отрицательную оценку, где нарушается условие оптимальности.
Примечание: если при проверке плана на оптимальность оказывается, что несколько незаполненных клеток имеют отрицательные оценки, то груз перераспределяют в клетку с наиболее отрицательной оценкой. Если же наиболее отрицательная оценка получается у двух или более клеток, то груз перераспределяют в клетку с наименьшим среди них тарифом;
5). Составляется новый вариант плана. С этой целью для клетки (1,2), в которой не выполняется признак оптимальности, строится «замкнутый маршрут», который представляет собой замкнутый многоугольник с прямыми углами, все вершины которого расположены в заполненных клетках, кроме одной – (1,2).
|
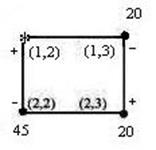
ется наименьшая величина поставки (в данном случае min { 20;45 } = 20) и она прибавляется к запланированному объему грузоперевозки в клетках, где вершины обозначены знаком (+), и вычитается из запланированного объема грузоперевозки в клетках, где вершины обозначены знаком (-). В результате получается вариант плана  .
.
Суммарные транспортные расходы (величина целевой функции) при таком плане составляют
C1 = 1∙35 + 3∙20 + 2∙25 + 1∙15 + 3∙40 = 280.
При этом С1 <C0.
Результаты запишем в новую транспортную таблицу:
 Bj
Ai Bj
Ai
| B1 | B2 | B3 | ai | Ui |
| A1 |  1 1
|  3 3
|  6 6
| ||
| A2 |  4 4
|  2 2
|  3 3
| ||
| A3 |  2 2
|  1 1
|  5 5
| ||
| bj | |||||
| Vj | V1 = -2 | V2 = 0 | V3 = 1 |
Далее алгоритм метода потенциалов повторяется. Полученный план проверяется сначала на невырожденность, а затем – на оптимальность. В этом случае имеем:

Отсюда, полагая V2 = 0, получаем: U1 = 3, U2 = 2, U3 = 1, V1 = -2, V3 = 1.
Оценки незаполненных клеток согласно (3,2) будут таковы:
∆( 1,3 ) = 6 - (3 + 1) = 2,
∆( 2,1 ) = 4 - (2 - 2) = 4,
∆( 3,1 ) = 2 - (1 - 2) = 3,
∆( 3,3 ) = 5 - (1 + 1) = 3.
Поскольку все оценки неотрицательные, заключаем, что найденный нами план является оптимальным.
Ответ:  ; Сmin = 280.
; Сmin = 280.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Заочная форма обучения предполагает самостоятельную работу студента над учебным материалом: изучение учебной литературы, выполнение контрольных заданий. В случае возникновения затруднений студент может обратиться за консультацией к преподавателю кафедры высшей математики.
В соответствии с действующим учебным планом студент должен выполнить одну контрольную работу и сдать зачет.
При выполнении контрольной работы студент обязан руководствоваться следующими требованиями:
1. Контрольная работа выполняется в отдельной тетради в клетку, на титульном листе которой должны быть ясно написаны фамилия студента, его инициалы, полный шифр, дата её отсылки, домашний адрес студента.
2. Перед решением каждой задачи необходимо полностью переписать её условие.
3. Решение задачи следует записывать аккуратно в соответствии с порядком решения.
4. Контрольная работа должна быть выполнена самостоятельно.
5. В случае незачёта по контрольной работе студент обязан в кратчайший срок исправить все отмеченные рецензентом ошибки и недочёты и предъявить работу на повторное рецензирование, приложив при этом первоначально выполненную работу.
6. Номер варианта контрольной работы должен совпадать с последними цифрами учебного шифра студента.






