В реальных условиях колеблющаяся материальная точка всегда испытывает сопротивление движению. Рассмотрим прямолинейное движение материальной точки под действием восстанавливающей силы и силы вязкого сопротивления.
Дифференциальное уравнение колебаний при действии восстанавливающей силы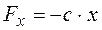 
и силы 
сопротивления имеет следующий вид:
;
Введем коэффициент
получим дифференциальные уравнения свободных колебаний при наличии вязкого сопротивлении
,
Коэффициент k – круговая частота – характеризует восстанавливающую силу, а коэффициент h характеризует силу сопротивления. Эти коэффициенты сопоставимы и имеют размерность 1/с.
Колебательный процесс существенно зависит от соотношения величин h и k.
Рассмотрим несколько случаев.
1. Случай малого сопротивления (h < k). Общее решение дифференциального уравнения:
,
где 
.
Колебания, происходящие по данному закону, называют затухающими, так как амплитуда 
с течением времени непрерывно уменьшается.
График, характеризующий данные колебания представлен на рис.3.12.
Рис.3.12
Влияние силы сопротивления выражается в том, что амплитуда колебаний уменьшается в геометрической прогрессии со знаменателем
,
где период затухающих колебаний
во все время движения остается постоянным. Величина η называется декрементом колебаний (фактором затуханий). Рассматривают также логарифмический декремент колебаний: 
.
В случае малых сопротивлений влиянием сопротивлений на величину периода колебаний можно пренебречь, полагая что
2. При случае, когда 
(граничный случай)
Уравнения движения точки примут следующий вид
Из этой зависимости следует, что в рассматриваемом случае движение точки уже не носит колебательного характера, но остается затухающим движением, так как при 
.
Такое движение называется апериодическим. В данном случае точка, получив начальную скорость, достигнет положения, соответствующего максимальному отклонению от положения равновесия. А далее будет приближаться к положению равновесия. Ниже показан график, отражающий данный случай.
Вынужденные колебания
Пусть на материальную точку действуют восстанавливающая сила 
и возмущающая сила 
. При этом величина k будет являться угловой частотой собственных колебаний, а величина p – угловой частотой вынужденных колебаний. Силу сопротивления мы не учитываем.
Дифференциальное уравнение вынужденных колебаний:
;
,
где 
- приведенная амплитуда возмущающей силы.
Уравнение движения в зависимости от соотношения величин k и p имеет различный вид. В случае, когда 
,
,
где 
, 
- постоянные интегрирования.
Амплитуда чисто вынужденных колебаний:
.
С другой стороны, воспользовавшись уравнениями , 
получим:
.
Величина 
называется коэффициентом динамичности. Данный коэффициент показывает, во сколько раз амплитуда колебаний превосходит статическое отклонение 
при действии максимальной возмущающей силы H.
Рассмотрим случай, когда 
. Уравнение движения при этом будет такое же как и в предыдущем случае. График колебаний представлен на рис.3.13.
Рис.3.13
Такое движение называется биением.
Случай, когда 
. Уравнение движения:
.
График колебаний представлен на рис.3.14.
Рис.3.14
При таком движении происходит неограниченный рост амплитуды со временем. Это явление носит название резонанса. При резонансе коэффициент динамичности стремится к ∞.
Решение задач
Условие задачи. Стержень OA длины l, на конце которого помещен груз массы m, может поворачиваться относительно оси O (рис. 3.15). На расстоянии a от оси O к стержню прикреплена пружина с коэффициентом жесткости c. определить круговую частоту колебаний груза, если стержень в положении равновесия занимает горизонтальное положение. Массой стержня пренебречь.
Рис.3.14
Решение. Круговую частоту колебаний груза определим по формуле
. (3)
Для этого сначала найдем эквивалентную жесткость 
эквивалентной пружины.
Рассмотрим равновесие груза A, укрепленного на стержне. Уравнение моментов относительно точки O сил, действующих на груз, будет иметь следующий вид:
,
где 
- сила упругости пружины в положении равновесия груза. Откуда
. (4)
Рассмотри теперь равновесие груза A на эквивалентной пружине. Уравнение равновесия груза имеет следующий вид:
,
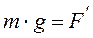где 
- сила упругости эквивалентной пружины в положении равновесия груза. С учетом этого получим
(5)
Приравнивая правые части выражений (4) и (5), получим
. (6)
Отношение 
найдем как отношение сторон a и l соответственно треугольника OAB:
. С учетом этого выражение (6) примет вид
.Найденное значение подставим в формулу (1):
.
ПРИМЕР 2. Найти период свободных вертикальных колебаний корабля на спокойной воде, если масса корабля М т, площадь его горизонтальной проекции S м2. Плотность воды ρ= 1 т/м3. Силами, обусловленными вязкостью воды, пренебречь.
РЕШЕНИЕ. В процессе вертикальных колебаний на корабль действуют две силы: сила тяжести M g и выталкивающая корабль из воды сила Архимеда FA. Условно, изобразим корабль в двух положениях (рис. 3.15); положении статического равновесия 1 и в произвольном положении 2 определяемом координатой x.
Рис. 3.15
Составим дифференциальное уравнение движения центра тяжести корабля:
Получено уравнение вида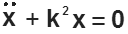 
,
где 
Следовательно,
