ДИНАМИКА
Динамика – раздел теоретической механики, в котором изучается движение тел под действием сил.
Динамика - наиболее общий раздел механики. Так, среди практических задач механики лишь их небольшое число требует чисто статического или кинематического исследования. В большинстве случаев, проводиться полное, динамическое изучение тех или иных явлений. В этом плане статику и кинематику можно рассматривать как введение в динамику, хотя они имеют и самостоятельное прикладное значение.
В основу динамики положены исходные положения (аксиомы) впервые высказанные Ньютоном и Галилеем в 17 веке.
Основные законы динамики сформулированы применительно к материальной точке.
В основе классической механики лежат два допущения. Последними утверждается существование абсолютного пространства и абсолютного времени. Полагается, что пространство обладает чисто геометрическими свойствами, а время не зависит от движения системы отсчета.
В динамике принимается также, что массы движущихся материальных объектов не зависят от скорости их движения.
Масса – мера инертных и гравитационных свойств тела. Измеряется в системе СИ в килограммах. [m] = [кг].
Основные законы динамики.
Закон инерции:
(первый закон Ньютона) если действующая на материальную точку система сил уравновешена или эквивалентна нулю, то точка находится либо в покое, либо в состоянии прямолинейного движения.
Изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения.
Под изолированной, понимается материальная точка, не взаимодействующая с другими телами, или когда силы действующие на точку, взаимно уравновешиваются.
Система отсчета в которой выполняется первый закон Ньютона, т.е. система в которой изолированная материальная точка движется равномерно и прямолинейно или находится в состоянии покоя называется инерциальной системой отсчета. Инерциальная система отсчета – система отсчета, которую можно считать неподвижной.
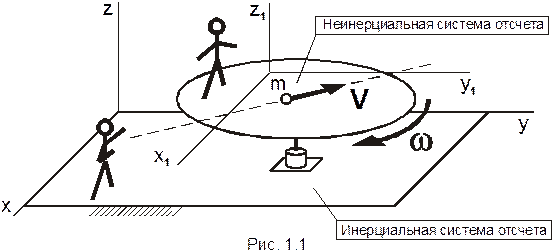
Система отсчета не обладающая этими свойствами, называются неинерциальной системой отсчета. В последней, точка на которую не действуют силы, движется с ускорением и её скорость может меняться как по величине, так и по направлению (рис. 1.1). Неинерциальная система отсчета – движущаяся система отсчета. При решении задач чаще всего за инерциальную систему отсчета принимают геоцентрическую (связанную с землей) систему отсчета. При расчете объектов больших масс и с большими скоростями за инерциальную систему отсчета можно принять гелиоцентрическую (связанную с солнцем) систему отсчета.
Основной закон динамики:
этим законом является второй закон Ньютона.
В аналитической форме этот закон представляет основное уравнение динамики
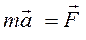
где F - сила, a - ускорение, m - масса, являющаяся мерой инертных свойств материальной точки.
Ускорение тела пропорционально силе вызывающей это ускорение.
Или: сила действующая на материальную точку, сообщает ей ускорение, которое в инерциальной системе отсчета пропорционально величине и имеет направление силы.
Единица массы в системе СИ - 1 кг. Один килограмм равен массе 1 дм3 чистой воды при температуре 40 С. Единица силы - 1 Ньютон (1Н). Один Ньютон - сила сообщающая массе 1 кг ускорение 1 м/с2.
Третий закон Ньютона (Закон равенства действия и противодействия)
Две материальные точки взаимодействуют друг с другом с силами равными по величине и направленными в противоположные стороны.
Закон независимости действия сил. (Закон суперпозиции).
При действии на материальную точку нескольких сил её ускорение равно сумме ускорений, которые имела бы точка при действии на неё каждой силы в отдельности.
Это значит, что при действии на материальную точку сил 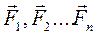 каждая из которых сообщает точке ускорения
каждая из которых сообщает точке ускорения 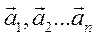 ускорение
ускорение
. 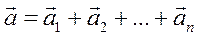
На основании второго закона Ньютона
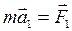
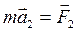
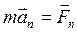
Складывая эти равенства, получим
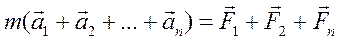
или, на основании закона независимости сил
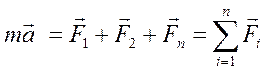
где Fi - равнодействующая всех сил, приложенных к материальной точке.
Таким образом, движение материальной точки под действием сил F1, F2, …, Fn, будет таким же, как и при действии одной силы, равной их геометрической сумме (равнодействующей).
Выражение 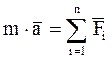 называют основным уравнением динамики материальной точки.
называют основным уравнением динамики материальной точки.
ДИНАМИКА ТОЧКИ
3.2.1. Дифференциальные уравнения движения материальной точки
Пусть r - радиус вектор (рис. 1.2) определяющий положение точки в инерциальной системе отсчета.
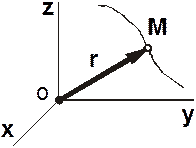
Рис.3.2.
Тогда ускорение точки
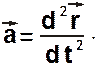
С учетом этого, основное уравнение динамики 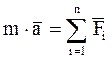 можно записать в виде:
можно записать в виде:
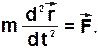
Полученное выражение является также дифференциальным уравнением движения материальной точки в векторной форме.
Проектируя обе части последнего векторного равенства на оси прямоугольной системы координат получим скалярные выражения представляющие собой дифференциальные уравнения движения точки в осях x, y, z:
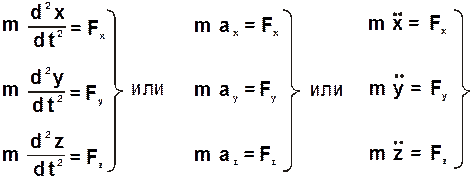
Дифференциальные уравнения движения точки при естественном способе задания движения получаются в результате проектирования основного уравнения динамики на оси естественного тетраэдра (рис. 1.3):
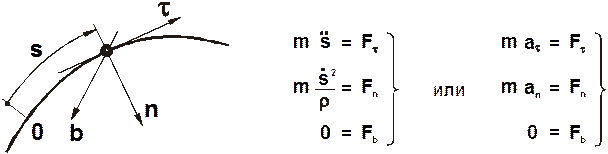
Рис.3.3.
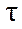 - касательная к траектории, n – нормаль, b – бинормаль,
- касательная к траектории, n – нормаль, b – бинормаль, 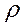 - радиус кривизны траектории.
- радиус кривизны траектории.
3.2.2. ДВЕ ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ
Первая задача. Зная массу точки и закон её движения, определяют действующие на точку силы.
Так, если движение точки задано в прямоугольной системе координат, то суть задачи состоит в следующем:
Дано: m, x = f (t), y = f (t), z = f (t).
----------------------------------------------------------
Определить: Fx, Fy, Fz.
В основе решения первой задачи динамики точки лежит дифференцирование её уравнений движения.
Пример 1.
 Дано:
Дано: 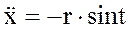
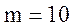 кг
кг 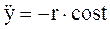
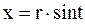
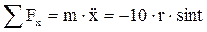

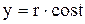
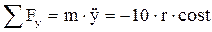

 F -?
F -? 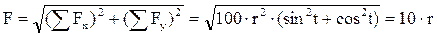
F – равнодействующая системы сил.
Пример 2.
 Дано:
Дано: 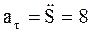 м/с2
м/с2
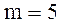 кг
кг 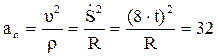 м/с2
м/с2
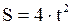 (см.рис.1.4)
(см.рис.1.4)
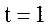 с
с
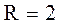 м
м
 |
F -?
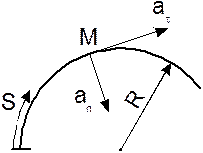
Рис.1.4.
Сила имеет направление ускорения, которое она сообщает.
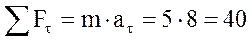 Н
Н
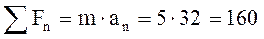 Н
Н
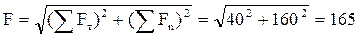 Н
Н
Вторая основная задача динамики
Вторая задача. Зная массу точки и действующие на неё силы, определяют закон её движения.
При задании движения точки в прямоугольной системе координат задача имеет вид:
Дано: m, Fx, Fy, Fz.
----------------------------------------------------
Определить: x = f (t), y = f (t), z = f (t).
В основе решения второй задачи динамики лежит интегрирование дифференциальных уравнений движения.. При этом, следует иметь в виду, что сила действующая на материальную точку может быть постоянной или зависеть от времени, координат движущейся точки и её скорости. Следовательно, в общем случае, вторая задача динамики сводится к необходимости решения системы дифференциальных уравнений, как например:
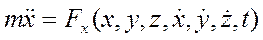
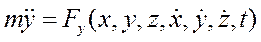
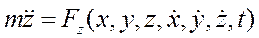
в которые искомые функции x, y и z входят вместе со своими первыми и вторыми производными.
Если точка несвободна, то в правую часть уравнения войдут также неизвестные реакции связи.
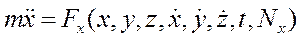
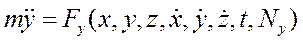
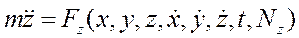
Поэтому вторая задача динамики в этом случае состоит в том, что бы зная действующие на точку активные силы, определить ее движение и реакции наложенных на нее связей.
При решении второй задачи динамики в общем виде решение может быть представлено в виде:
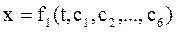
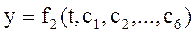
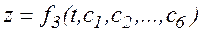
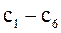 - постоянные интегрирования, которые определяются путем подстановки в уравнения начальных условий.
- постоянные интегрирования, которые определяются путем подстановки в уравнения начальных условий.
Для определения каждого коэффициента c необходимо в правую часть уравнения вместо времени подставить 0 (t0 = 0), а в левую часть уравнения начальные значения рассчитываемого параметра.
Таким образом, окончательное решение второй задачи динамики можно представить в виде:
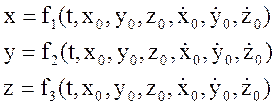
Обратные задачи динамики материальной точки рекомендуется решать в следующем порядке:
1) выбрать систему координат;
2) записать начальные условия движения точки;
3) изобразить на рисунке задаваемые силы и силы реакции связей;
4) составить дифференциальные уравнения движения материальной точки;
5) проинтегрировать систему дифференциальных уравнений движения. Используя начальные условия движения точки, определить постоянные интегрирования;
6) воспользовавшись уравнениями движения материальной точки, определяем искомые величины.
При составлении дифференциальных уравнений движения необходимо рассматривать точку в текущем положении.
Вторая основная задача динамики на практике встречается гораздо чаще.
Задача интегрирования системы дифференциальных уравнений при заданных начальных условиях в общем случае является довольно трудоемкой. Даже в простейшем случае прямолинейного движения, когда имеется одно дифференциальное уравнение, его решение удается выразить точно в квадратурах лишь при определенной зависимости силы от времени, координаты и скорости.
Таким образом, наиболее важные случаи прямолинейного движения материальной точки получаются тогда, когда сила постоянная величина или она зависит только от времени, или от координат, или от скорости. Поэтому вторую задачу динамики в зависимости от действующих сил можно подразделить:
1. Сила – постоянная величина
2. Сила зависит от расстояния
3. Сила зависит от скорости
4. Сила зависит от времени
Если сила постоянная величина, имеем случай равнопеременного движения, т.е. движение с постоянным ускорением. От времени сила зависит обычно, когда ее изменяют путем регулирования, например, регулируют силу тяги самолета изменением режима работы ее двигателя. Силу, зависящую от координаты, можно создать сжатием или растяжением пружины или с помощью других упругих тел путем их деформации. Силы, зависящие от скорости движения, - это прежде всего силы сопротивления, когда материальная точка движется в какой либо среде, например, в воздухе, воде, масле.
Следует отметить, что в более общих случаях, если сила одновременно зависит от времени, координаты и скорости, в большинстве случаев дифференциальные уравнения можно проинтегрировать лишь приближенно, используя методы численного интегрирования.
Ниже рассмотрим примеры на составления и интегрирования дифференциального уравнения прямолинейного движения точки. Эти примеры позволяют выявить некоторые особенности решения таких задач.






