по дисциплине «Линейная алгебра» 1 курс 1 семестр

КОНТРОЛЬНАЯ РАБОТА.

Задание 1. Произвести следующие действия над матрицами: а) А+В; б) А^Т-В; в) А·В; г) α·А, α·В; д) записать А·В – α·В:

№ в-та	Данные задачи	№ в-та	Данные задачи
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;

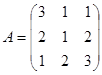
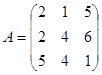
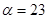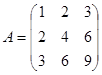
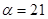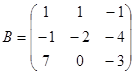
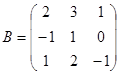
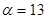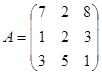
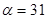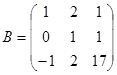
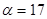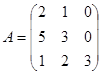
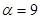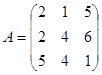
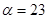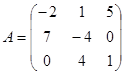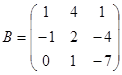
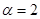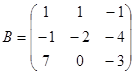
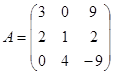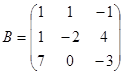
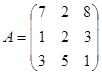
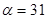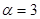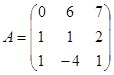
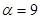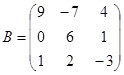
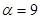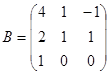
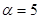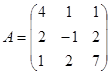
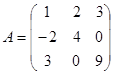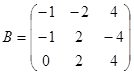
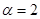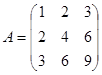
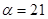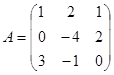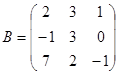
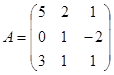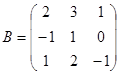
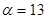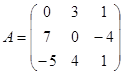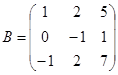
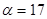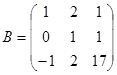
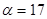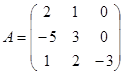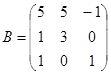
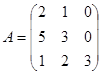
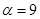Задание 2. Проверить совместность системы уравнений и в случае совместности решить ее А) по формулам Крамера; Б) методом обратной матрицы.

 

Вариант
Систе ма	2х1 + х2 + 3х3 = 7 2х1 + 3х2 + х3 = 1 3х1 +2х2 + х3 = 6	2х1 – х2 +2х3 = 3 х1 + х2 + 2х3 = -4 4х1 + х2 + 4х3 = -3	3х1 – х2 + х3 = 12 х1 + 2х2 + 4х3 = 6 5х1 + х2 + 2х3 = 3	2х1 – х2 + 3х3 = -4 х1 + 3х2 – х3 = 11 х1 – 2х2 + 2х3 = -7	3х1 – 2х2 + 4х3=12 3х1 + 4х2 – 2х3 =6 2х1 – х2 – х3 = - 9	8х 1+ 3х2 – 6х3 =-4 х1 + х2 – х3 = 2 4х1 + х2 – 3х3 =-5

 

Вариант
Система	4х1 + х2 – 3х3 = 9 х1 + х2 – х3 = -2 8х1 + 3х2 – 6х3 =12	2х1+3х2+4х3=33 7х1-5х2=24 4х1+11х3=39	2х1+3х2+4х3=12 7х1-5х2+х3=-33 4х1+х3=-7	х1+4х2-х3=6 5х2+4х3=-20 3х1-2х2+5х3=-22	3х1-2х2+4х3=21 3х1+4х2-2х3=9 2х1-х2-х3=10	3х1-2х2-5х3=5 2х1+3х2-4х3=12 х1-2х2+3х3=-1

 

Вариант
Систе ма	4х1+х2+4х3=19 2х1-х2+2х3=11 х1+х2+2х3=8	2х1-х2+2х3=0 4х1+х2+4х3=6 х1+х2+2х3=4	2х1-х2+2х3=8 х1+х2+2х3=11 4х1+х2+4х3=22	2х1-х2-3х3=-9 х1+5х2+х3=20 3х1+4х2+2х3=15	2х1-х2-3х3=0 3х1+4х2+2х3=1 х1+5х2+х3=-3	-3х1+5х2+6х3=-8 3х1+х2+х3=-4 х1-4х2-2х3=-9

 

 

Вариант
Систе ма	3х1+х2+х3=-4 -3х1+5х2+6х3=36 х1-4х2-2х3=-19	3х1-х2+х3=-11 5х1+х2+2х3=8 х1+2х2+4х3=16	3х1-х2+х3=9 5х1+х2+2х3=11 х1+2х2+4х3=19	2х1+3х2+х3=4 2х1+х2+3х3=0 3х1+2х2+х3=1	2х1+3х2+х3=12 2х1+х2+3х3=16 3х1+2х2+х3=8	х1-2х2+3х3=14 2х1+3х2-4х3=-16 3х1-2х2-5х3=-8

 

Вариант
Систе ма	3х1+4х2-2х3=11 2х1-х2-х3=4 3х1-2х2+4х3=11	х1+5х2-6х3=-15 3х1+х2+4х3=13 2х1-3х2+х3=9	4х1-х2=-6 3х1+2х2+5х3=-14 х1-3х2+4х3=-19	5х1+2х2-4х3= -16 х1+3х3= -6 2х1-3х2+х3=9	х1+4х2-х3=-9 4х1-х2+5х3=-2 3х2-7х3=-6	7х1+4х2-х3=13 3х1+2х2+3х3=3 2х1-3х2+х3=-10

 

 

Задание № 3. Найти общее решение и фундаментальную систему решений однородной системы линейных уравнений.

 

Вариант
Систе ма	х1+х2+х3=0 2х1-3х2+4х3=0 4х1-11х2+10х3=0	3х1-х2+2х3=0 х1+х2+х3=0 х1+3х2+3х3=0	х1+3х2+2х3=0 2х1-х2+3х3=0 3х1-5х2+4х3=0	4х1-х2+10х3=0 х1+2х2-х3=0 2х1-3х2+4х3=0	2х1+5х2+х3=0 4х1+6х2+3х3=0 х1-х2-2х3=0	3х1-х2-3х3=0 2х1+3х2+х3=0 х1+х2+3х3=0	х1-х2+2х3=0 2х1+х2-3х3=0 3х1+2х3=0

 

Вариант
Систе ма	2х1-х2-5х3=0 х1+2х2-3х3=0 5х1+х2+4х3=0	5х1-5х2+4х3=0 3х1+х2+3х3=0 х1+7х2-х3=0	х1+3х2-х3=0 2х1+5х2-2х3=0 х1+х2+5х3=0	2х1+х2+3х3=0 3х1-х2+2х3=0 х1+3х2+4х3=0	х1-2х2-х3=0 2х1+3х2+2х3=0 3х1-2х2+5х3=0	2х1+х2-х3=0 3х1-2х2+4х3=0 х1-5х2+3х3=0	4х1+х2+3х3=0 8х1-х2+7х3=0 2х1+4х2-5х3=0

 

Вариант
Систе ма	х1+4х2-3х3=0 2х1+5х2+х3=0 х1-7х2+2х3=0	х1-2х2+х3=0 3х1+х2+2х3=0 2х1-3х2+5х3=0	х1+2х2+3х3=0 2х1-х2-х3=0 3х1+3х2+2х3=0	3х1+2х2=0 х1-х2+2х3=0 4х1-2х2+5х3=0	2х1-х2+3х3=0 х1+2х2-5х3=0 3х1+х2+х3=0	3х1+2х2-х3=0 2х1-х2+3х3=0 4х1+3х2+4х3=0	х1-3х2-4х3=0 5х1-8х2-2х3=0 2х1+х2-х3=0

 

Вариант
Систе ма	3х1+5х2-х3=0 2х1+4х2-3х3=0 х1-3х2+х3=0	3х1-2х2+х3=0 2х1-3х2+2х3=0 4х1+х2-4х3=0	7х1+х2-3х3=0 3х1-2х2+3х3=0 х1-х2+2х3=0	х1+2х2-4х3=0 2х1-х2-3х3=0 х1+3х2+х3=0	7х1-6х2+х3=0 4х1+5х2=0 х1-2х2+3х3=0	5х1-4х2+2х3=0 3х2-2х3=0 4х1+х2-3х3=0	6х1+5х2-4х3=0 х1+х2-х3=0 3х1+4х2+3х3=0

 

Вариант
Систе ма	8х1+х2-3х3=0 х1+5х2+х3=0 4х1-7х2+2х3=0	х1+7х2-3х3=0 3х1-5х2+х3=0 3х1+4х2-2х3=0

 

Задание № 4. Исследовать систему линейных уравнений, для совместной системы найти общее и одно частное решение.

 

Вариант
Система	х1+2х2=1 -х2+х4+х5=4 3х1-х3+2х5=2	2х1+3х2+х4=6 х2-х3=4 -3х1-х3-х5=2	2х1-х3-х4=4 х2+3х3+2х4=3	2х1+х3= -5 -х1+х2=3 3х1-х4=1	х1+2х4-2х5=4 -х3-3х4+х5=5 х2+3х5= -2	х1+х2+х3+х4+х5=5 х1-х2+х3-х4+х5=1	х1-2х2+х3+х4=1 х1-2х2+х3-х4= -1

 

Вариант
Система	х1-2х2+х3-х4=-1 х1-2х2+х3+5х4=5	х1+х2+х3+х4=4 -х1+х2+х3+х4=3	х1+х2+х3+х4+х5=1 х1+х3+2х5=4	х1-2х2+х3+х4=1 х1-2х2+х3+5х4 =5	х1-х2+х3+х4=4 х1-х2+х3-2х4=0	х1+2х2+2х3+х4=2 2х1+х2+х3-2х4 =6	х1+х4=2 х1+х2+х3=3

 

Вариант
Система	х1+х2+х3+х4+х5=1 х1+х3+2х5=4 х2+х4= -2	х1+х2+х3-х4+х5=5 х1+х3+2х5=4 х2-х4=0	6х1+3х2+4х3-3х4+4х5 =5 4х1+2х2+х3-2х4+3х5=4	х1-2х2+3х3+2х4+х5=4 3х1-6х2+5х3+4х4+3х5 =5	4х1+2х2+3х3-2х4+4х5 =0 6х1+3х2+2х3-3х4+4х5 =5	х1-2х2+7х3+4х4+х5 =11 х1-2х2+3х3+2х4+х5 =4

 

Вариант
Система	2х1-х2-х3+2х4+3х5=2 6х1-3х2-2х3+4х4+5х5 =3	6х1-3х2-4х3+8х4+13х5 = 9 2х1-х2-х3+2х4+3х5 =2	х1+х2+х3+х4=1 х2+х3+х4=1 х3+х4=1	-х1-2х2+х3+х4=1 -2х1+х2+х3+х4=2 3х1+2х4=3	х1+2х2-х3+х4=3 х1+4х2+х3= -2	2х1+х2-х3+х4=3 -2х1+х2+х3-х4= -1

 

Вариант
Система	х1+х2+х3+х4+х5=5 х2+х3+х4-х5=2 х3-х4+х5=1	х1+х2+х3+5х4=0 х1+х2-х4=3 х1-х2+3х4= -1	х1+х2+х3+2х4=7 х2+х3+х4=5 х1-х4=3	х1+2х2-х4=3 х1-х2+3х4= -1 2х1+х2+х3-х4=5

 

Задание 5. На плоскости относительного некоторого базиса даны координаты трех векторов:

При N – четном:

При N – нечетном: .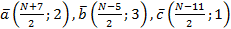

N- номер варианта по списку.

 

1. Найти координаты векторов .

2. Проверить, что векторы и 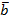образуют базис на плоскости. Найти координаты вектора в этом базисе.

3. Определить при каком значении параметра α векторы и 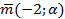будут коллинеарными.

4. Найти координаты вектора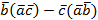

5. Вычислить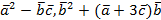

6. Найти косинус угла между векторами и .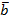

Задание 6. Даны вершины треугольника A, B, C. Найти:

 

1) длины сторон AC и BC;

2) уравнение прямой, на которой лежит сторона AB;

3) уравнение прямой, на которой лежит высота, проведённая из точки C;

4) длину этой высоты;

5) уравнение прямой, на которой лежит медиана, проведённая из точки C;

6) длину этой медианы;

7) уравнение прямой, которая проходит через точку A и параллельна прямой, на которой лежит медиана, проведённая из точки C;

8) площадь треугольника;

9) угол C.

 

№	Координаты вершин	№	Координаты вершин	№	Координаты вершин
	A(2;-2), B(3;5), C(6;1)		A(3;2), B(5;-6), C(1;-4)		A(-2;2), B(3;-5), C(6;-1)
	A(1;4), B(0;-4), C(-3;-2)		A(1;6), B(2;7), C(-5;3)		A(2;4), B(0;-4), C(3;2)
	A(0;-3), B(1;4), C(4;0)		A(-3;4), B(2;-4), C(-1;0)		A(0;-3), B(1;-4), C(4;2)
	A(4;5), B(3;-3), C(0;-1)		A(-3;-1), B(-2;6), C(0;2)		A(3;5), B(3;-3), C(1;-1)
	A(3;-4), B(4;3), C(7;-1)		A(1;5), B(-2;-3), C(5;-1)		A(3;4), B(4;3), C(7;1)
	A(3;2), B(2;-6), C(-1;-4)		A(2;-2), B(3;6), C(6;1)		A(-3;2), B(2;-0), C(-1;-4)
	A(1;0), B(2;7), C(5;3)		A(7;4), B(0;-4), C(3;-2)		A(1;0), B(2;-7), C(-5;3)
	A(3;4), B(2;-4), C(-1;-2)		A(0;-3), B(1;-4), C(4;0)		A(3;0), B(2;-4), C(-1;-2)
	A(-3;-1), B(-2;6), C(1;2)		A(4;-5), B(3;-3), C(0;-1)		A(3;-1), B(-2;-6), C(1;2)
	A(-1;5), B(-2;-3), C(-5;-1)		A(3;-4), B(4;-3), C(7;-1)		A(-1;0), B(-2;-3), C(-5;-1)

 

Задание 7. Построить кривые по заданным уравнениям.

 

№	Уравнения		№	Уравнения
	(х-2)2 + (у-3)2=9, у2 = 9х, 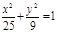, .		(х-3)2 + (у-2)2=9, у2 = -4х, ;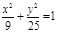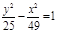
	(х+3)2 + (у-5)2=4, у2=7х, 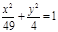,		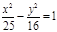(х-5)2 + (у+3)2=4, у2 = -2х, ;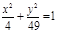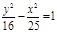
	(х+1)2 + (у-2)2=16, у2=5х, ,		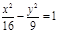(х+1)2 + (у+1)2=16, у2 = -6х, ;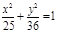
	(х-3)2 + (у+4)2=25, у2 = 16х, 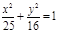,		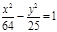(х+4)2 + (у-3)2=25, у2 = -х, ;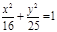
	(х+3)2 + (у+3)2=4, у2 = 3х, 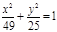;		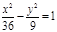(х-3)2 + (у-3)2=4, у2 = -8х, ;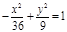
	(х-1)2 + (у+1)2=1, у2 = 4х, ;		(х+1)2 + (у-1)2=1, х2= 9у; ;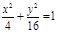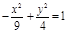
	(х+2)2 + (у-1)2=36, у2 = 2х, 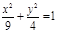;		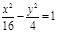(х-1)2 + (у+2)2=36, х2= 7у; ;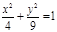
	(х-4)2 + (у+2)2=49, у2 = 6х, 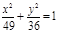;		(х+2)2 + (у-4)2=49, х2= 5у; ;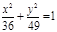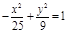
	(х+4)2 + (у-4)2=9, у2 = х, 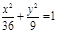;		(х-4)2 + (у+4)2=9, х2= 16у; ;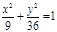
	(х-5)2 + (у+1)2=4, у2 = 8х, ;		(х+1)2 + (у-5)2=4, х2= 3у; ;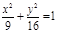
	(х+5)2 + (у-6)2=16, у2 = -9х, ;		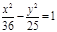(х-6)2 + (у+5)2=16, х2= 4у; ;
	(х-1)2 + (у+5)2=1, у2 = -7х, ;		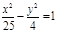(х+5)2 + (у-1)2=1, х2= 2у; ;
	(х+1)2 + (у-3)2=25, у2 = -5х, 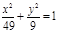;		(х-3)2 + (у+1)2=25, х2= 6у; ;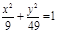
	(х-3)2 + (у-2)2=36, у2 = -16х, 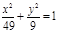;		(х-2)2 + (у-3)2=36, х2= у; ;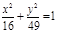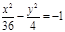
	(х+2)2 + (у+4)2=49, у2 = -3х, 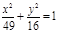;		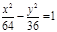(х+4)2 + (у+2)2=49, х2= 8у; 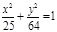;