Аннуитет
Аннуитет - это серия равновеликих платежей (поступлений), отстоящих друг от друга на один и тот же промежуток времени.
Принято различать обычный и авансовый аннуитеты.
В том случае, если платежи (поступления) производятся в конце каждого периода, говорят об обычном аннуитете. Если же платежи (поступления) осуществляются авансом, т. е. в начале каждого периода, говорят об авансовом аннуитете.
Расчёт текущей стоимости обычного аннуитета.
Базовые формулы:
а) при платежах (поступлениях) в конце каждого года:
где РМТ - равновеликие периодические платежи (поступления);
фактор текущей стоимости обычного аннуитета при платежах (поступлениях) в конце каждого года;
б) при более частых, чем 1 раз в год, платежах (поступлениях):
где 
фактор текущей стоимости обычного аннуитета при более частых, чем 1 раз в год, платежах (поступлениях);
-число начислений раз в году
Расчёт текущей стоимости авансового аннуитета.
Базовые формулы:
а) при платежах (поступлениях) в начале каждого года:
 |
б) при более частых, чем 1 раз в год, платежах (поступлениях):
 |
Расчёт будущей стоимости обычного аннуитета.
Базовые формулы.
а) при платежах (поступлениях), осуществляемых 1 раз в конце года:
где 
– фактор накопления денежной единицы за период при платежах (поступлениях), осуществляемых 1 раз в конце года;
б) при платежах (поступлениях), осуществляемых чаще, чем 1 раз в год:
где 
фактор накопления денежной единицы за период при платежах (поступлениях), осуществляемых чаще, чем 1 раз в год;
Расчет будущей стоимости авансового аннуитета. Базовая формула:
 |
а) при платежах (поступлениях), осуществляемых 1 раз в начале года:
где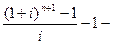 
фактор накопления денежной единицы за период при платежах (поступлениях), осуществляемых 1 раз в начале года;
б) при авансовых платежах (поступлениях), осуществляемых чаще, чем 1 раз в год:
 |
где 
- фактор накопления денежной единицы за период при авансовых платежах (поступлениях), осуществляемых чаще, чем 1 раз в год.
Амортизация кредитов
Для определения аннуитетных (регулярных равновеликих) платежей в счет погашения кредита, выданного на определенный период при заданной ставке по кредиту используется функция взноса на амортизацию кредита.
Базовые формулы:
а) при платежах (поступлениях), осуществляемых 1 раз в год:
где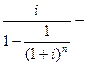 
фактор взноса на амортизацию единицы при платежах (поступлениях), осуществляемых 1 раз в год;
б) при платежах (поступлениях), осуществляемых чаще, чем 1раз в год:
где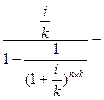 
фактор взноса на амортизацию единицы при платежах (поступлениях), осуществляемых чаще, чем 1 раз в год.
Многие займы, такие как кредиты на покупку дома и покупку машины, выплачиваются равномерными периодическими платежами. Каждый из них состоит из двух частей: процентов на остаток долга и части его основной суммы. После каждой выплаты оставшаяся сумма долга уменьшается на уже выплаченную величину. Следовательно, в следующих платежах та часть, которая содержит в себе начисленные проценты, меньше, чем проценты за предыдущий период, а часть, приходящаяся на выплату основной суммы займа, больше, чем в предыдущем периоде.
Допустим, вы берете кредит в 100000 долл. на покупку дома под 9% годовых на условиях выплаты всей суммы с процентами тремя ежегодными платежами.
Сначала мы рассчитываем годовой платеж, для чего находим PMT, PV которого составляет 100000 долл. при условии уплаты 9% годовых на протяжении трех лет:
Таким образом, годовой платеж составляет 39505,48 долл.
Далее необходимо определить, какую часть от 39505,48 долл. в первый год составят проценты и сколько придется на долю основного платежа? Поскольку процентная ставка равна 9% годовых, часть, приходящаяся на проценты в первый год, должна быть 0,09 х 100000, или 9000 долл. Остаток от 39504,48 долл., или 30505,48 долл. — сумма платежа от основной суммы в 100000 долл. Таким образом, после первого платежа остаток долга по займу составляет 100000 долл. - 30505,48 долл., или 69 494,52 долл. Процесс постепенной регулярной выплаты займа на протяжении всего его периода называется амортизацией займа.
Далее рассчитаем платежи во второй год. Процентные платежи во второй год составят 0.09 х 69 494,52 долл., или 6254,51 долл. Остаток от 39504,48 долл. после расчета процентов составит 33250,97 долл. — это выплата основной суммы. Остаток после второй выплаты, следовательно, равен 69494,52 долл. - 33250,97 долл., или 36243,54 долл.
Третий и последний платеж покрывает как проценты, так и основную сумму 36243,54 долл. (т.е. 1,09 х 36243,55 долл. = 39504,47 долл.). Рассмотренный график погашения трехгодичного займа представлен в таблице.
| Год | Начальный долг | Общий платеж | Выплаченные проценты | Выплаченная основная сумма | Остаток долга |
| Итого |
Анализ представленных данных показывает, что с каждой последующей выплатой 39504,48 долл. часть, приходящаяся на проценты, уменьшается, а часть основной суммы, предназначенной для выплаты основной суммы займа, увеличивается.
Формирование фонда возмещения
Для определения равномерных периодических платежей, которые необходимо осуществлять в течение заданного периода, чтобы к концу срока иметь на счете, приносящем доход по заданной ставке, определенную сумму денег, используется функция формирования фонда возмещения.
Базовые формулы:
а) при платежах (поступлениях), осуществляемых 1 раз в год:
где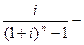 
фактор фонда возмещения при платежах (поступлениях), осуществляемых 1 раз в год;
б) при платежах (поступлениях), осуществляемых чаще, чем 1раз в год:
где 
фактор фонда возмещения при платежах (поступлениях), осуществляемых чаще, чем 1 раз в год.
