1.Непрерывные функции.
Теорема 1. Всякая непрерывная на отрезке [a,b] функция интегрируема на этом отрезке.
2.Монотонные ограниченные функции и некоторые другие классы интегрируемых функций.
Теорема 2. Любая монотонная ограниченная функция является интегрируемой функцией.
Теорема 3. Любая ограниченная функция, имеющая конечное число разрывов интегрируема.
Билет 37. Замена переменной и интегрирование по частям в определенном интеграле.
Формула замены переменной. Пусть х = φ(t) непрерывна и диф. на T = {α; β}. Функция f(x) непрерывна на отрезке [a; b] = [x(α); x(β)]. Тогда ∫f(x)dx (a; b) = ∫f(φ(t))*φ’(t)dt (α; β)
Интегрирование по частям. Пусть U(x) и V(x) непрерывны и диф. на отрезке [a; b]. Тогда имеет место формула: ∫UdV = UV|ab - ∫VdU
Доказательство: такое же как в неопр. интеграле
Билет 38. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
Интеграл с переменным верхним пределом. Если функция f(x) непрерывна на [a; b], то для всех х (- [a; b] определена функция Ф(х) = ∫f(t)dt (a; x), которая называется интегралом с переменным верхним пределом. На интеграл с переменным верхним пределом распространяются все правила и свойства определённого интеграла.
Теорема. Если f(x) непрерывна на [a; b], то Ф’(x) = (∫f(t)dt)’ (a; x) = f(x), для всех х (- [a; b]
Формула Ньютона-Лейбница. Пусть f(x) непрерывна на [a; b], F(x) – какая либо первообразная для неё, тогда:
∫f(x)dx = F(x)|ab = F(b) – F(a)
Билет 39. Несобственные интегралы 1-го и 2-го рода. Сходящиеся и расходящиеся интегралы. Геометрический смысл.
Определение. При введении понятия определённого интеграла предполагали следующие условия: а) отрезок интегрирования [a; b] является конечным; б) подынтегральная функция f(x) – ограничена на отрезке интегрирования. В этом случае интеграл называется собственным. Если хотя бы одно из указанных условий нарушается, то интеграл называется несобственным, т.е. ∫f(x)dx называется несобственным, если а=-∞ или b=+∞ (или невзаимоискл.)
Сходимость / расходимость. Пусть f(x) определена и непрерывна на [a; b] (b>a). Обозначим I(b) = ∫f(x)dx, фиксируя нижний предел а. Функцию I(b) рассмотрим как интеграл с переменным верхним пределом.
1) ∫f(x)dx (a; +∞) = lim ∫f(x)dx (a;b) (bà+∞) – несобственный интеграл 1 рода на [a; +∞). Если предел в правой части существует и конечен, тогда несобственный интеграл сходится. В противном случае расходится.
2) ∫f(x)dx (-∞; b) = lim ∫f(x)dx (a;b) (aà-∞)
3) ∫f(x)dx (-∞; ∞) = ∫f(x)dx (-∞; c) + ∫f(x)dx (c; +∞) = пределы
Геометрический смысл. Пусть f(x)>0. Несобственный интеграл определяет площадь под кривой в соотв. пред., в данном случае [a; + ∞)
Несобственный интеграл 2го рода. Пусть функция f(x) задана на [a; b), не ограничена при
xàb и для любого ε>0 найдётся ∫f(x)dx (a; b-ε). Несобственным интегралом 2го рода от функции
f(x) называется lim ∫f(x)dx (a; b-ε) (εà0+) = ∫f(x)dx (a; b)
Геометрический смысл: также только площадь под графиком.
Билет 40. Свойства несобственных интегралов. Признаки сходимости. Эталонные ряды.
Свойства. 1) Если сходится несобственный интеграл ∫f(x)dx (a; ∞), то найдётся такая b>a, что несобственный интеграл будет сходится и ∫f(x)dx (a; ∞) = ∫f(x)dx (b; a) + ∫f(x)dx (b; ∞)
2)Если сходятся интегралы ∫f(x)dx (a; ∞) и ∫g(x)dx (a; ∞), то сходятся и интегралы ∫(αf(x)+-βg(x))dx (a; ∞), где α и β=const и <M.
Признаки сходимости.
1) Признак сравнения. Пусть даны два несобственных интеграла ∫f(x)dx (a; ∞) и ∫g(x)dx (a; ∞), подынтегральные функции которых удовлетворяют неравенству: 0 <= f(x) <=g(x), для всех a <= x <∞. Тогда из сходимости второго интеграла следует сходимость первого, а из расходимости первого – расходимость второго.
Доказательство:
Для всех b (- (a; +∞) интеграл ∫f(x)dx (a; b) <= ∫g(x)dx (a; b). а) Перейдём к пределу при bà∞. По теореме о предельных переходах в неравенстве существует предел: lim ∫f(x)dx (a; b) (bà∞). Существование этого предела эквивалентно существованию интеграла. б) Аналогично из расходимости 1го интеграла вытекает несуществование пределов ∫f(x)dx (a; b) (bà∞) и ∫g(x)dx (a; b) (bà∞)
2) Предельный признак сравнения (эквивалентности?). Пусть существует lim f(x)/g(x) (xà+∞) = A < +∞. Тогда интегралы f(x) и g(x) сходятся или расходятся одновременно.
3) Признак Дирихле (условной сходимости). Если 1) Функции f(x) и g(x) определены в a <= x <= ∞; 2) f(x) – интегрируема в [a; A] и F(A) – ограниченная функция; 3) g(x) не возрастает и её предел при хà∞ равен нулю, то ∫f(x)g(x)dx (a; ∞) сходится
Эталонным называется интеграл, который сходится на одном промежутке, а расходится на другом.
Билет 41. Нахождение площади плоской фигуры.
1) В прямоугольных координатах.
Если непрерывная кривая задана в прямоугольных координатах уравнением y = f(x) (f(x) >= 0), то площадь криволинейной трапеции, ограниченной этой кривой двумя вертикальными прямым x=a, x=b, осью абцисс, определяется формулой S = ∫f(x)dx
2) В полярных координатах
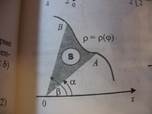
Если непрерывная кривая задана в полярных координатах уравнением ρ=ρ(φ), то площадь сектора AOB, ограниченная дугой кривой и двумя полярными радиусами OA и OB, выразится интегралом S = ½ ∫(ρ(φ))2dφ
3) 
В параметрической форме.
S = ∫ψ(t)*φ’(t)dt, где x = φ(t), y = ψ(t)
Билет 42. Нахождение объема тела вращения.
a) Объём тела, образованного вращением вокруг оси Ох криволинейной трапеции, ограниченной кривой, заданной уравнением y = y(x), где y(x) - непрерывная однозначная функция на [a; b], осью Ох и прямыми x=a и x=b вычисляется по одной из формул: Vx = П∫f 2(x)dx (a; b) или
Vx = П ∫f 2(x)*x’(y)dy (c; d)
б) Объём тела, образованного вращением вокруг оси Оy криволинейной трапеции,
ограниченной кривой, заданной уравнением x = x(y), где x(y) - непрерывная
однозначная функция на [с; d], осью Оy и прямыми y=c и y=d вычисляется по
одной из формул: Vy = П∫f 2(y)dy (c; d) или Vy = П ∫x2*y’(x)dx
Билет 43. Длина дуги кривой.
a)В прямоугольных координатах.
Пусть на [a; b] y=f(x) диффер. è непрерывна. Тогда существует предел: l = ∫корень из 1+(y’)2dx
б) В параметрической форме.
Пусть дуга задана параметрическими уравнениями x=x(t), y=y(t), x <= t <= β, то длина дуги кривой равна:
l = ∫кор. x’2(t)+y’2(t)dt, (t1; t2) – значения параметра, соответствующие концам дуги
в) В полярной системе
Если кривая задана в полярных координатах уравнением ρ=ρ(φ), φ (- [α; β], то длина дуги кривой
l = ∫корень из ρ2(φ)+ ρ’2(φ)dφ (α; β) – значения полярного угла в крайних точках дуги.
Билет 44. Определенный интеграл
Определённым интегралом от непрерывной функции f (x) на конечном отрезке [ a, b ] (где 
) называется приращение какой-нибудь её первообразной на этом отрезке. При этом употребляется запись
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [ a, b ] – отрезком интегрирования.
