Стандартное нормальное распределение -это особая форма распределения, которую можно использовать в качестве стандарта при оценках любых данных, независимо от их размерности. По-другому такое распределение называют нормированным нормальным распределением.
Введение стандартного нормального распределения вызвано тем, что обычная формула общего нормального распределения для практического применения неудобна. По этой формуле положение кривой по горизонтали, ее размер и форма определяются и зависят от объема совокупности, значения средней арифметической и стандартного отклонения.
Чтобы получить вместо большого числа кривых одну унифицированную кривую были проделаны следующие шаги:
1. Всю площадь под кривой приняли за единицу.
2. Стандартное отклонение приняли за единицу.
3. Сместили оси координат так, чтобы среднее арифметическое стало равным нулю.
4. Ввели новую переменную z и назвали ее стандартной нормальной переменной. Данной переменной соответствует следующая формула ее вычисления:
При этих условиях функция от x общего теоретического нормального распределения 
преобразуется в функцию от z с "единичным" объемом совокупности, "единичным" стандартным отклонением и «нулевым» средним арифметическим.
Эта функция называется стандартным нормальным распределением, которой соответствует формула:
В этой формуле: средняя арифметическая равна нулю (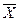
, μ = 0);
стандартное отклонение равно единице (σ, s = 1);
объем совокупности равен единице (N, n= 1 ).
Формуле стандартного распределения соответствует стандартная нормальная кривая, в которой значение средней арифметической совпадает с началом координат, а по горизонтали откладываются единицы стандартной нормальной переменной.
Кривая стандартного нормального распределения
Y
z
-3 -2 -1 0 1 2 3 Z
Для стандартного нормального распределения существуют «зэт-таблицы», которые связывают значения «зэт» с площадью между «нулевой» средней арифметической и конкретными значениями «зэт».
На основе стандартного нормального распределения и «зэт-таблиц» решаются следующие практически важные задачи:
1. Определение доли или количества объектов, расположенных внутри интервала с границами Z1 и Z2.
2. Определение доли или числа объектов со значениями признака Z2 и больше.
3. Определение доли или числа объектов со значениями признака Z1 и меньше.
Этим трем задачам соответствуют под кривой площади с /1/, /2/, и /3/ штриховкой.
Z1 Z2
Также как и для общего теоретического нормального распределения, для стандартного распределения:
68,3% площади под кривой соответствует 
95,5% площади под кривой соответствует 
99,7% площади под кривой соответствует 
Алгоритм использования «зэт-таблицы» S=f(Z).
1. Для данной совокупности вычислить объем N, среднюю арифметическую 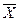, стандартное отклонение σ, если они не даны.
2. Для заданных граничных значений Xi определить Zi по формуле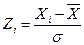 
.
3. Обратиться к «зэт-таблице» и по вычисленному значению Zi определить площадь Si под кривой между средней арифметической и данным «зэт».
4. Если требуется, определить сумму или разность площадей S1 и S2 внутри граничных значений «зэт» или за их пределами.
5. По найденной доле вычислить соответствующий ей процент вариантов (если требуется по условиям задачи/)и сделать вывод.
ТАБЛИЦА ЗНАЧЕНИЙ ДОЛИ ПЛОЩАДИ ПОД КРИВОЙ
| Z | S | Z | S | Z | S | Z | S | Z | S | Z | S |
| 0,0 | 0,0000 | 0,5 | 0,1915 | 1,0 | 0,3413 | 1,5 | 0,4332 | 2,0 | 0,4772 | 2,5 | 0,4938 |
| 0,1 | 0,0398 | 0,6 | 0,2257 | 1,1 | 0,3643 | 1,6 | 0,4452 | 2,1 | 0,4821 | 2,6 | 0,4953 |
| 0,2 | 0,0793 | 0,7 | 0,2580 | 1,2 | 0,3849 | 1,7 | 0,4554 | 2,2 | 0,4861 | 2,7 | 0,4961 |
| 0,3 | 0,1179 | 0,8 | 0,2881 | 1,3 | 0,4032 | 1,8 | 0,4641 | 2,3 | 0,4893 | 2,8 | 0,4974 |
| 0,4 | 0,1554 | 0,9 | 0,3159 | 1,4 | 0,4192 | 1,9 | 0,4713 | 2,4 | 0,4918 | 2,9 | 0,4981 |
| 3,0 | 0,4986 |
