Рассмотрим сущность этих методов на и примере простейшего линейного измерительного преобразователя (ИП). Его реальная статическая характеристика имеет вид
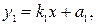
где х и 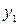 – соответственно входной и выходной информативные сигналы ИП; k и а1 – параметры ИП.
– соответственно входной и выходной информативные сигналы ИП; k и а1 – параметры ИП.
В процессе эксплуатации параметры отклоняются от номинальных значений  и
и  ;
; 
 что при фиксированном уровне x; вызывает погрешность ИП, приведенное значение которой
что при фиксированном уровне x; вызывает погрешность ИП, приведенное значение которой

где  – нормирующий множитель, равный изменении сигнала у при изменении х в пределах от 0 до хmax;
– нормирующий множитель, равный изменении сигнала у при изменении х в пределах от 0 до хmax;  и
и  – относительные изменения параметров ИП.
– относительные изменения параметров ИП.
В последнем выражении первое слагаемое отражает мультипликативную, второе – аддитивную составляющие погрешности. Усложним теперь исходную структуру, включив параллельно ИП1 идентичный сравнительный преобразователь (рис. 3.1.7.3 а). Если выходной сигнал ИП2 вычитается из выходного сигнала ИП1, то такой составной ИП называется дифференциальным. Его статическая характеристика имеет вид

где х0 – значение меры или стандартного образца, подаваемого на вход ИП2.
Приведенная погрешность дифференциального ИП имеет вид
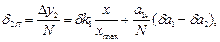
где 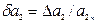 .
.
При вычислении принято:  ;
; 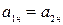 (но из-за действия помех
(но из-за действия помех 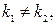
 ); х0 = 0.
); х0 = 0.
Сравнив полученные выражения, заключаем, что в сопоставимых условиях мультипликативные погрешности дифференциального и одноканального ИП одинаковы. Что касается аддитивной погрешности, то здесь несомненное преимущество имеет дифференциальный ИП, в котором за счет сравнительного канала удается уменьшить, а при полной корреляции случайных величин  и
и  в принципе полностью подавить аддитивные составляющие случайной и систематической погрешностей.
в принципе полностью подавить аддитивные составляющие случайной и систематической погрешностей.
Охватим ИП1 цепью отрицательной обратной связи (рис. 3.1.7.3 б). Статическая характеристика такого ИП имеет вид

где ko — коэффициент преобразования звена в цепи обратной связи.
Для упрощения записи принято, что  . Приведенная погрешность ИП с замкнутой структурной схемой
. Приведенная погрешность ИП с замкнутой структурной схемой
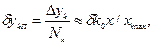
где 


Величина 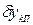 не зависит от
не зависит от 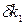 , т. е. введение отрицательной обратной связи позволяет практически устранить изменения коэффициента преобразования (т. е. мультипликативную погрешность) канала прямой передачи информации. Погрешности, возникающие в цепи обратной связи, в такой структуре не подавляются, поэтому ее применение оправдано при
, т. е. введение отрицательной обратной связи позволяет практически устранить изменения коэффициента преобразования (т. е. мультипликативную погрешность) канала прямой передачи информации. Погрешности, возникающие в цепи обратной связи, в такой структуре не подавляются, поэтому ее применение оправдано при  .
.
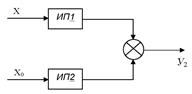
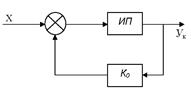
а) б)
Рис. 3.1.7.3 Структурные методы уменьшения погрешностей
Таким образом, в указанных условиях применение дифференциальных схем позволяет уменьшить аддитивные составляющие погрешности, а применение структур с обратной связью – мультипликативные составляющие погрешности.






