Составление блок-схемы решения задач

Для решения любой задачи на ЭВМ необходимо составить алгоритм решения задачи.

Под алгоритмом понимается совокупность правил и указаний достижения конечного результата.

Графическим выражением алгоритма является составленная блок - схема, которая отражает порядок выполнения необходимых расчетов на ЭВМ.

Для рассмотренной нами задачи – определение оптимальной высоты выемочной ступени – может быть два случая составления блок-схем.

1. Метод полного перебора всех вариантов.

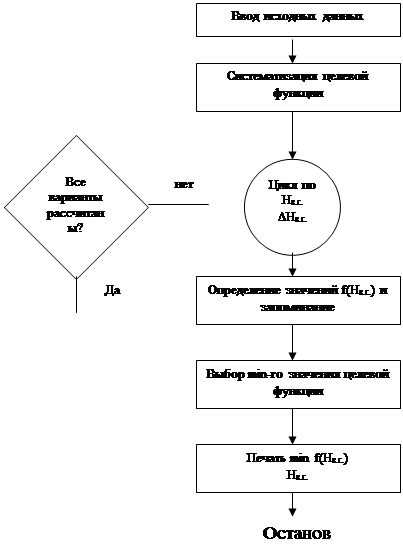В данном методе подробно рассмотрим порядок составления самой блок-схемы и всех процессов, происходящих в ЭВМ при определении минимального значения целевой функции. Блок-схема будет иметь следующий вид:

Блок – схема расчета оптимальной высоты выемочного участка (ступени).

 

Любое составление блок-схемы начинается с подготовки исходной информации, необходимой для ввода исходных данных в ЭВМ;

· Следующим этапом происходит систематизация целевой функции решаемой задачи;

· Цикл по Н_в.с – т.е. решение задачи по определению оптимальной высоты выемочной ступени – это значит, что будет произведен полный перебор вариантов, а затем определение значения целевой функции f(Н_в.с). Машина возьмет первое значение подставит его и определит, а затем вернется назад к повторному расчету.

ЭВМ команда о повторных расчетах может быть задана автоматически счетчиком цикла. Если это не подразумевается, то всегда нужно указывать логический блок – все ли варианты рассчитаны?

· Тогда в этом диапазоне можно просчитать n вариантов и получить n значений, но нам необходимо выбрать минимальное значение, т.е. нам необходимо произвести сравнение значений.

· ЭВМ определив последнее значение отнесет его на сумматор и с ним сравнивает каждую соседнюю точку, но так, что большее значение убирается, а на сумматоре остается меньшее значение их двух сравниваемых. Таким образом сравнение производится по всем точкам (обе ветви кривой графика), несмотря на то, что уже определено минимальное значение функции (нижняя точка искомого значения функции) так как ЭВМ не видит графика и сравнивает все точки.

· После выбора минимального значения целевой функции подается команда на печатное устройство для получения результата.

· После получения расчетного результата подается команда «остановить».

Такой алгоритм и естественно метод поиска оптимального значения обладает основным недостатком состоящем в том, что по сути дважды перебираются все варианты, а именно:

1-й раз при расчете самой целевой функции;

2-й раз при сравнении и выборе минимального значения.

Это оправдано для много экстремальных задач, где в принципе неизвестно положение истинного оптимума. Для одноэкстремальных задач или целевой функции количество рассматриваемых вариантов может быть существенно сокращено.

 

 

2. Метод направленного поиска экстремума целевой функции.

При решении наших задач необходимо искать экстремальное значение, т.к. задачи могут быть на определение минимального или максимального значения параметра.

Смысл этого метода состоит в том, чтобы считать значение целевой функции только слева от граничного значения параметра до оптимума или только справа – т.е. мы считаем варианты по одной или другой ветви имеющего графика зависимости.

(Здесь уже есть выгодное положение – например, для ЭВМ считать малое количество вариантов – 1000-10000 необходимо мало времени, ну, а если таких вариантов миллионы, то это уже ощутимо).

Рассмотрим ниже блок-схему направленного перебора вариантов при расчете оптимальной высоты выемочной ступени.

 

да

нет

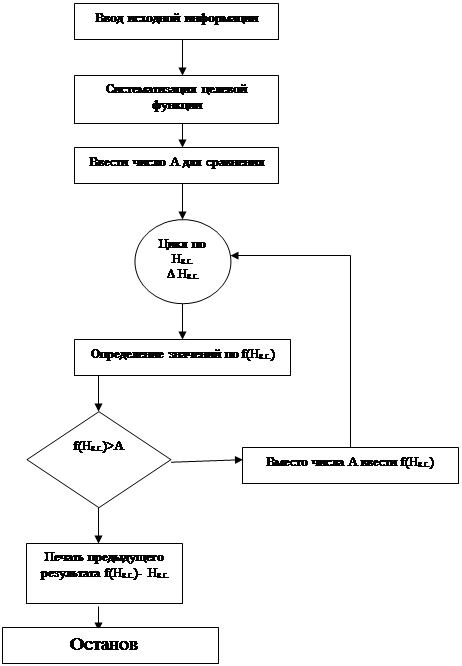Блок-схема расчета оптимальной высоты выемочной ступени (методом направленного перебора).

 

Если при полном переборе вариантов мы рассчитываем значения всех вариантов, то при направленном переборе мы будем сравнивать только полуветвь графика. Но ЭВМ это сравнение должна с чем-то сравнивать. Поэтому после систематизации целевой функции вводим новый блок.

Таким образом, для дальнейшего расчета, вводим число А для сравнения. Вводимое число должно быть в разумных пределах и оно может быть какое угодно, но больше целевой функции.

Число А должно быть как можно большим при минимальном значении функции и как можно меньшим при когда функция максимизируется.

Считаем цикл на ЭВМ и определяем значение функции, а затем полученный результат вводим в логический блок.

В логическом блоке производится сравнение f(Н_в.с) с числом А. Если число А меньше целевой функции, т.е. «нет» производится повторный расчет и вместо числа запишем f(Н_в.с).

Если «да» даем печатать предыдущее значение f(Н_в.с) и получив его даем команду ЭВМ – останов.

(Число А необходимо 1-й раз, так как сравнив его со вторым числом мы большее отбрасываем и оставляем меньшее, т.е. 2-е число. И так производим дальнейшее сравнение пока не получим минимальное значение, т.е. приходим в точку оптимума.

Так, например, f(Н_в.с) =12,7; f₂ =11,5; f₃ =10,8, то приняв число А =10⁴⁰ мы отбрасываем и берем 12,7, а затем 11,5; 10,8 и минимальное значение).

Таким образом, по такому алгоритму мы посчитаем только половину вариантов – этот алгоритм представляется как направленный (метод перебора).