4.1 Проверка гипотезы по критерию Пирсона
Критерий Пирсона (критерий хи-квадрат) считается наиболее удобным и универсальным. Он может быть использован для проверки допущения о любом распределении, даже в том случае, если не известны значения параметров распределения. Главный недостаток критерия - его нечувствительность к обнаружению адекватного распределения в случае, когда выборка невелика.
Критерий записывается в виде следующего альтернативного условия, отвечающего левосторонней критической области:
 - гипотеза принадлежности опытных данных
- гипотеза принадлежности опытных данных
рассматриваемому закону не отвергается;

 - гипотеза отвергается;
- гипотеза отвергается;
где  ;
;
где  вычисляется по формуле
вычисляется по формуле
 ,
,
где  - экспериментальные частоты попадания исходных данных в интервал;
- экспериментальные частоты попадания исходных данных в интервал;
 - теоретические частоты по уравнению плотности распределения;
- теоретические частоты по уравнению плотности распределения;
к – число степеней свободы, равное к = К-Н;
К – число интервалов гистограммы;
Н – число наложенных связей, равное Н=П+1;
П=4 – число параметров закона распределения.
Н=4+1=5; к=6 – 5=1.
Вероятность попадания эмпирических данных в j-и интервал определяется по формуле

Теоретическая частота попадания в интервал определяется по формуле
 .
.
Результаты подсчета  записаны в таблице 3
записаны в таблице 3
 Таблица 3 – Поэтапное вычисление
Таблица 3 – Поэтапное вычисление 
| № интервала | 
| 
| 
| 
| 
| 
| 
|
| 0,000011 | 0,07 | 4,2 | 6,8 | 46,24 | |||
| 0,000019 | 0,13 | 7,8 | 0,2 | 0,04 | 0,01 | ||
| 0,000028 | 0,19 | 11,4 | -5,4 | 29,16 | 2,6 | ||
| 0,000030 | 0,20 | ||||||
| 0,000024 | 0,16 | 9,6 | 3,4 | 11,56 | 1,2 | ||
| 0,000013 | 0,09 | 5,4 | 4,6 | 21,16 | 3,9 |

По таблице 1 приложения В определяется значение вероятности критерия Пирсона
 - гипотеза отвергается.
- гипотеза отвергается.
4.2 Проверка гипотезы по критерию Романовского
Критерий Романовского записывается в виде следующего альтернативного условия, отвечающего правосторонней критической области
 - гипотеза о принадлежности опытных данных к рассматриваемому закону не отвергается;
- гипотеза о принадлежности опытных данных к рассматриваемому закону не отвергается;
 - гипотеза отвергается;
- гипотеза отвергается;
где к - число степеней свободы.
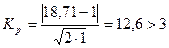 - гипотеза отвергается.
- гипотеза отвергается.
4.3 Проверка гипотезы по критерию Колмогорова
Критерий Колмогорова записывается в виде следующего альтернативного условия, отвечающего левосторонней критической области
 - гипотеза о принадлежности опытных данных к рассматриваемому закону не отвергается;
- гипотеза о принадлежности опытных данных к рассматриваемому закону не отвергается;
 - гипотеза отвергается;
- гипотеза отвергается;
где  - эмпирическая функция распределения, определяющееся по формуле
- эмпирическая функция распределения, определяющееся по формуле  ,
,
 - теоретическая функция распределения,
- теоретическая функция распределения,
n – объем выборки.
Таблица 3 – Результаты подсчета для определения критерия Колмагорова
| № интервала | 
| 
|  - - 
|
| 0,18 | 0,08 | 0,1 | |
| 0,31 | 0,19 | 0,12 | |
| 0,41 | 0,36 | 0,05 | |
| 0,61 | 0,58 | 0,03 | |
| 0,83 | 0,78 | 0,05 | |
| 0,92 | 0,08 |


 - гипотеза отвергается.
- гипотеза отвергается.
 График эмпирической и теоретической функции распределения
График эмпирической и теоретической функции распределения
 t
t






