Одним із завдань вимірювального експерименту є виявлення систематичних похибок, важливість якого полягає в тому, що така невиявлена похибка більш небезпечна, ніж випадкова, бо вона постійно спотворює результат вимірювання.
Для кожного різновиду систематичних похибок існують свої методи зменшення їх впливу, однак існують загальні методи, які можна застосовувати для корекції систематичних похибок різного походження. Розглянемо деякі з цих методів.
Зменшення впливу систематичних (інструментальних) похибок внесенням поправок до показів приладу.
Усунути систематичні похибки можна введенням поправок  , які чисельно дорівнюють значенню абсолютної систематичної похибки
, які чисельно дорівнюють значенню абсолютної систематичної похибки 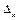 , але протилежні за знаком:
, але протилежні за знаком:
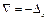 .
.
Отже, поправка – це значення величини, що алгебраїчно додається до результату вимірювання для вилучення систематичної похибки.
Інструментальну систематичну похибку можна виявити перевіркою робочого засобу вимірювань за допомогою зразкового, що має вищу точність. Вимірювальні прилади періодично перевіряють (повіряють), при цьому основною метрологічною операцією є експериментальне оцінювання фактичних значень похибок в певних місцях шкали приладу. Результатом метрологічної перевірки (повірки) є оцінки значень систематичних похибок на зазначених відмітках. Записані в таблицю з протилежним знаком експериментальні похибки утворюють таблицю поправок. Ці поправки можна враховувати при виконанні вимірювань для коригування систематичних похибок. Поправлений (скоригований) результат вимірювання отримують додаванням поправки  до показу:
до показу:  .
.
 Аналітичний розрахунок поправок (методична систематична похибка). У певних випадках систематичну похибку можна оцінити і, відповідно, поправити результат на основі аналізу вимірювальної схеми з використанням інформації про характеристики елементів схеми.
Аналітичний розрахунок поправок (методична систематична похибка). У певних випадках систематичну похибку можна оцінити і, відповідно, поправити результат на основі аналізу вимірювальної схеми з використанням інформації про характеристики елементів схеми.
Таким способом можна оцінювати і коригувати систематичні похибки, наприклад, від взаємодії ЗВТ з об’єктом вимірювання. Зокрема, при вимірюванні струму (рис. 5.5), внаслідок вмикання в коло амперметра з ненульовим опором 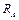 , опір кола збільшується, тому струм зменшується, тобто виникає методична похибка від взаємодії. За відомих опорів кола
, опір кола збільшується, тому струм зменшується, тобто виникає методична похибка від взаємодії. За відомих опорів кола  та амперметра
та амперметра 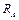 цю похибку можна оцінити відповідно до виразу
цю похибку можна оцінити відповідно до виразу 
і далі внести поправку у результат вимірювання. Насправді зазначені опори відомі не точно, тому повністю виключити методичну похибку розрахунковим шляхом не вдається, ця похибка лише зменшується.
Зменшення систематичних похибок приладу методом заміщення.
 Суть методу заміщення полягає у тому, що виконують два вимірювання (рис. 5.17).
Суть методу заміщення полягає у тому, що виконують два вимірювання (рис. 5.17).
Перше вимірювання - до входу приладу подають вимірювану величину X і отримують показ х, що містить систематичну похибку  :
:  .
.
Друге - до входу приладу під’єднують вихід міри Хм, регулюючи яку, добиваються попереднього показу приладу:  .
.
Прирівнюючи обидва результати, отримаємо значення вимірюваної величини  , що теоретично дорівнює показу міри, а похибка вимірювання визначається похибкою міри
, що теоретично дорівнює показу міри, а похибка вимірювання визначається похибкою міри  і становить:
і становить:  .
.
Виключення систематичних похибок способом заміщення можна проілюструвати на прикладі вимірювання опору, ємності чи індуктивності мостовим методом змінного струму, коли після зрівноваження кола моста об’єкт вимірювання заміщують відповідно магазином опору, ємності або індуктивності і підбирають значення заміщуючої величини так, щоб відновити рівновагу моста при попередніх значеннях його інших плеч. Завдяки цьому виключаються похибки, спричинені недосконалістю підгонки значень опорів плечей моста, впливом опору ізоляції та ін.
Спосіб заміщення вважається одним з найбільш надійних способів виключення систематичних похибок довільного походження.
Метод протиставлення полягає в тому, що вимірювана величина двічі порівнюється з величиною, яка відтворюється мірою, причому перед другим порівнянням вони взаємно міняються місцями у вимірювальному колі. Такий метод застосовують при вимірюваннях з приладами зрівноважування, в яких є можливість переставити місцями вимірювану величину і регульовану міру. Наприклад, при зважуванні на терезах або при вимірюванні опору мостовим методом. Розглянемо останній приклад (рис. 5.18). Нехай при вимірюванні опору міст зрівноважили і отримали значення опору плеча порівняння  , тобто
, тобто  ,
,
 де
де  - опори плеч відношень моста, похибки яких треба скоригувати. Для цього в другому вимірюванні переставимо місцями вимірюваний опір і опір плеча порівняння й знову зрівноважимо міст, звичайно при дещо іншому опорі плеча порівняння
- опори плеч відношень моста, похибки яких треба скоригувати. Для цього в другому вимірюванні переставимо місцями вимірюваний опір і опір плеча порівняння й знову зрівноважимо міст, звичайно при дещо іншому опорі плеча порівняння  , тобто
, тобто  .
.
Розділивши одне рівняння на друге, отримаємо 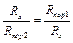 , звідки значення вимірюваного опору
, звідки значення вимірюваного опору  , яке теоретично не залежить від опорів плеч відношення, тобто і їх похибок.
, яке теоретично не залежить від опорів плеч відношення, тобто і їх похибок.
Залишкова відносна похибка 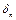 результату вимірювання при застосуванні методу протиставлення визначається похибкою
результату вимірювання при застосуванні методу протиставлення визначається похибкою  регульованої міри - плеча порівняння:
регульованої міри - плеча порівняння:  .
.
Метод симетричних в часі спостережень (зменшення прогресуючих похибок). Нагадаємо, що прогресуючою називають похибку, що в часі змінюється лінійно (наростає чи спадає). Оскільки загалом лінія описується двома параметрами: початковим значенням  та крутизною
та крутизною  , то похибка в часі
, то похибка в часі

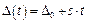 .
.
При невідомому значенні вимірюваної величини для корекції прогресуючої похибки треба виконати принаймні три вимірювання.
Серед різних варіантів найпростішим є так званий метод симетричних спостережень, в якому через рівні інтервали часу  виконують три вимірювання (рис. 5.19):
виконують три вимірювання (рис. 5.19):
- в момент часу 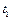 вимірюють відоме значення Хм вихідної величини міри і отримують показ
вимірюють відоме значення Хм вихідної величини міри і отримують показ  ;
;
- в момент часу  вимірюють значення X вимірюваної величини і отримують показ
вимірюють значення X вимірюваної величини і отримують показ  ;
;
- в момент часу  знову вимірюють це ж саме відоме значення Хм вихідної величини міри і отримують показ
знову вимірюють це ж саме відоме значення Хм вихідної величини міри і отримують показ
 .
.
Обчисливши середнє значення першого і третього результату
 ,
,
знаходять значення прогресуючої похибки в момент часу  , яке підставляють у друге рівняння і знаходять значення вимірюваної величини:
, яке підставляють у друге рівняння і знаходять значення вимірюваної величини:  .
.
Залишкова похибка методу симетричних спостережень визначається похибкою міри:
 .
.
Спосіб компенсації похибки за знаком полягає в тому, що дану величину вимірюють двічі, але умови вимірювання змінюють так, щоб стала систематична похибка, яка підлягає виключенню (відома по походженню, але не відома за значенням), входила в результати вимірювань з протилежними знаками. Тоді середнє арифметичне результатів стає вільним від цієї похибки.
Наприклад, результат першого вимірювання:  , а другого –
, а другого –  ,
,
де  – систематична складова похибки, що підлягає виключенню;
– систематична складова похибки, що підлягає виключенню;  – вимірювальна величина.
– вимірювальна величина.
На основі цих виразів середнє арифметичне обох результатів: 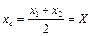 ; звідки видно, що складова Δ виключена з результату
; звідки видно, що складова Δ виключена з результату  .
.
Спосіб компенсації похибки може бути використаний для виключення похибок, джерела яких мають направлену дію. Цей метод часто використовують при вимірюванні екстремальних значень (максимума і нуля) невідомої фізичної величини.
Спосіб компенсації похибки за знаком застосовується, наприклад, для виключення похибки, спричиненої впливом паразитних термо- е. р. с. у вимірювальних колах постійного струму. В цьому випадку друге вимірювання виконують при протилежному напрямку струму у вимірювальному колі, щоб змінився вплив знаку термо- е. р. с. Для виключення впливу магнітного поля Землі на покази електровимірювального приладу останній перед другим вимірюванням повертають на 180° у горизонтальній площині.
Навіть після виключення інструментальних та методичних похибок у результатах вимірювань знаходять залишки систематичних похибок (так звані невиключені залишки систематичних похибок); виявити їх можна на основі аналізу умов проведення експерименту. Треба визначити, в яких межах  відносно результату вимірювання з певною ймовірністю Р можна очікувати знаходження істинного значення Х вимірюваної величини залежно від невиключених залишків систематичної похибки.
відносно результату вимірювання з певною ймовірністю Р можна очікувати знаходження істинного значення Х вимірюваної величини залежно від невиключених залишків систематичної похибки.
Інструментальна похибка, що залежить від неточності аналогового вимірювального приладу, обчислюється за формулою, яку виведено з формули:
 - надійна межа невиключених залишків систематичних похибо к.
- надійна межа невиключених залишків систематичних похибо к.
Підсумовування систематичних похибок.
У переважній більшості практичних вимірювальних задач похибка вимірювання може бути описана як алгебрична сума декількох складових (наприклад, основних і додаткових похибок ЗВТ, методичних, особистих тощо), кожна з яких впливає на сумарну через певний коефіцієнт впливу  :
:  .
.
Якщо похибка вимірювання містить велику кількість складових, то мало ймовірно, щоб усі вони одночасно прийняли своє найбільше (граничне) значення та ще й всі з погодженими знаками. Тому для підсумовування великої кількості систематичних похибок використовують квазістатистичний підхід, який дає більш реалістичну оцінку похибки, якою є довірча похибка.
 ,
,
де К(Рдов,п) - коефіцієнт, що залежить від довірчої ймовірності Рдов, розподілу складових і їх кількості п (
 ;
; 
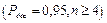 ;
; 
 ).
).






