В залежності від виду цільової функції і обмежень математичне програмування поділяється на лінійне і нелінійне. У задачах лінійного програмування можливі випадки, коли параметри управління набувають лише цілі дискретні значення. При розв’язанні подібних задач використовують цілочислове програмування. Коли вихідні параметри змінюються у певних межах, тоді використовують параметричне програмування.
На теперішній час не існує загальних і досить ефективних методів розв’язання задач нелінійного програмування. Лише для певного класу нелінійних задач, система обмежень яких лінійна, а цільова функція нелінійна, але має властивість опуклості, розроблені досить ефективні методи, що одержали назву методів опуклого програмування. На практиці доволі часто виникають ситуації, в яких необхідно приймати рішення при наявності двох або більше сторін, що мають різну мету. Результати будь-якої дії кожної із сторін залежать від рішень партнерів. Для розв’язання задач з конфліктними ситуаціями використовують математичні методи теорії ігор.
Динамічне програмування – один з розділів методів оптимізації, в яких процес прийняття рішення може бути розбитий на окремі етапи. В основі методу лежить принцип оптимальності, який розробив Р. Беллман.
Теорія масового обслуговування вивчає системи, контролює їх характеристики для здійснення оптимізації системи в цілому.
Вище перелічено основні розділи математичного програмування, які плануються вивчати протягом семестру.
Лінійне програмування – наука про методи дослідження і знаходження екстремальних (найбільших і найменших) значень лінійної функції, на невідомі якої накладаються лінійні обмеження.
Ця лінійна функція називається цільовою, а обмеження які математично записуються у вигляді рівнянь або нерівностей називаються системою обмежень.
Математичне вираження цільової функції та її обмежень називається математичною моделлю економічної задачі або економіко-математичною моделлю.
У загальному вигляді математична модель задачі лінійного програмування можна записати

при обмеженнях

де  - невідомі,
- невідомі,  - задані сталі величини.
- задані сталі величини.
Всі або декілька рівнянь системи обмежень можуть бути записані у вигляді нерівностей.
Математична модель у більш скороченому вигляді може бути записана

з обмеженнями
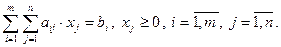
Деякі задачі лінійного програмування вимагають цілочислового розв’язку. До них відносяться задачі з виробництва і розподілу не діленої продукції (випуск верстатів, телевізорів, автомобілів тощо). У загальному вигляді математична модель задачі цілочислового програмування має вигляд

з обмеженнями
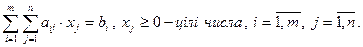
Математична модель задачі нелінійного програмування у загальному вигляді формулюється наступним чином: знайти вектор  , що задовольняє системі обмежень
, що задовольняє системі обмежень

і має екстремум цільової функції
 ,
,
де  - змінні,
- змінні, 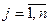 ;
;  - задані функції від п змінних,
- задані функції від п змінних,  - фіксовані значення (вільні члени).
- фіксовані значення (вільні члени).
Нелінійне програмування використовується при прогнозуванні промислового виробництва, управлінні товарними ресурсами, плануванні обслуговування і ремонту обладнання тощо.
Дробово-лінійне програмування відноситься до методів лінійного програмування, тому що має цільову функцію, записану у нелінійному вигляді. Задача дробово-лінійного програмування у загальному вигляді записується наступним чином

при обмеженнях
 ,
,
де  постійні коефіцієнти і
постійні коефіцієнти і  .
.
Динамічне програмування – один із розділів оптимального програмування, у якому процес прийняття рішення і управління може бути розбитий на окремі етапи (кроки).
Економічний процес є керованим, якщо можна впливати на хід його розвитку. Під управлінням розуміють сукупність рішень, які приймаються на кожному етапі для впливу на розвиток процесу.
Наприклад: випуск продукції є керованим процесом, тому що за управління можна прийняти сукупність рішень (початок року, кварталу, місяця) з забезпечення підприємства сировиною, заміні обладнання, фінансуванню тощо. Необхідно організувати випуск продукції таким чином, щоб прийняті рішення на окремих етапах сприяли одержанню максимально можливого обсягу продукції або прибутку.
Динамічне програмування дозволяє звести одну складну задачу із багатьма змінними до багатьох задач з малою кількістю змінних. Це значно скорочує обсяг обчислень і прискорює процес прийняття управлінського рішення.
На відміну від лінійного програмування, у якому симплексний метод є універсальним методом розв’язку, у динамічному програмуванні такого універсального методу не існує.
Одним із основних методів динамічного програмування є метод рекурентних співвідношень, який ґрунтується на основі принципу оптимальності, який розроблений американським вченим Р. Беллманом. Принцип полягає у тому, що яким би не були початковий стан на будь-якому етапі і управління, яке обрано на цьому етапі, наступні управління повинні обиратися оптимальними відносно стану, до якого прийде система у кінці даного етапу. Використання даного принципу гарантує, що управління, обране на будь-якому етапі, не локально краще, а краще з точки зору процесу в цілому.
У деяких задачах динамічного програмування процес управління розбивається на кроки. При розбитті на декілька кроків ресурсів діяльності підприємства, кроком доцільно вважати часовий проміжок, а при розподілі коштів між підприємствами – номер наступного підприємства. У інших задачах розбиття на кроки вводиться штучно. Наприклад, неперервний керований процес можна розглядати як дискретний, штучно розбивши його на часові відрізки (етапи). Виходячи з умови задачі, у кожному конкретному випадку довжину кроку обирають таким чином, щоб на кожному етапі одержати просту задачу оптимізації і забезпечити необхідну точність обчислень.
Види наукових публікацій.
Результати наукових досліджень оприлюднюють у вигляді різних публікацій. Це сприяє встановленню пріоритету автора (дата підписання публікації до друку – це дата пріоритету науковця), а також свідчить про особистий внесок дослідника у розробку наукової проблеми (особливе значення мають індивідуальні публікації, роботи у співавторстві потребують додаткових роз’яснень).
Публікації відображають основний зміст, новизну наукового дослідження і фіксують завершення певного етапу дослідження або роботи в цілому. Крім цього, публікації забезпечують первинною науковою інформацією суспільство, сповіщають наукове співтовариство про появу нового наукового знання і передають індивідуальний результат у загальне надбання.
Існують такі види наукових публікацій: монографія, стаття, автореферат, препринт, тези доповідей, наукова доповідь, збірник наукових праць. Наукові публікації виходять друком у формі друкованих або електронних видань.
Видання – це такий документ, що пройшов редакційно-видавниче опрацювання, виготовлений друком, тисненням або іншим способом, містить інформацію, призначену для поширення і відповідає вимогам державних стандартів, інших нормативних документів щодо видавничого оформлення і поліграфічного виконання.
Монографія – науково-книжкове видання певного дослідження однієї проблеми або теми, що належить одному або кільком авторів.
Стаття – це вміщені в науковому журналі чи збірнику результати дослідження конкретного питання, що мають певне наукове й практичне значення.
Автореферат дисертації – це наукове видання у вигляді брошури авторського реферату проведеного дослідження, яке подається на здобуття наукового ступеня.
Препринт – наукове видання з матеріалами попереднього характеру, які публікуються до виходу у світ видання, у якому вони мають бути розміщені.
Тези доповідей, матеріали наукової конференції – це неперіодичні збірники підсумків наукових конференцій, доповідей, рекомендацій та рішень.
Збірники наукових праць – це збірники матеріалів досліджень, які виконано у наукових установах, навчальних закладах та наукових товариствах.






