ОСНОВНЫЕ ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Основные определения и термины
Возникновение отказов в информационных системах зависит от разных факторов и носит случайный характер. Поэтому для количественной оценки различных характеристик систем используются вероятностные методы.
В теории вероятностей случайной называется величина, которая в результате опыта может принять то или иное значение, предугадать которое заранее и достоверно невозможно.
Событием в теории вероятностей считается всякий факт, который в результате опыта может произойти, а может и не произойти.
Для количественного сравнения между собой событий по степени их возможности используется определенное число, которое тем больше, чем более возможно событие. Такое число называется вероятностью события.
В практике о вероятности события судят по частоте его появления. Если
в n опытах событие А появилось m раз, то его частота или статистическая вероятность может быть определена соотношением
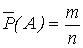 .
.
Невозможным называется событие, которое заведомо не произойдет. Вероятность невозможного события равна нулю.
Достоверным называется событие, которое обязательно произойдет. Вероятность достоверного события равна единице.
Вероятность произвольного случайного события изменяется от нуля до единицы.
Если случайное событие имеет очень малую вероятность, то практически можно считать, что в единичном опыте это событие не наступит. Очень малая вероятность – это значения, заключенные между 0,01 и 0,05. Это свойство называется принципом практической невозможности маловероятных событий.
При неограниченном увеличении числа опытов статистическая вероятность сходится по вероятности к математической, т. е. частота с вероятностью сколь угодно близкой к единице, приближается к математической вероятности Р(А).
Если исходы (результаты) испытаний единственно возможны и равновозможны, математическая вероятность события А может быть вычислена по формуле:
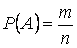 ,
,
где n – общее число равновозможных элементарных исходов испытаний;
m – число благоприятных исходов, в которых появляется событие А.
При вычислении величин m и n используется теория сочетаний.
Число сочетаний из m элементов по n вычисляется по любой из двух формул:
 , (2.1)
, (2.1)
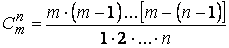 . (2.2)
. (2.2)
Примеры:
 ;
;  ;
; 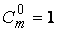 .
.
Гипергеометрическое распределение
При решении задач контроля качества продукции используется гипергеометрическое распределение
 . (2.3)
. (2.3)
Из группы в n элементов, состоящих из m элементов одного типа и (n – m) элементов другого типа, берется наугад группа из r элементов. Определяется вероятность того, что среди r элементов будет k элементов первого типа.






