Второй признак сравнения
Теорема (о втором признаке сравнения)
Если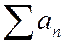 
и 
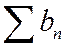- ряды с положительными членами и существует конечный, не равный нулю предел отношения их общих членов при п ®¥:
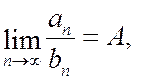
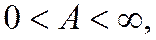(1.30)
то эти ряды сходятся или расходятся одновременно.
Пример. Исследовать сходимость ряда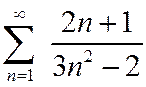 
.
При достаточно больших значениях n имеем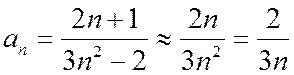 
. Поэтому в качестве ряда сравнения можно рассмотреть гармонический ряд с общим членом 
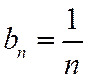Тогда
.
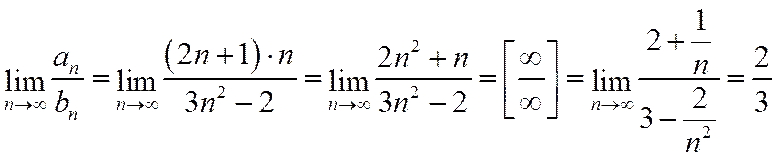На основании предельного признака сравнения заключаем; что в силу расходимости гармонического ряда расходится и данный ряд с общим членом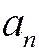 
.
Признак Д’Аламбера
Теорема (признак Д'Аламбера). Если для знакоположительного ряда
(
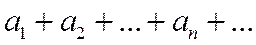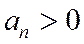) (1.31)
существует предел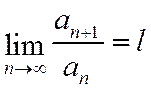 
, (1.32)
то:
при l < 1 ряд сходится,
при l > 1 ряд расходится;
при l =1 ряд может оказаться как сходящимся, так и расходящимся, т.е. признак неприменим.
Пример 1. Исследовать на сходимость ряд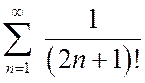 
.
.
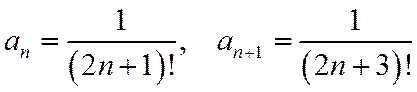Последующий член ряда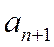 
получается из предыдущего 
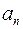заменой n на n +1.
= 
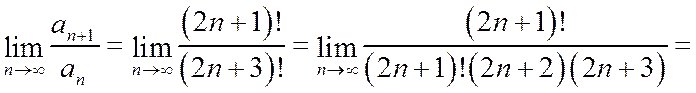
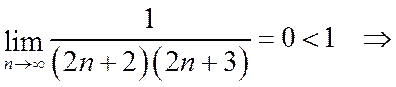ряд сходится.
Пример 2.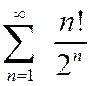 
.
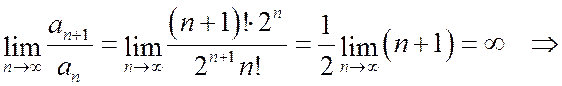ряд расходится (заметим, что в формулировке теоремы не требуется, чтобы предел был конечным).
Пример 3.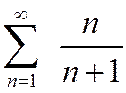 
.
.
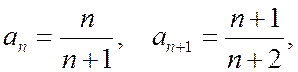
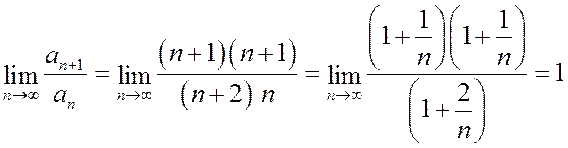Здесь признак Даламбера не работает. Однако общий член ряда не стремится к нулю:
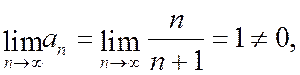
т.е. выполняется достаточный признак расходимости ряда. Ряд расходится.
Замечание. Признак Даламбера удобно применять, когда общий член ряда содержит факториалы или показательные функции относительно п.
Радикальный признак Коши
Рассмотрим ряд с неотрицательными членами
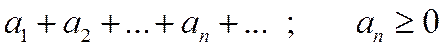. (1.37)
Теорема (радикальный признак Коши)
Если для ряда (1.39) c неотрицательными членами существует конечный предел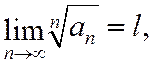 
то:
при l < 1 ряд сходится,
при l > 1 ряд расходится;
при l =1 ряд может оказаться как сходящимся, так и расходящимся, т.е. признак неприменим.
Доказательство аналогично доказательству теоремы Д'Аламбера.
Замечание. Радикальный признак Коши эффективен, если общий член ряда имеет вид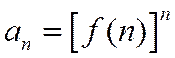 
, т.е. является какой-либо функцией от номера п, возведенной в степень п.
Пример. Исследовать сходимость ряда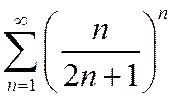 
.
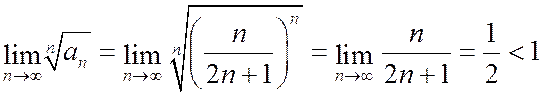
- ряд сходится.
Интегральный признак Коши
Теорема (интегральный признак Коши).
Пусть дан ряд
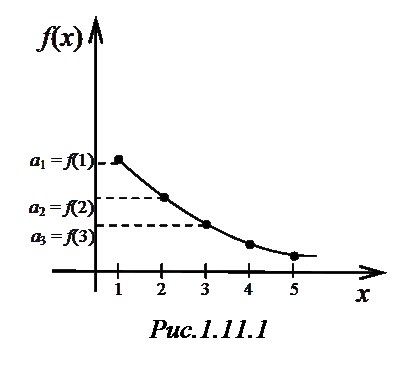
(1.38)
с положительными и монотонно убывающими членами, т.е.
, 
.
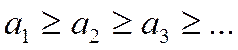Пусть члены этого ряда являются значениями некоторой положительной, непрерывной и убывающей на полуинтервале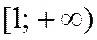 
функции 
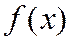при натуральных значениях аргумента:
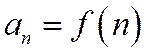
Тогда если сходится несобственный интеграл:
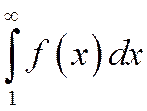, (1.39)
то сходится и ряд (1.38)(См. рис.1.11.1).
Пример 1.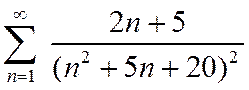 
.
В качестве функции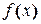 
возьмем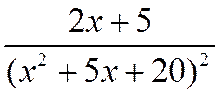 
Это легко сделать, заменив п на х. Тогда
.
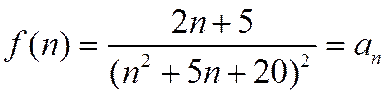Составим несобственный интеграл:
,
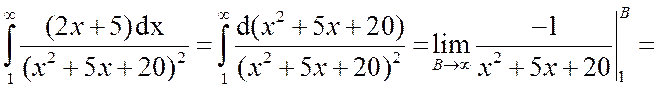
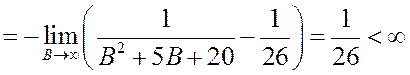следовательно, ряд сходится.
Пример 2. Исследовать на сходимость гармонический ряд:
.
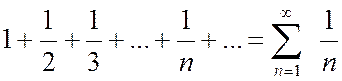1) Исследуем на сходимость по признаку Даламбера: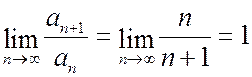 
,
т.е. о сходимости ряда по признаку Даламбера ничего сказать нельзя.
2) Применим более сильный признак сходимости - интегральный признак Коши. В качестве функции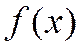 
возьмем 
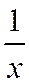, тогда 
.
,
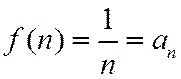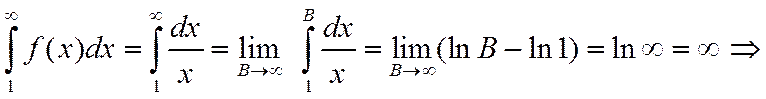гармонический ряд расходится.
Замечание. Иногда приходится брать интеграл не от 1, а от других чисел, например, от 2.
Обобщённый гармонический ряд
Определение. Ряд вида:
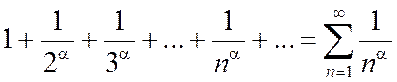, (1.46)
где a - положительное число, называют обобщённым гармоническим.
Если a=1, то имеем гармонический ряд, который расходится.
Применим интегральный признак Коши, приняв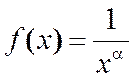 
.
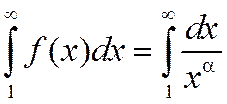. (1.47)
Во втором семестре I курса мы выяснили, что этот несобственный интеграл сходится при a >1 и расходится при a £1. Согласно теореме об интегральном признаке Коши обобщённый гармонический ряд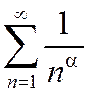 
ведёт себя так же: сходится при 
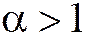и расходится при 
.
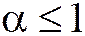Пример.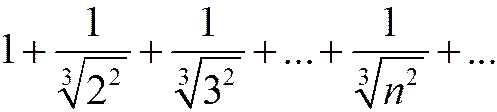 
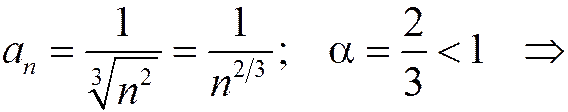ряд расходится.
