ЛАБОРАТОРНАЯ РАБОТА № 1.5
«ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТВЕРДЫХ ТЕЛ
МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ»
I.Цель работы: ознакомление с экспериментальным методом определения моментов инерции тел с помощью упругих крутильных колебаний.
II.Описание установки
Общий вид крутильного маятника представлен на рисунке. Между основанием 1 и верхним держателем 2 находится рабочая часть прибора. Она состоит из рамки 4, в которой закрепляется исследуемое тело 5, и стальной проволоки 3, на которой подвешена рамка. Система измерения числа и времени колебаний включает фотоэлектрический датчик 6 и миллисекундомер 7. При двукратном пересечении светового индикатора колеблющейся рамкой датчик вырабатывает сигнал числа колебаний. Синхронно работающий миллисекундомер определяет время заданного числа колебаний.
III.Методика измерений и расчетные формулы
В случае крутильных колебании при повороте рамки с исследуемым телом на некоторый угол φ вокруг оси, совпадающей с проволокой, проволока закручивается и в ней возникают упругие силы, которые стремятся возвратить рамку в положение равновесия. Под действием этих сил рамка с телом будет совершать крутильные колебания в горизонтальной плоскости. Вращающий момент М упругих сил пропорционален углу закручивания:
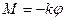, (1)
где k - коэффициент упругости проволоки, равный моменту сил, необходимых для закручивания ее на единичный угол.
Применяя основной закон динамики вращательного движения (при незначительном трении), имеем:
, (2)
где J - момент инерции тела.
Решение уравнения (2) будет иметь вид:
, (3)
где φ - циклическая частота колебаний.
Продифференцировав выражение (3) дважды по времени и подставив его в выражение (2), найдем период упругих крутильных колебаний:
. (4)
Для экспериментального определения момента инерции J колеблющегося тела на основе соотношения (4) требуется знать период колебании T и коэффициент упругости k проволоки. Период колебаний определяется на основе измерения времени t определенного числа n колебании:
. (5)
Для нахождения величины k определяется период крутильных колебаний одного из предложенных параллелепипедов вокруг оси, перпендикулярной основанию. Из определения момента инерции следует, что величина J для данного опыта равняется
(6)
где m - масса параллелепипеда; a и b - длины сторон основания, перпендикулярного оси вращения. Подставляя экспериментальный T и расчетный J в соотношение (4), определяют значение параметра k.
Окончательно моменты инерции предложенных тел относительно произвольных осей вращения можно найти по формуле, вытекающей из (4):
. (7)
