Как уже было отмечено выше, стеганографические методы скрытия данных в пространственной области изображения являются нестойкими к большинству из известных видов искажений. Так, например, использование операции компрессии с потерями (относительно изображения, это может быть JPEG-компрессия) приводит к частичному или, что более вероятно, полному уничтожению встроенной в контейнер информации. Более стойкими к разнообразным искажениям, в том числе и компрессии, являются методы, использующие для скрытия данных не пространственную область контейнера, а частотную.
Существует несколько способов представления изображения в частотной области. При этом используется та или иная декомпозиция изображения, используемого в качестве контейнера. Например, существуют методы на основе использования дискретного косинусного преобразования (ДКП), дискретного преобразования Фурье (ДПФ), вейвлет-преобразования, преобразования Карунена-Лоева и некоторые другие. Подобные преобразования могут применяться либо к отдельным частям изображения, либо к изображению в целом.
Наибольшее распространение среди всех ортогональных преобразований в стеганографии получили вейвлет-преобразования и ДКП [5], что определенной мерой объясняется значительным распространением их использования при компрессии изображений. Кроме того, для скрытия данных целесообразно применять именно то преобразование изображения, которому последнее будет подвергаться со временем при возможной компрессии. Например, известно, что алгоритм ДКП является базовым в стандарте JPEG, а вейвлет-преобразования — в стандарте JPEG2000.
Стеганоалгоритм может быть достаточно стойким к последующей компрессии изображения, только если он будет учитывать особенности алгоритма перспективного сжатия. При этом, конечно, стеганоалгоритм, в основу которого заложено вейвлет-преобразование, совсем не обязательно будет стойким к дискретнокосинусному алгоритму сжатия, и наоборот. Авторы [5] отмечают, что еще большие трудности возникают при выборе метода стеганопреобразования во время скрытия данных в потоковом видео. Причина этого — одной из составляющих алгоритмов компрессии видеоинформации (в дополнение к компрессии неподвижного кадра), является кодирование векторов компенсации движения. При компрессии неподвижного изображения данная компенсация отсутствует за ненадобностью. Чтобы быть в достаточной степени стойким, стеганоалгоритм должен учитывать данный фактор.
Остается также открытым вопрос о существовании стойкого стеганопреобразования, которое было бы независимым от применяемого в дальнейшем алгоритма компрессии. Рассмотрение различных ортонормированных преобразований, таких как ДПФ, ДКП, преобразование Хартли, субполосное преобразование и др. с позиции теории информации проведено авторами [19,44].
На сегодняшний день известно достаточно большое количество моделей, позволяющих оценить пропускную способность канала передачи скрытых данных. Ниже приведена одна из них, представленная в работах [S, 84].
Пусть С — первичное изображение (контейнер-оригинал), М — сообщение, которое подлежит скрытию. Тогда модифицированное изображение (стеганоконтейнер) S = C+M. Также предполагается, что модифицированное изображение S визуально неотличимо от первичного и может быть подвергнуто в стеганоканале компрессии с потерями:  , где
, где  — оператор компрессии.
— оператор компрессии.
Задача адресата — извлечь из полученного контейнера  встроенные на предыдущем этапе биты данных Мi,
встроенные на предыдущем этапе биты данных Мi,
Основное, что будет при этом интересовать нас, — ответ на вопрос: какое количество бит можно эффективно встраивать в изображение и со временем извлечь из него при условии удовлетворительно низкой вероятности ошибок на последнем этапе. Другими словами, какова пропускная способность канала передачи скрытых данных при условии наличия в канале связи определенного алгоритма компрессии? Блок-схема такого стеганоканала представлена на рис: 5.23.

Рис. 5.23. Блок-схема стеганоканал с атакой в виде компрессии
Сообщение М передается по каналу, который имеет, два источника "шума": С — изображение-контейнер и "шум"  , возникающий в результате операций компрессии/декомпрессии. При этом
, возникающий в результате операций компрессии/декомпрессии. При этом  и М* — возможно искаженные стеганоконтейнер и, как результат, — оценка полезного сообщения.
и М* — возможно искаженные стеганоконтейнер и, как результат, — оценка полезного сообщения.
Структурная схема стеганосистемы приведена на рис. 5.24.

Рис. 5.24. Структурная схема стеганосистемы при наличии в стеганоканале атаки компрессии
Изображение С раскладывается на D субполос (прямое преобразование), в каждую из которых встраивается скрываемая информация М. После обратного преобразования получается модифицированное изображение S. После компрессии/ декомпрессии  в канале связи получается изображение
в канале связи получается изображение  , которое на принимающей стороне вновь подвергается прямому преобразованию и из каждой субполосы D независимо извлекается скрытоехообщение— оценка М*.
, которое на принимающей стороне вновь подвергается прямому преобразованию и из каждой субполосы D независимо извлекается скрытоехообщение— оценка М*.

Рис. 5.25. Зависимость шума изображения (сплошная линия) и шум» обработки (пунктирная линия) от частоты
Как указывается в [5], реальные изображения не представляют собой случайные процессы с равномерно распределенными значениями величин. Известно, и данный факт используется в алгоритмах компрессии, что большая часть энергии изображений сосредоточена в низкочастотной (НЧ) области спектра. Отсюда и возникает необходимость в осуществлении декомпозиции изображения на субполосы, к которым прибавляется стеганособщение. НЧ субполосы содержат основную часть энергии изображения и, таким образом, носят шумовой характер. Высокочастотные (ВЧ) субполосы спектра Изображения наибольшим образом поддаются влиянию со стороны разнообразных алгоритмов обработки, таких как, например, компрессия или НЧ-фильтрация. Таким образом, можно сделать вывод, что для встраивания сообщения самыми оптимальными являются среднечастотные (СЧ) субполосы спектра изображения. Типичное распределение шума изображения и шума-обработки по спектру частоты изображено на рис. 5.25 [44, 85].
Стеганографический канал можно разложить на ряд независимых подканалов. Такое разложение совершается за счет выполнения прямого и обратного преобразований. В каждом из D подканалов существует по два источника шума. Пусть  , при j=1,..., D — дисперсия коэффициентов преобразования (шум изображения) в каждом из подканалов. Тогда выражение для пропускной способности канала стеганосистемы приобретет вид:
, при j=1,..., D — дисперсия коэффициентов преобразования (шум изображения) в каждом из подканалов. Тогда выражение для пропускной способности канала стеганосистемы приобретет вид:
 (5.16)
(5.16)
где  —визуальный порог для_j-й субполосы
—визуальный порог для_j-й субполосы  — максимально допустимая энергия стеганосообщения, исходя из требований сохранения визуального качества изображения); X и Y— пиксельный размер изображения-контейнера.
— максимально допустимая энергия стеганосообщения, исходя из требований сохранения визуального качества изображения); X и Y— пиксельный размер изображения-контейнера.
Выбор значения визуального порога базируется на учете свойств ЗСЧ. Известно, что шум в ВЧ областях изображения более приемлемый, чем в НЧ областях.
Можно ввести некоторые весовые коэффициенты:  , где
, где 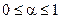 , a
, a  — константа.
— константа.
Случай, когда  , отвечает равномерному распределению стеганограммы по всем субполосам. Случай
, отвечает равномерному распределению стеганограммы по всем субполосам. Случай  отвечает распределению стеганограммы в соответствии с дисперсией субполос.
отвечает распределению стеганограммы в соответствии с дисперсией субполос.
После некоторых упрощений можно получить выражение для пропускной способности канала передачи скрытых данных:
 (5.17)
(5.17)
Знак приближения в выражении (5.17) является справедливым,  для любого значения. Очевидно, что при
для любого значения. Очевидно, что при  декомпозиция никоим образом не будет влиять на пропускную способность стеганоканала. При
декомпозиция никоим образом не будет влиять на пропускную способность стеганоканала. При  пропускная способность будет возрастать за счет того, что в области с низкой дисперсией (высокочастотной области) стеганосигналу прибавляется относительно больше энергии,
пропускная способность будет возрастать за счет того, что в области с низкой дисперсией (высокочастотной области) стеганосигналу прибавляется относительно больше энергии,
В [85] приведены результаты многочисленных экспериментов, которые позволили авторам дать определенные рекомендации относительно выбора вида преобразования для стеганографии. Известно, что преобразования можно упорядочить по достижимым выигрышам от алгоритма кодирования (рис. 5.26).

Рис. 5.26. Виды преобразований, упорядоченные по достижимым выигрышам от использования
Под выигрышем от кодирования подразумевается степень перераспределения дисперсий коэффициентов преобразования. Наибольший выигрыш дает преобразование Карунена-Лоева (ПКЛ), наименьший — разложение, за базисом единичного импульса (то есть отсутствие преобразования).
Преобразования, которые характеризуются высокими значениями выигрыша от кодирования, такие как ДКП, вейвлет-преобразования, характеризуются резко неравномерным распределением дисперсий коэффициентов субполос. Высокочастотные субполосы не подходят для встраивания из-за большого шума обработки, а низкочастотные — из-за высокого шума изображения (см. рис. 5.25), Поэтому, как отмечалось в [85], приходится ограничиваться среднечастотными полосами, у которых шум изображения приблизительно равен шуму обработки. Поскольку таких полос немного, то пропускная способность стеганоканала является сравнительно малой.
В случае применения преобразования с более низким выигрышем от кодирования, например, преобразования Адамара или Фурье, существует больше блоков, у которых шум изображения приблизительно равняется шуму обработки, а, следовательно, и пропускная способность выше. Вывод, к которому пришли авторы указанной работы, достаточно неожиданный: для повышения пропускной способности стеганографического канала целесообразно применять преобразования с меньшими выигрышами от кодирования, которые плохо подходят для компрессии сигналов.
Эффективность применения вейвлет-преобразования и ДКП для компрессии изображений объясняется тем, что они хорошо моделируют процесс обработки изображения в ЗСЧ, отделан существенные детали от второстепенных. Таким образом, данные преобразования более целесообразно использовать в случав присутствия активного нарушителя, поскольку модификация значимых, коэффициентов может привести к неприемлемому искажению изображения.
При применении преобразований с низкими значениями выигрыша от кодирования существует значительная опасность разрушения встроенных данных, по причине того, что коэффициенты преобразования менее стойки к модификациям. Однако при этом существует большая гибкость в выборе преобразования, и если последнее неизвестно нарушителю (хотя это и противоречит принципу Керхгофса) то модифицировать стеганограмму будет существенно сложнее.
Во время цифровой обработки изображения часто применяется двумерная версия дискретного косинусного преобразования:

 (5.18a)
(5.18a)
 (5.18б)
(5.18б)
где C(c, у) и S(x, у) — соответственно, элементы оригинального и восстановленного по коэффициентам ДКП изображения размерностью  ; х,у — пространственные координаты пикселей изображения;
; х,у — пространственные координаты пикселей изображения;  — массив коэффициентов ДКП;
— массив коэффициентов ДКП;  —координаты в частотной области;
—координаты в частотной области;  , если
, если  , и
, и  , если
, если  . Рассмотрим существующие методы, которые базируются на алгоритме ДКП.
. Рассмотрим существующие методы, которые базируются на алгоритме ДКП.






