В [3,15] представлено формальное теоретико-информационное определение устойчивости стеганосистемы относительно пассивных атак. Главная идея базируется на случайности избрания контейнера с из множества С с вероятностью Р с.
Встраивание в контейнер секретного сообщения можно описать как функцию, определенную на множестве С. Пусть Рс — вероятность формирования стеганосистемы Е (с, m, k) надмножестве S всех возможных стеганограмм, полученных с помощью стеганосистемы. Если контейнер с никогда не используется для получения стеганограмм, то РS(с) = 0. Для вычисления вероятности PS необходимо учитывать распределение вероятностей на множестве ключей К и множестве сообщений М.
Определим на множестве Q такое соотношение для относительной энтропии, с помощью которого можно измерить неэффективность принятия неверной гипотезы о распределении Р1 в случае истинного распределения P0.
(3.20)
где выражение 
является алгоритмическим отношением правдоподобия.
Относительная энтропия между двумя распределениями всегда неотрицательна и равна 0 только в случае тождественности данных распределений. Таким образом, для стеганопреобразования можно получить некоторую оценку.
Представим определение надежности стеганосистемы в терминах относительной энтропии.
Определение 3.1
Пусть 
— стеганографическая cистема; Ps — распределение вероятностей передачи каналом связи стеганограмм; Рс — распределение вероятностей передачи каналом связи пустых контейнеров. Система называется 
-надежной к пассивным атакам, если 
и является абсолютно надежной, если 
.
Как уже указывалось, соотношение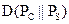 
равно нулю только в том случае, когда оба распределения вероятностей равны друг другу. Следовательно, стеганосистема является теоретически абсолютно надежной, если процесс встраивания секретного сообщения в контейнер не изменяет распределение РС. Абсолютно безопасная система может быть создана, например, на основании одноразовой гаммы [3].
На основании сказанного, формулируется следующая теорема.
Теорема 3.1
Существует абсолютно надежная стеганосистема
Доказательство
В [15] проведено конструктивное доказательство данного утверждения. Пусть контейнер С представляет собой равномерно распределенную n -битную последовательность для некоторого положительного n. Отправитель с помощью генератора ключа получает равномерно распределенный n -битный ключ К. Считается, что функция встраивания заключается в побитовом сложении по модулю 2 (операция XOR) n -битного секретного сообщения (в роли которого в данном случае выступает собственно контейнер С) с ключом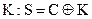 
. Получатель декодирует полученную последовательность повторным применением операции XOR: 
. Совершенно очевидно, что результирующая стеганограмма S также будет представлять собой распределенную n-битную последовательность. Следовательно, РС ~ PS, откуда 
. Теорема доказана.
