Стратифицированная выборка в любом случае оказывается точнее собственно-случайной. Этот метод особенно хорош, когда генеральная совокупность неоднородна. В этом случае собственно-случайный отбор крайне неэффективен (требует большого объема выборки).
Однако стратифицированная выборка может быть применена лишь при наличии дополнительной информации о генеральной совокупности (например, нам необходимо процентное соотношение мужчин и женщин, в случае, если мы хотим стратифицировать выборку по полу). Отсутствие такой информации делает применение стратифицированной выборки невозможным. Еще один недостаток стратифицированного отбора – это возможность систематической ошибки. Далее на примерах попытаемся проиллюстрировать различные способы применения стратифицированной выборки.
Пример: [6, 41]Возьмем опять данные о доходах из таблицы 1. Только теперь из этого же массива произведем не случайную, а стратифицированную выборку из четырех человек.
Для возможности проведения стратифицированной выборки сделаем допущение, что из предыдущей переписи мы знаем доходы респондентов за предыдущий период и имеем основания предполагать, что к этому периоду они не изменились или изменились пропорционально.
На основании этих данных можно стратифицировать генеральную совокупность по доходу. Результаты этого деления представлены в таблице 12.
Таблица 12.
Распределение респондентов по стратам.
| № группы. | Респонденты, попавшие в группу. |
| 1. | A,J,D. |
| 2. | L,G,F. |
| 3. | I,H,C. |
| 4. | E,K,B. |
Здесь в каждой группе (или страте) находятся люди с максимально близкими доходами. Необходимые нам четыре человека мы отбираем путем случайного отбора одного человека из каждой группы (т.е. проводим пропорциональную выборку).
В итоге мы получаем вполне репрезентативную по доходу выборку, т.к. в нашей выборке будут в нужной пропорции представлены люди с различным материальным достатком.
Более того, подобный отбор является надежнее случайного, т.к. при таком отборе не могут быть выбраны «плохие» выборки, т.е. выборки, содержащие только бедных или богатых (например, ADJL или BCEK). Однако стратифицированная выборка не всегда приносит выгоду, что показано в следующем примере.
Пример: [6, 42]Допустим, что перед нами опять встала необходимость провести стратифицированную выборку из респондентов, представленных в таблице 1. Далее предположим, что за период между переписью и опросом доходы респондентов претерпели значительные изменения, то выделенные нами группы на основе данных переписи могут получиться не гомогенными (в одну страту попадут люди с разными доходами). Например, такими, которые представлены в таблице 13.
Таблица 13.
Распределение респондентов по стратам.
| № группы. | Респонденты, попавшие в группу. |
| 1. | A,F,C. |
| 2. | L,J,D. |
| 3. | K,E,G. |
| 4. | H,B,I. |
В этом случае практически никакой выгоды по сравнению с собственно-случайной выборкой стратифицированный отбор не принесет, т.к. вероятность отбора нами плохих выборок сохранится и здесь.
Пример: [6, 42-46] Теперь рассмотрим случай с неоднородной генеральной совокупностью, т.е. совокупностью, в которой существуют отдельные резкие отклонения от средней тенденции. Например, генеральная совокупность, представленная в таблице 1, будет неоднородной, если, к примеру, респондент B вместо дохода в 6300 будет получать доход в 20000.
Стратифицировать в этом случае можно двумя путями: так, как было стратифицировано в таблице 12 и так, как это сделано в таблице 14.
Таблица 14.
Распределение респондентов по стратам.
| № группы. | Респонденты, попавшие в группу. |
| 1. | A,J,D,L. |
| 2. | G,F,I,H. |
| 3. | C,E,K. |
| 4. | B. |
В первом случае, как уже было сказано, был проведен пропорциональный отбор, а в данном случае - соответственно непропорциональный. Пропорциональный отбор в данном случае (в случае с неоднородной генеральной совокупностью) не годится, т.к. он не обеспечит однородность страт (в какую бы страту ни попал B, эта страта сразу же станет неоднородной).
Однако при непропорциональном отборе нарушается принцип равной вероятности попадания в выборку, т.к. респондент B попадает в нашу выборку при любом исходе.
Для исправления этого обстоятельства при непропорциональном отборе применяется процедура взвешивания. Взвешивание призвано «восстановить» Взвешиванием мы увеличиваем удельный вес респондентов из больших страт. Для нашего примера средняя будет рассчитываться следующим образом:
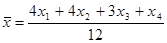
Если отобрать все возможные выборки при данной стратификации (таб. 14), то без взвешивания мы получим смещенную выборочную оценку (генеральная средняя = 3817, а выборочная средняя = 6852). Однако если произвести взвешивание, то в данном случае непропорциональный отбор (стандартное отклонение = 277) будет эффективнее пропорционального (стандартное отклонение = 1878).
Пример:
Рассмотрим далее рассмотренный выше пример с микрорайонами. Решение проблемы может состоять в увеличении объема выборки или в проведении случайного опроса. Но последнее может привести к некоторым искажениям и неточностям, т.к. микрорайоны отличаются также и между собой. Первое же связано с дополнительными расходами.
Здесь нам на помощь может прийти стратифицированная выборка. Ее можно осуществить если нам удастся объединить несколько микрорайонов как сходные. Разделив все микрорайоны на несколько относительно однородных групп, можно построить репрезентативную выборку, не увеличивая ее объем.
Стратифицированная выборка может помочь нам и тогда, когда нет полного списка жителей города. В этом случае можно из каждой страты выбрать один микрорайон, в котором будет проводиться опрос, и собрать информацию о его жителях.
Однако если мы неправильно выберем критерии для объединения микрорайонов, то это приведет к серьезной систематической ошибке.






