В общем случае параметры первичной обмотки трансформатора отличаются от параметров вторичной обмотки. Эта разница наиболее ощутима при больших коэффициентах трансформации, что затрудняет расчеты и построение векторных диаграмм, так как в этом случае векторы электрических величин первичной обмотки значительно отличаются по своей длине от одноименных векторов вторичной обмотки. Указанные затруднения устраняются приведением всех параметров трансформатора к одинаковому числу витков, обычно к числу витков первичной обмотки w1. С этой целью все величины, характеризующие вторичную цепь трансформатора, – ЭДС, напряжение, ток и сопротивления – пересчитывают на число витков w1 первичной обмотки с учётом коэффициентом трансформации 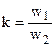 , трансформатор с
, трансформатор с  , где
, где  . Такой трансформатор называют приведенным. При этом его энергетические показатели: все мощности и фазовые сдвиги во вторичной обмотке приведенного трансформатора должны остаться такими, как и в реальном трансформаторе.
. Такой трансформатор называют приведенным. При этом его энергетические показатели: все мощности и фазовые сдвиги во вторичной обмотке приведенного трансформатора должны остаться такими, как и в реальном трансформаторе.
Так, электромагнитная мощность вторичной обмотки реального трансформатора Е2I2 должна быть равна электромагнитной мощности вторичной обмотки приведенного трансформатора:
 . (1.27)
. (1.27)
Подставив значение приведенного тока вторичной обмотки 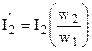 в (1.27), получим формулу приведенной вторичной ЭДС:
в (1.27), получим формулу приведенной вторичной ЭДС:
 . (1.28)
. (1.28)
Так как  , то приведенное напряжение вторичной обмотки
, то приведенное напряжение вторичной обмотки
 . (1.29)
. (1.29)
Из условия равенства потерь в активном сопротивлении вторичной обмотки имеем  . Определим приведенное активное сопротивление:
. Определим приведенное активное сопротивление:
 . (1.30)
. (1.30)
Приведенное индуктивное сопротивление рассеяния вторичной обмотки определяют из условия равенства реактивных мощностей  откуда
откуда
 . (1.31)
. (1.31)
Приведенное полное сопротивление вторичной обмотки трансформатора
 . (1.32)
. (1.32)
Приведенное полное сопротивление нагрузки, подключенной на выводы вторичной обмотки, определим по аналогии с (1.32):
 . (1.33)
. (1.33)
Уравнения напряжений и токов для приведенного трансформатора имеют вид
 ;
;
 ; (1.34)
; (1.34)
 .
.
Эти уравнения устанавливают аналитическую связь между параметрами трансформатора во всем диапазоне нагрузок от режима х.х. до номинальной.
Еще одним средством, облегчающим исследование электромагнитных процессов и расчет трансформаторов, является применение электрической схемы замещения приведенного трансформатора. На рис. 33, а представлена эквивалентная схема приведенного трансформатора, на которой сопротивления r и x условно вынесены из соответствующих обмоток и включены последовательно им. В приведенном трансформаторе k = 1, а поэтому  . В результате точки А и а, а также точки X и x: на схеме имеют одинаковые потенциалы, что позволяет электрически соединить указанные точки, получив Т–образную схему замещения приведенного трансформатора (рис. 33, б). В электрической схеме замещения трансформатора магнитная связь между цепями заменена электрической.
. В результате точки А и а, а также точки X и x: на схеме имеют одинаковые потенциалы, что позволяет электрически соединить указанные точки, получив Т–образную схему замещения приведенного трансформатора (рис. 33, б). В электрической схеме замещения трансформатора магнитная связь между цепями заменена электрической.

Рис. 33. Эквивалентная схема (а) и схема замещения (б) приведенного трансформатора
Схема замещения приведенного трансформатора удовлетворяет всем уравнениям ЭДС и токов приведенного трансформатора (1.34) и представляет собой совокупность трех ветвей: первичной – сопротивлением  и током
и током  ; намагничивающей – сопротивлением
; намагничивающей – сопротивлением  и током
и током  ; вторичной – с двумя сопротивлениями: сопротивлением собственно вторичной ветви
; вторичной – с двумя сопротивлениями: сопротивлением собственно вторичной ветви  и сопротивлением нагрузки
и сопротивлением нагрузки  и током
и током  . Изменением сопротивления нагрузки
. Изменением сопротивления нагрузки  на схеме замещения могут быть воспроизведены все режимы работы трансформатора.
на схеме замещения могут быть воспроизведены все режимы работы трансформатора.
Параметры ветви намагничивания  определяются током х.х. Наличие в этой ветви активной составляющей rm обусловлено магнитными потерями в трансформаторе.
определяются током х.х. Наличие в этой ветви активной составляющей rm обусловлено магнитными потерями в трансформаторе.
Все параметры схемы замещения, за исключением  , являются постоянными для данного трансформатора и могут быть определены из опыта х.х. и опыта к.з.
, являются постоянными для данного трансформатора и могут быть определены из опыта х.х. и опыта к.з.






