ИМПУЛЬСНЫХ СИГНАЛОВ СЛОЖНОЙ ФОРМЫ
Цель работы: ознакомление с переносчиком информации на основе периодической последовательности импульсных сигналов сложной формы (ИССФ), изучение некоторых свойств частотных спектров ИССФ и их применение для рассматриваемого переносчика в информационных системах.
1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Применение ИССФ в качестве переносчика информации в информационно-вычислительных, измерителльно-вычислительных, а также в управляющих вычислительных комплексах различного назначения (в машиностроении, медицине, физике и т. д.) позволяет получить ряд новых свойств, отличающих его от других переносчиков.
В отличие от широко известного переносчика на основе периодической последовательности прямоугольных импульсов (ПППИ) (рис. 1, а) в переносчике на основе ИССФ вместо одиночных прямоугольных импульсов (рис. 1, а) используются периодически повторяющиеся группы импульсов (рис. 1, б), параметры которых (амплитуда, длительность, фаза, их количество) выбираются соответствующим образом для получения определённых свойств ИССФ. На этом рисунке рассмотрен случай амплитудно-импульсной модуляции первого рода (АИМ-1), хотя возможны и другие известные виды импульсной модуляции.
 |
Рис. 1
ИССФ могут быть образованы суммой как несмещенных относительно друг друга (перекрывающихся во времени), так и смещенных (неперекрывающихся во времени) ПППИ. В первом случае элементарные импульсы разных ПППИ должны иметь разные длительности. Во втором случае длительности элементарных импульсов разных ПППИ могут быть как разными, так и одинаковыми.
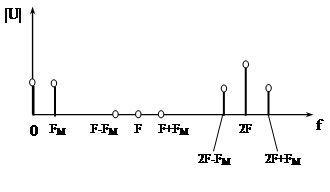 |
Применение ИССФ в качестве переносчика информации позволяет подавить в спектре модулированного сигнала (рис. 2) заданное число спектральных зон (спектральной зоной называют k-ю гармонику спектра с частотой kF и боковыми составляющими вокруг нее с частотами kF+Fм и kF-Fм, где F - частота повторения ИССФ, Fм - максимальная частота в спектре модулирующего сигнала). Постоянную составляющую и составляющую с частотой Fм будем называть нулевой спектральной зоной.
Рис.2
Какие конкретно спектральные зоны должны быть подавлены, зависит от решаемой задачи.
При восстановлении (демодуляции) непрерывных сигналов с помощью фильтров нижних частот необходимо в спектре ИССФ оставить нулевую спектральную зону, в которой находятся составляющие демодулируемого сигнала. В этом случае при подавлении нескольких спектральных зон, начиная с первой и далее, т. е. k=1,2,...,n-1, появляется возможность расширить спектр модулирующего сигнала.
Для согласования спектров передаваемых сигналов с полосой частот пропускания каналов связи, имеющих искажения (завал) АЧХ в области низких частот, необходимо подавить несколько первых спектральных зон, включая нулевую.
1.1. ФОРМИРОВАНИЕ ИССФ ИЗ НЕСМЕЩЕННЫХ ПППИ 
Если последовательность ИССФ образована из суммы n несмещенных ПППИ, то в спектре такой последовательности можно подавить n - 1 спектральных зон.
Число элементарных импульсов, из которых будет состоять сформированный ИССФ, определится как M=2n - 1.
Спектральные зоны, начиная с первой, будут подавлены при определенных соотношениях амплитуд Uiи длительностей tiимпульсов соответствующих ПППИ. Для расчета указанных параметров исходных импульсов необходимо решить систему из (n-1) уравнений [1]:

 k=1, 2,...,
k=1, 2,...,  n-1. (1)
n-1. (1)
Обратите внимание на то, что число уравнений в системе равно числуподавляемых спектральных зон, а число слагаемых в каждом уравнении равно числу исходных ПППИ.
Система уравнений (1) не имеет однозначного решения относительно амплитуд и длительностей ПППИ. Обычно, исходя из простоты технической реализации, длительности импульсов задают таким образом, чтобы отношение Т/tiбыло целым числом, а для еще большего упрощения, чтобы оно было степенью 2. Однако и в этом случае число уравнений в системе (1) меньше числа неизвестных на единицу. Поэтому необходимо задаться амплитудой импульсов одной из исходных ПППИ, например U1. При этих ограничениях решение системы (1) относительно Uiстановится единственным. При выборе амплитуд элементарных импульсов ИССФ необходимо учитывать допустимый диапазон изменения сигнала на входе преобразователей.
Представление непрерывных сигналов при дискретизации импульсными сигналами сложной формы дает ряд преимуществ по сравнению с представлением обычными ПППИ:
· снижение требований к фильтрам нижних частот при восстановлении непрерывных сигналов фильтрационным способом;
· возможность расширения частотного диапазона дискретизируемого сигнала при заданном периоде дискретизации Т;
· возможность согласования спектра ИССФ с полосой частот пропускания некоторых типов преобразователей и каналов связи.
1.2. ФОРМИРОВАНИЕ ИССФ ИЗ СМЕЩЕННЫХ ПППИ
Обратите внимание на то, что одна из исходных ПППИ представляет собой несмещенную последовательность одиночных импульсов с амплитудой Uo, а остальные ПППИ образованы из сдвоенных импульсов с амплитудами Ui, расположенных на временной оси симметрично относительно импульса несмещенной ПППИ на время ±ti.
Если последовательность ИССФ образована из суммы одной несмещенной ПППИ и n дополнительных смещенных ПППИ, состоящих из сдвоенных импульсов каждая, то в спектре такой последовательности можно подавить постоянную составляющую и n - 1 первых спектральных зон, т.е. всего n спектральных зон. Это обеспечивает согласование спектра ИССФ и полосы частот пропускания преобразователей или каналов связи, имеющих искажения амплитудно-частотных характеристик в области низких частот.
Еще раз обратите внимание на то, что n в данном случае - это число дополнительных ПППИ, содержащих пары импульсов, смещенных относительно импульсов начальной ПППИ, содержащей одиночные импульсы.
Число элементарных импульсов, из которых будет состоять сформированный ИССФ, определится как M=2n + 1.
Спектральные зоны будут подавлены при определенных соотношениях амплитуд Uiи длительностей tiимпульсов соответствующих ПППИ.
Исходя из удобства формирования ИССФ длительности всех элементарных импульсов исходных ПППИ выбирают одинаковыми и равными t, а временные сдвиги парных импульсов i-й ПППИ относительно импульса начальной ПППИ выбирают равными ti= it. При этом ИССФ будет состоять из соприкасающихся друг с другом элементарных импульсов.

|
Для расчета указанных параметров исходных импульсов необходимо решить приведенную ниже систему уравнений [1]:
(2)
Обратите внимание на то, что число уравнений в системе равно числуподавляемых спектральных зон, включая нулевую, т.е. равно n, а число слагаемых в каждом уравнении равно общему числу исходных ПППИ, т. е. n+1.
2. ПОДГОТОВКА К РАБОТЕ
2.1. РАСЧЕТ ПАРАМЕТРОВ ПППИ
Порядок расчета параметров исходных ПППИ рассмотрим на конкретных примерах. При подготовке к работе варианты исходных данных (номер варианта соответствует номеру бригады) взять из пункта 2.3.
2.1.1.Формирование ИССФ из несмещенных ПППИ (пример ):
n = 3 - число исходных ПППИ;
T = 1 - период повторения ИССФ (период дискретизации);
U1 = 1 - амплитуда импульсов первой исходной ПППИ;
t1 = T/4 - длительность импульсов первой исходной ПППИ;
t2 = T/8 - длительность импульсов второй исходной ПППИ;
t3 = T/16 - длительность импульсов третьей исходной ПППИ.
Перед решением системы уравнений в среде MathCAD необходимо задать начальные значения неизвестных. Начальное значение первого неизвестного приравнивают к значению амплитуды первой ПППИ, начальные значения остальных неизвестных задают произвольно:
u1 = U1, u2 = 6, u3 = -4.5.
Задание системы уравнений для расчета амплитуд импульсов второй (и далее) ПППИ в системе MathCAD должно начинаться словом Given и кончаться словом find:
Given
u1 sin(p t1/T) + u2 sin (p t2/T) + u3 sin (p t3/T) = 0,
u1 sin(p 2t1/T) + u2 sin(p 2t2/T) + u3 sin(p 2t3/T) =0,
u = find(u2, u3) - в скобках перечисляются неизвестные, подлежащие определению,

 -8.886
-8.886
u = - результат вычисления.
13.807
Таким образом, в результате расчета получили амплитуды импульсов каждой из исходных ПППИ:
U1 = U1 = 1, U2 = u0 = -8.886, U3 = u1 = 13.807.
2.1.2. Формирование ИССФ из смещенных ПППИ (пример):
n = 2 - число дополнительных ПППИ, смещенных относительно начальной ПППИ;
T = 1 - период повторения ИССФ (период дискретизации);
A0 =1 - амплитуда импульсов несмещенной (начальной) исходной ПППИ;
t = T/8 - длительность импульсов всех ПППИ;
a0 = A0, a1 = -7, a2 = 8 - задание начальных значений неизвестных.
Решение системы уравнений:
Given
a0 + 2 (a1 + a2) = 0,
a0 + 2 (a1 cos(2 p 1 t/T) + a2 cos(2 p 2 t/T)) =0,
a = find (a1, a2).

 -0.707
-0.707
a = - результат решения системы уравнений.
0.207
Амплитуды импульсов каждой из исходных ПППИ:
A0 = a0 = 1, A1 = a0 = -0.707, A2 = a1 = 0.207.
2.2. Описание ИССФ средствами MathCAD
При описании используются заданные временные параметры и рассчитанные амплитуды импульсов исходных ПППИ.
2.2.1. Формирование ИССФ из несмещенных ПППИ.
Задать число К и номера k отсчетов сигнала во временной области (число К выбрать равным степени 2, что необходимо для обеспечения работоспособности встроенной функции MathCAD fft(x) - вычисления БПФ. Например, K:=512 k:=0.. K-1.
Задать “текущее”время MathCAD для представления ПППИ в виде векторов: dt1:= T1/K - шаг “текущего” времени,
t1k:= dt1×k - “текущее” время MathCAD.
Задать исходные ПППИ во временной области. Для этого можно воспользоваться следующей формой описания прямоугольного импульса:
s1 k:= if (t1 k £ 0, 0, if (t 1k £ t1, U1, 0)) - первая исходная ПППИ;
s2 k:= if (t1 k £ (t1-t2)/2, 0, if (t1 k £ (t1-t2)/2 +t2, U2, 0)) - вторая исходная ПППИ;
s3 k:= if (t1 k £ (t1-t3)/2, 0, if (t1k £ (t1-t3)/2 + t3, U3, 0)) - третья исходная ПППИ;
s k:= s1 k + s2 k +s3 k - сформированный ИССФ.
2.2.2. Формирование ИССФ из смещенных ПППИ.
Задать “текущее”время MathCAD для представления ПППИ в виде векторов: dt2:= T2/K - шаг “текущего” времени,
t2k:= dt2×k - “текущее” время MathCAD.
Для описания исходной несмещенной ПППИ можно воспользоваться следующей конструкцией:
S0 k:= if (t2 k £ n × t, 0, if (t2 k £ (n+1) × t, A0, 0)),
где n - число дополнительных ПППИ, состоящих из пары импульсов каждая, один из которых смещен на t влево от исходной ПППИ, а второй - на t вправо.
Описание каждой из дополнительных ПППИ можно выполнить с помощью выражений:
S j1 k:= if (t2 k £ (n- j)× t, 0, if (t2 k £ (n+1 - j)× t, A j, 0)) - cмещенная влево ПППИ,
S j2 k:= if(t2 k £ (n+j)× t, 0, if (t2 k £ (n+1+ j)× t, A j, 0)) - смещенная вправо ПППИ,
где j = 1, 2,..., n - номер дополнительной ПППИ,
A j - амплитуда импульсов дополнительной ПППИ,
S j k:= S j1 k + S j2 k - j-я смещенная ПППИ,
S k:= S0 k + S1 k + S2 k +... - сформированный ИССФ.
Примечание: для предотвращения возможных ошибок в описании ИССФ, сформированных из несмещенных и смещенных ПППИ, одноименные временные параметры обозначены разными переменными: для несмещенных ПППИ Т1, dt1, t1k, а для смещенных ПППИ T2, dt2, t2k.
2.3. Варианты заданий
2.3.1. Варианты сигналов
| № варианта | Подавляемые спектральные зоны | Отношение периода Т к длительности импульсов t | Период T, мкс | U1 или А0, В |
| 0, 1 0, 1, 2 0, 1 0, 1, 2 0, 1 0, 1 1, 2 1, 2, 3 2, 3 1, 2, 3 | 16:1 20:1 8:1 16:1 10:1 12:1 (2:4:16):1 (2:4:8:32):1 (2:4:16):1 (2:4:8:16):1 (3:10):1 (4:6):1 | 2.5 |
В вариантах 1...6 ИССФ формируется из смещенных ПППИ, а в вариантах 7...12 - из несмещенных ПППИ.
2.3.2. Варианты заданий
| № задания | Сигналы из п. 2.3.1 | № задания | Сигналы из п. 2.3.1 |
| 1, 7 2, 11 3, 9 4, 12 5, 8 6, 10 | 1, 10 2, 12 3, 7 4, 11 5, 8 6, 9 |
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
3.1. В среде MathCAD ввести выражения, описывающие порядок расчета параметров исходных ПППИ, и выражения, описывающие во времени эти ПППИ и сформированный ИССФ. Построить графики исходных ПППИ и ИССФ, используя результаты предварительных расчетов из пп. 2.1, 2.2.
3.2. Рассчитать спектральные составляющие ИССФ, используя встроенную функцию MathCAD fft(x), осуществляющую быстрое преобразование Фурье над вектором x, число элементов которого равно степени 2:
3.2.1. задать номера спектральных составляющих n:= 0.. K/2;
3.2.2. выполнить операцию БПФ для ИССФ из несмещенных ПППИ:
srektr1:= fft(s)
и для ИССФ из смещенных ПППИ:
spektr2:= fft (S);
3.2.3. определить амплитуды спектральных составляющих ИССФ:
mod1 n:= | spektr1 n | и mod2 n:= | spektr2 n |;
3.2.4. определить частоты спектральных составляющих:
f n:= n / T.
3.3. Построить спектры амплитуд сформированных ИССФ.
3.4. Рассчитать спектральные составляющие каждой из исходных ПППИ, образующих соответствующие ИССФ.
Перекрывающиеся ПППИ:
спектрs1:= fft(s1), спектрs2:= fft(s2), спектрs3:= fft(s3).
Неперекрывающиеся ПППИ:
спектрS0:= fft(S0), спектрS1:= fft(S1), спектрS2:= fft(S2).
3.5. Сложить спектры ПППИ, образующих каждый ИССФ, и определить амплитуды спектральных составляющих каждого из полученных спектров:
sum1 n:= спектрs1 n + спектрs2 n + спектрs3 n,
sum2 n:= спектрS0 n + спектрS1 n + спектрS2 n,
Ампл1 n:= | sum1 n |,
Ампл2 n:= | sum2 n |.
3.6. Построить спектры амплитуд и сравнить со спектрами амплитуд соответствующих ИССФ.
4. СОДЕРЖАНИЕ ОТЧЕТА
4.1. Краткие теоретические сведения о переносчике информации на основе ИССФ.
4.2. Расчет длительностей и амплитуд импульсов исходных ПППИ.
4.3. Описание исходных ПППИ и ИССФ средствами MathCAD.
4.4. Временные диаграммы исходных ПППИ и ИССФ.
4.5. Графики спектров амплитуд ИССФ.
4.6. Графики спектров амплитуд исходных ПППИ.
4.7. График спектра амплитуд, полученного из суммы спектров исходных ПППИ.
5. КОНТРОЛЬНЫЕ ВОПРОСЫ
5.1. Какое свойство преобразования Фурье используется при формировании ИССФ?
5.2. Преимущества, которые дает переносчик информации на основе ИССФ.
5.3. Как согласовать спектры ИССФ с полосой частот пропускани преобразователей и каналов связи, имеющих искажения амплитудно-частотных характеристик в области низких частот?
5.4. Из скольких элементарных импульсов будет состоять ИССФ при его формировании из:
· перекрывающихся во времени ПППИ;
· неперекрывающихся во времени ПППИ?
5.5. Сколько спектральных зон в спектре ИССФ можно подавить в случае, если этот сигнал будет сформирован из n ПППИ:
· перекрывающихся во времени;
· не перекрывающихся во времени?
5.6. Сколько уравнений должна содержать система для расчета параметров исходных ПППИ, и сколько слагаемых должно быть в каждом уравнении, если ИССФ формируется из n ПППИ?
5.7. Как расширить спектр модулирующего сигнала при заданном периоде следования ИССФ?
Карасев В. В., Михеев А. А., Нечаев Г. И. Измерительные системы для вращающихся узлов и механизмов / Под ред. Г. И. Нечаева. М.: Энергоатомиздат, 1996. С. 76 - 87.
Содержание
Предисловие………………………………………………………………...1
Лабораторная работа № 1.
Дискретизация непрерывных сигналов по времени……………………..1
Лабораторная работа № 2.
Переносчик информации на основе импульсных сигналов
сложной формы……………………………………………………………11






