ПРЕДИСЛОВИЕ
Методические указания содержат описания двух лабораторных работ: «Дискретизация непрерывных сигналов по времени» и Переносчик информации на основе импульсных сигналов сложной формы» (ИССФ).
Эти работы проводятся по курсам «Теория сигналов в информационных системах» (специальность 071900), преобразование биомедицинских сигналов», «Методы обработки биомедицинских сигналов и данных» (специальность 190500) в целях углубления знаний по соответствующим разделам лекционного материала.
Обе работы выполняются в классе ПЭВМ с использованием пакета прикладных программ MathCAD.
Лабораторная работа № 1
ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ ПО ВРЕМЕНИ
Цель работы: изучение принципа представления непрерывных (аналоговых) сигналов в виде отдельных мгновенных значений (отсчетов, выборок) и практическое использование этого принципа при дискретизации аналоговых сигналов по времени и по уровню.
1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Аналоговые сигналы являются типичными на входах информационно-вычислительных и измерительно-вычислительных комплексов (ИВК), а также управляющих вычислительных комплексов (УВК). Физической величиной, определяющей характер сигнала, обычно является напряжение (или ток), изменяющееся по определенному закону, отображающему тот или иной процесс. Например, в нефтеперерабатывающих установках технологические процессы характеризуются, в частности, давлением и температурой. В медицине также имеют дело с аналогичными процессами: артериальное давление и температура тела. Независимо от физической природы процессов и сигналов их при теоретическом рассмотрении заменяют математическим представлением в виде некоторой функции, описывающей закон изменения во времени S(t), заложенной в реальном процессе или сигнале.
В современных ИВК и УВК входные аналоговые сигналы преобразуются в цифровые. При этом для исходных сигналов необходимо осуществить, по крайней мере, две операции. В результате первой операции аналоговые сигналы представляются в виде отдельных мгновенных значений (отсчетов, выборок), то есть осуществляется дискретизация сигналов по времени. Вторая операция обеспечивает преобразование аналоговых сигналов в цифровые за счет дискретизации (квантования) полученных отсчетов по уровню.
Для сигналов, частотный спектр которых ограничен полосой частот от нуля до Fм, применима фундаментальная теорема В. А. Котельникова. В соответствии с этой теоремой аналоговый сигнал S(t), не содержащий частот выше Fм, полностью определяется своими мгновенными значениями S(kТ), k=1,2,3,…, взятыми через интервалы времени
 .(1) .(1)
|
Смысл теоремы Котельникова состоит в том, что для передачи непрерывной функции времени S(t) с ограниченным спектром достаточно передать лишь ее отдельные мгновенные значения, отсчитанные через интервалы времени T. Мгновенные значения (отсчеты) функции S(t), взятые в точках T, 2T, 3T,... и т. д., полностью определяют ход непрерывной функции.
При этом сигнал S(t) аналитически представляется рядом Котельникова [1]:
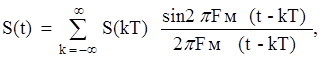
|
(2)
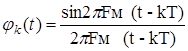
в котором - так называемая функция k-го
отсчета (рис. 1).

Рис. 1
Из выражения (2) следует, что непрерывная функция времени S(t) равна сумме бесконечного числа непрерывных слагаемых. Каждое слагаемое представляет собой функцию типа sinx/x, называемую функцией отсчета. Значение k-й функции отсчета в момент времени t=kT определяется амплитудой отсчета S(kT) в этот же момент времени, а во всех остальных точках отсчетов равно нулю (см. рис. 1).
Строго говоря, сигналы с ограниченным спектром должны бесконечно продолжаться во времени. Любой реальный сигнал имеет конечную продолжительность во времени, поэтому должен иметь бесконечно протяженный, но обычно быстро затухающий спектр. Поэтому с той или иной точностью можно считать спектр ограниченным некоторой предельной частотой Fм. Обычно эта частота определяется на основе энергетического критерия. При этом спектр ограничивается областью частот от 0 до Fм, в которой сосредоточена подавляющая часть энергии сигнала (до 90 – 99 %, а иногда и более). Такое ограничение спектра, естественно, приводит к искажению сигнала. Связь практической ширины спектра с учитываемой долей энергии сигнала определяется равенством Парсеваля. Квадрат относительной погрешности воспроизведения сигнала может быть определен из соотношения:
 |
где S(f) – спектральная характеристика сигнала,
Ес – полная энергия сигнала,
Ех – энергия отброшенной части спектра сигнала.
Все вышесказанное позволяет ввести идеализацию, заключающуюся в том, что все реальные непрерывные сигналы можно рассматривать как функции с ограниченным спектром, то есть как функции, спектр которых не содержит частот выше некоторой граничной частоты Fм. Таким образом, теорему Котельникова можно применять практически ко всем реальным сигналам.
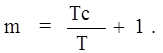
|
Если сигнал существенно отличается от нуля только в интервале времени Тс, имеет спектр, ограниченный частотой Fм, то в соответствии с теоремой Котельникова число дискретных отсчетов m, которые можно взять из сигнала в интервале Тс:
Обычно m>>1, поэтому с учетом выражения (1) получим m=2FмTc.
 (3) (3)
|
В этом случае непрерывный сигнал u(t) приближенно можно заменить рядом Котельникова с конечным числом членов:
Приближенность выражения (3) объясняется тем, что при конечном числе членов ряда значение суммы точно совпадает с мгновенными значениями функции S(t) только в точках отсчетов. В интервалах между этими точками значения функции S(t) и суммы конечного числа членов ряда различаются. Таким образом, появляется погрешность представления непрерывной функции времени суммой конечного числа членов ряда, которая имеет наибольшее значение на краях интервала Тс и наименьшее в середине этого интервала (рис. 2).

Рис. 2
Величина m определяет число независимых дискретных отсчетов, которыми можно заменить непрерывный сигнал. Это число m называют числом степеней свободы сигнала или базой сигнала. Отсчеты называют координатами сигнала.
Из теоремы Котельникова следуют два важных вывода:
1) передача непрерывных сигналов, в принципе, ничем не отличается от передачи цифровых сигналов, так как передачу непрерывной функции времени можно заменить передачей дискретной во времени последовательности ее мгновенных отсчетов, которые легко преобразуются в цифровой код;
2) можно организовать многоканальную передачу сигналов от нескольких источников аналоговой информации (первичных преобразователей) путем передачи в интервалах между отсчетами одного из непрерывных сигналов отсчетов других непрерывных сигналов. В частности, в современных ИВК уплотняется до нескольких сотен и тысяч источников аналоговых сигналов с целью последующей обработки в одной ЭВМ. В системах связи передача многоканального сигнала осуществляется по одной физической линии связи. Высокая стоимость ЭВМ и линии связи делает многоканальное преобразование и многоканальную передачу экономически целесообразными.
Значение периода дискретизации, определяемое выражением (1), является предельным максимальным значением. В реальных устройствах период дискретизации обычно имеет меньшее значение. Это обусловлено особенностями восстановления непрерывного сигнала по его дискретным отсчетам (вопросы восстановления непрерывного сигнала будут изучаться в следующих лабораторных работах).
Большее, чем определяемое по выражению (1), значение периода дискретизации приведет к появлению в нулевой спектральной зоне спектра дискретизированного сигнала составляющих с частотами ниже Fм, которых не было в исходном сигнале. Частота самой низкочастотной из этих новых составляющих равна Fопр - Fм, где Fопр=1/Т - частота опроса непрерывного сигнала.
Данное обстоятельство приведет к погрешности восстановленного сигнала, обусловленной так называемыми интермодуляционными искажениями.
2. ПОДГОТОВКА К РАБОТЕ
Лабораторная работа состоит из двух частей:
1) представление непрерывного сигнала рядом Котельникова;
2) исследование спектров дискретизированных сигналов и последствий нарушения условия теоремы Котельникова.
2.1. Варианты заданий (номера вариантов соответствуют номеру бригады).
2.1.1. Исходный непрерывный сигнал представляет собой половину периода синусоидального сигнала S(t)=sin(2pF1ct+j), т.е. текущее время t изменяется от 0 до 1/2F1c. Значение начальной фазы выбрать из таблицы1.
Таблица 1
| № | ||||||||||||
| j | p/6 | p/4 | p/3 | 2p/3 | 3p/4 | 5p/6 | -p/6 | -p/4 | -p/3 | -2p/3 | -3p/4 | -5p/6 |
2.1.2. Исходный непрерывный сигнал представляет собой сумму гармоник и постоянной составляющей Uo. “Лишняя” гармоника, добавляемая к исходному сигналу, нарушает условие теоремы Котельникова.
Состав исследуемого сигнала выбрать из таблицы 2.
Таблица 2
| № вари-анта | F2c, Гц | Номера гармоник | Амплитуды гармоник, В | Uo, В | “Лишняя” гармоника Номер U, В |
| 1, 3, 5 | 1, 0.3, 0.2 | 10 1 | |||
| 1, 3 | 2, 0.5 | 6 0.8 | |||
| 1, 4 | 0.2, 0.4 | 9 0.6 | |||
| 2, 3, 6 | 1, 2, 0.4 | 2.5 | 9 1.5 | ||
| 1, 4, 7 | 1, 0.3, 0.2 | 11 1.5 | |||
| 1, 3, 5 | 1, 0.5, 0.3 | 1.5 | 10 2 | ||
| 2, 4 | 1, 2 | 11 1.5 | |||
| 3, 8 | 1, 1 | 20 1.7 | |||
| 1, 9, 12 | 2, 1, 1.5 | 17 0.5 | |||
| 1, 2 | 1, 0.5 | 5 1.5 | |||
| 4, 8, 9 | 1, 2, 3 | 18 2.5 | |||
| 2, 4, 6, | 6, 3, 2 | 9 1 |
2.2. Описание исходного сигнала средствами MathCAD для первой части работы.
2.2.1. Задать длительность сигнала Т1с:= 1/2F1c. Для всех вариантов F1c: = 1 Гц.
2.2.2. Задать число отсчетов К для описания сигнала средствами MathCAD. MathCAD работает с векторами и матрицами, поэтому исходный сигнал дожен быть представлен в виде вектора, элементами которого являются значения отсчетов в k-х точках исходного сигнала. Чем больше этих отсчетов, т.е. чем больше К, тем точнее будет описан исходный сигнал средствами MathCAD. Для того чтобы можно было использовать функцию быстрого преобразования Фурье fft(s), следует задавать К равным степени 2 (в работе задать К:= 128).
2.2.3. Задать номера отсчетов MathCAD k:= 0.. K-1.
2.2.4. Задать интервалы дискретности времени dt1:= T1c/K.
2.2.5. Задать “текущее” время в MathCAD t1 k := kdt1.
2.2.6. Записать выражение для исходного сигнала, заменив текущее время t на “текущее” время t1 k ,
S1 k := sin(2pF1ct1 k+j).
2.3. Описание исходного сигнала для второй части работы.
2.3.1. Задать длительность сигнала T2с: = 1/F2c, где F2c - частота первой гармоники.
2.3.2. Повторить пункты 2.2.2 - 2.2.5, заменив T1c, dt1 и t1k на T2c, dt2 и t2 k.
2.3.3. Записать выражение для исходного сигнала, например:
S2 k := 2sin(2p F2c t2 k)+0.5sin(2p 3F2c t2 k)+0.3sin(2p 5F2c t2 k)+1.5.
2.4.Описаниедискретизированного сигнала для первой части работы.
2.4.1. Определить период дискретизации.
Для определения частоты дискретизации необходимо знать максимальную частоту в спектре исходного сигнала. Пренебрежем всеми составляющими спектра исходного сигнала, амплитуды которых менее 0.1 амплитуды первой гармоники.
Выполнить следующие действия.
1) Задать номера частотных составляющих исходного сигнала n:=0.. K/2.
2) Вычислить спектральные составляющие исходного сигнала, выполнив быстрое преобразование Фурье от вектора S1, sp1:= fft(S1).
3) Вычислить модули спектральных составляющих msp1n:=|sp1n|.
4) Определить номер Np последней учитываемой составляющей, используя сделанное выше допущение. Учитывая особенности вычислений в системе MathCAD (требование целочисленности индексных переменных), взять в качестве Np ближайшее большее целочисленное значение, равное степени числа 2.
5) Вычислить максимальную частоту в спектре сигнала F1max:=Np/T1c.
6) Вычислить период дискретизации по Котельникову Т1o:=1/2F1max.
2.4.2. Задание дискретных отсчетов исходного сигнала.
1) Вычислить число отсчетов, которыми может быть представлен непрерывный сигнал M1:= 2 T1c F1max+1.
2) Вычислить “относительный период”, т.е. число интервалов dt1, через которое будут следовать дискретные отсчеты преобразуемого сигнала, M1o:= Т1o/dt1 .
3) Задать номера дискретных отсчетов j1:= 0.. M1.
4) Задать номера исходных отсчетов MathCAD, которые будут приняты в качестве дискретных отсчетов преобразуемого сигнала m1 j1: = j1 M1o.
5) Задать элементы матрицы, состоящей из k строк и M столбцов (один столбец матрицы соответствует одному из отсчетов):
S1mk, j1: = if (k = m1j1 , S1k , 0).
6) Образовать вектор длины К, соответствующий дискретизированному сигналу:
S1dk:= å S1m k , j1.
j1
Амплитуда каждого отсчета равна значению непрерывного сигнала в соответствующий момент времени, между дискретными отсчетами сигнал равен нулю.
7) Образовать вектор длины М1, содержащий значения дискретных отсчетов исходного сигнала
DOS1 j1:= å S1m k, j1.
k
2.5. Описание дискретизированного сигнала для второй части работы.
2.5.1. Рассчитать период дискретизации.
1) Определить самую высокочастотную гармонику, входящую в состав вашего сигнала, т.е. F2max.
2) Вычислить период дискретизации по Котельникову
Т2o:= 1/2 F2max.
2.5.2. Задание дискретных отсчетов исходного сигнала.
1) Вычислить число отсчетов, которыми может быть представлен непрерывный сигнал M2:= 2T2cF2max+1. При исследовании спектров диск-ретизированных сигналов в данной работе используется встроенная функция MathCAD fft(S), осуществляющая быстрое преобразование Фурье и требующая, чтобы вектор s содержал число элементов, равное степени 2. Поэтому в качестве числа отсчетов М2 следует принять ближайшее к расчетному большее целочисленное значение, равное степени числа 2.
2) Уточнить значение периода дискретизации Т2o:= T2c/M2.
3) Вычислить “относительный период”, т.е. число интервалов dt2, через которое будут следовать дискретные отсчеты преобразуемого сигнала M2o:= Т2o/dt2.
4) Задать номера дискретных отсчетов j2:= 0.. M2.
5) Задать номера исходных отсчетов MathCAD, которые будут приняты в качестве дискретных отсчетов преобразуемого сигнала m2 j2: = j2 M2o.
6) Задать элементы матрицы, состоящей из k строк и M2 столбцов (один столбец матрицы соответствует одному из отсчетов)
S2mk, j2: = if (k = m2 j2 , S2k , 0).
7) Образовать вектор длины К, соответствующий дискретизированному сигналу. Амплитуда каждого отсчета равна значению непрерывного сигнала в соответствующий момент времени, между дискретными отсчетами сигнал равен нулю.
S2dk:= å S2m k , j2.
J2
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
3.1. Представление непрерывного сигнала рядом Котельникова.
3.1.1. В среде MathCAD ввести исходный сигнал S1 k. Построить график исходного сигнала S1 k = f(t1 k).
3.1.2. Ввести выражение, описывающее сигнал S1d k. Построить график дискретизированного сигнала S1d k = f(t1 k).

|
3.1.3. Вычислить функцию отсчета, соответствующую по времени j-му дискретному отсчету.
3.1.4. Устранить неопределенность типа 0/0.
f1 k, j1:= if(t1 k = j1 ×T1o, 1, f k, j1).
3.1.5. Построить график одной из функций отсчетов f1 k, j1 = f (t1 k).
3.1.6. Записать выражение для ряда Котельникова

|
.
3.1.7. Построить на одном графике зависимости:
S1 k = f(t1 k ) и S K k = f (t1 k).
3.1.8. Вычислить погрешность представления непрерывного сигнала конечным числом членов ряда Котельникова DS k:= S1 k - SK k .
3.1.9. Построить график DS k = f (t1 k).
3.2. Исследование спектров дискретизированных сигналов.
3.2.1. В среде MathCAD ввести исходный сигнал S2 k. Построить график исходного сигнала S2 k = f(t2 k).
3.2.2. Ввести выражение, описывающее сигнал S2d k. Построить график дискретизированного сигнала S2d k = f(t2 k).
3.2.3. Рассчитать спектральные составляющие дискретизированного сигнала.
1) Задать номера спектральных составляющих n:= 0.. K/2.
2) Выполнить операцию быстрого преобразования Фурье
Sp2d:= fft (S2d).
3) Определить модуль каждой спектральной составляющей
mSp2 n:= | Sp2d n |.
4) Определить частоты спектральных составляющих f2 n:= n/T2c.
5) Построить спектр амплитуд mSp2 n = f (f2 n).
6) Добавить к исходному сигналу S2 k “лишнию” гармонику в соответствии с вариантом задания. Сравнить частоту “лишней” гармоники с частотой дискретизации.
7) Выполнить действия 2 - 5 настоящего пункта.
8) Сравнить спектры сигналов, продискретизированных в соответствии с условием теоремы Котельникова и с нарушением данного условия.
4. СОДЕРЖАНИЕ ОТЧЕТА
4.1. Цель работы и краткие теоретические сведения.
4.2. Выражения, описывающие средствами MathCAD исходные и дискретизированные сигналы.
4.3. Графики исходных и дискретизированных сигналов.
4.4. Выражения, описывающие процесс представления непрерывного сигнала рядом Котельникова и погрешность такого представления.
4.5. Совмещенный график исходного сигнала и его представления рядом Котельникова с ограниченным числом членов.
4.6. График погрешности представления непрерывного сигнала конечным числом членов ряда Котельникова.
4.7. Спектры амплитуд сигнала, продискретизированного в соответствии с теоремой Котельникова, и сигнала, продискретизированного с нарушением условия данной теоремы.
5. КОНТРОЛЬНЫЕ ВОПРОСЫ
5.1. Сформулируйте теорему В. А. Котельникова.
5.2. Выводы из теоремы В. А. Котельникова.
5.3. Свойства функции отсчета.
5.4. Поясните процесс восстановления непрерывного сигнала по его дискретным отсчетам с помощью ряда Котельникова.
5.5. Объясните график погрешности представления непрерывного сигнала конечным числом членов ряда Котельникова.
5.6. Объясните, в чем отличие спектров амплитуд дискретизированных сигналов: исходного и с “лишней” гармоникой.
5.7. К чему приводит нарушение условия теоремы Котельникова при выборе частоты дискретизации
Дмитриев В. И. Прикладная теория информации. М.: Высш. школа, 1989. С. 63 - 81.
Лабораторная работа № 2






