Любое сообщение представляет собой совокупность сведений о некоторой физической системе. Например, на вход системы управления средствами противовоздушной обороны может быть передано сообщение о том, что на определенном аэродроме в данный момент находится определенное количество истребителей в боевой готовности, или что аэродром выведен из строя огнем противника и т.п. Любое из приведенных сообщений описывает состояние физической системы. Но при известном заранее состоянии физической системы не имеет смысла передача сообщения – оно приобретает смысл только тогда, когда состояние системы случайно. В качестве объекта, о котором передается информация, рассматривается некоторая физическая система X, которая случайным образом может в каком-либо состоянии – систему, которой присуща некоторая степень неопределенности. Сведения, полученные о системе тем содержательнее, чем больше была неопределенность системы до получения этих сведений (априори). Каким образом измеряется степень неопределенности? Степень неопределенности физической системы определяется не только числом ее возможных состояний, но и вероятностями состояний. Теперь рассмотрим некоторую систему X, принимающую конечное множество состояний: 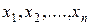 с вероятностями
с вероятностями  , где
, где  , вероятность того, что система X примет состояние xi (
, вероятность того, что система X примет состояние xi (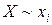 обозначается событие: система находится в состоянии
обозначается событие: система находится в состоянии  ). Очевидно также, что
). Очевидно также, что  .
.
Энтропия определяется как мера неопределенности состояния некоторой физической системы. В результате получения сведений неопределенность системы может быть уменьшена. Чем больше объем полученных сведений, чем они более содержательны, тем больше будет информация о системе, тем менее неопределенным будет ее состояние. Поэтому количество информации измеряют уменьшением энтропии той системы, для уточнения состояния которой предназначены сведения.
Рассмотрим некоторую систему X, над которой производится наблюдение. Оценим информацию, получаемую в результате того, что состояние системы X становится полностью известным. До получения сведений (априори) энтропия системы была H (X); после получения сведений состояние системы полностью определилось, т.е. энтропия стала равной нулю. Обозначим через Ix информацию, получаемую в результате выяснения состояния системы X. Она равна уменьшению энтропии:  или
или
 , (1.1)
, (1.1)
т.е. количество информации, приобретаемое при полном выяснении состояния некоторой физической системы, равно энтропии этой системы.
Представим (1.1) в виде:
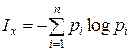 , (1.2)
, (1.2)
Где  .
.
Формула (1.2) означает, что информация Ix есть осредненное по всем состояниям системы значение логарифма вероятности состояния с обратным знаком. Действительно, для получения Ix каждое значение 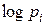 (логарифм вероятности i -го состояния) со знаком «-» умножается на вероятность этого состояния и все такие произведения складываются. Каждое отдельное слагаемое -
(логарифм вероятности i -го состояния) со знаком «-» умножается на вероятность этого состояния и все такие произведения складываются. Каждое отдельное слагаемое - 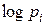 рассматривать как частную информацию, получаемую от отдельного сообщения, состоящего в том, что система X находится в состоянии xi. Обозначим эту информацию через
рассматривать как частную информацию, получаемую от отдельного сообщения, состоящего в том, что система X находится в состоянии xi. Обозначим эту информацию через 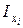 :
:
 . (1.3)
. (1.3)
Тогда информация Ix представляется как средняя (или полная) информация, получаемая от всех возможных отдельных сообщений с учетом их вероятностей. Перепишем формулу (1.2) в форме математического ожидания:
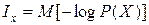 , (1.4)
, (1.4)
Где X – любое (случайное) состояние системы X.
Так как все числа pi не больше единицы, то как частная информация 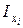 , так и полная
, так и полная  не могут принимать отрицательные значения. Если все возможные состояния системы обладают различными вероятностями, информации от разных неодинаковы: наибольшую информацию несут сообщения о тех событиях, которые априори были наименее вероятны.
не могут принимать отрицательные значения. Если все возможные состояния системы обладают различными вероятностями, информации от разных неодинаковы: наибольшую информацию несут сообщения о тех событиях, которые априори были наименее вероятны.
Пример. На шахматной доске в одной из клеток произвольным образом поставлена фигура. Априори все положения фигуры на доске одинаково вероятны. Необходимо определить информацию, получаемую от сообщения, в какой именно клетке находится фигура.
Решение. Энтропия системы X с n равновероятными состояниями равна 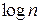 ; в данном случае:
; в данном случае: 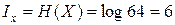 (дв.ед.), т.е. сообщение содержит 6 двоичных единиц информации. Т.к. все состояния системы равновероятны, то ту же информацию несет и любое конкретное сообщение типа: фигура находится в квадрате e2.
(дв.ед.), т.е. сообщение содержит 6 двоичных единиц информации. Т.к. все состояния системы равновероятны, то ту же информацию несет и любое конкретное сообщение типа: фигура находится в квадрате e2.
Пример. В условиях предыдущего примера определить частную информацию от сообщения, что фигура находится в одной из угловых клеток доски.
Решение. Априорная вероятность состояния, о котором сообщается, равна 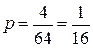 . Частная информация равна
. Частная информация равна 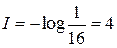 (дв.ед.).
(дв.ед.).
В термодинамике энтропия обозначается через S.  , где Q – теплота, T – температура.
, где Q – теплота, T – температура.
 , где E – энергия системы, F – свободная энергия системы.
, где E – энергия системы, F – свободная энергия системы.
Пусть  - некоторое конечное распределение вероятностей, т.е. набор неотрицательных чисел, удовлетворяющих условию:
- некоторое конечное распределение вероятностей, т.е. набор неотрицательных чисел, удовлетворяющих условию: 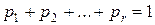 .
.
Энтропией этого распределения называется величина  , (1.5)
, (1.5)
где 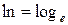 и
и  . Очевидно, что
. Очевидно, что 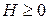 , причем H =0 тогда и только тогда, когда все вероятности
, причем H =0 тогда и только тогда, когда все вероятности 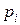 , кроме одной, равны 0.
, кроме одной, равны 0.
Функция 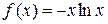 ,
, 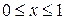 , выпукла кверху и
, выпукла кверху и 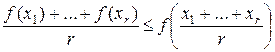 . Следовательно,
. Следовательно, 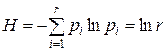 .
.
Иначе, энтропия достигает своего максимального значения при 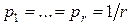 . «Степень неопределенности» в свершении того или иного события различна для различных распределений. (Если
. «Степень неопределенности» в свершении того или иного события различна для различных распределений. (Если 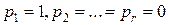 , то нет неопределенности и в результате опыта произойдет событие A 1. Если
, то нет неопределенности и в результате опыта произойдет событие A 1. Если 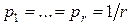 , распределение обладает максимальной неопределенностью).
, распределение обладает максимальной неопределенностью).






