Очевидно, что такого порядка изменения длины с частотой 70 раз в минуту невозможны и их на самом деле нет. Если бы такое происходило, наше тело вообще не могло бы функционировать. Достаточно только представить себе, что такое происходит с сосудами мозга.
К счастью, на самом деле продольные удлинения в находящихся под давлением трубах всех видов и размеров много меньше, чем можно было бы ожидать или опасаться. Доказательством того, что дело обстоит именно таким образом, является так называемый коэффициент Пуассона.
Если вы натянете резиновую ленту, она станет заметно тоньше, то же самое происходит и со всеми другими твердыми телами, хотя для большинства материалов это не так бросается в глаза. Напротив, если вы уменьшите длину куска материала, сжав его, поперечные размеры увеличатся. И то и другое происходит благодаря действию упругих сил, и первоначальная форма тела восстанавливается при снятии нагрузки.
Мы не замечаем этих поперечных перемещений в таких веществах, как сталь или кость, в силу малости как продольной, так и поперечной деформаций, но фактически и здесь дело обстоит точно так же. То обстоятельство, что подобные эффекты характерны для всех твердых тел и такое поведение существенно для практических задач, было впервые отмечено французом С.Д. Пуассоном (1781-1840). Он родился в очень бедной семье и в детстве не получил сколько-нибудь систематического образования, но в возрасте тридцати одного года стал академиком, а во Франции это одна из наивысших почестей, и он удостоился ее за свои работы в области теории упругости. Как было сказано в гл. 2, закон Гука гласит, что модуль Юнга = E = (напряжение / деформация) = s/e.
Поэтому, если мы приложим к плоской пластинке растягивающее напряжение s1, она удлинится упругим образом, так что в направлении растяжения деформация будет иметь величину e1 = s1 / E.
Однако, кроме того, пластинка сократится в поперечном направлении (то есть в направлении под прямым углом к напряжению s1), и величину соответствующей деформации мы обозначим e2. Пуассон обнаружил, что для каждого материала отношение деформаций e1 и e2 есть величина постоянная, и это отношение теперь принято называть коэффициентом Пуассона. Ниже мы всюду будем использовать для этой величины обозначение ν. Таким образом, для данного материала, подвергаемого простому одноосному нагружению напряжением s1, ν = e2 / e1 = коэфициент Пуассона[50]
Деформацию e1 в направлении напряжения s1 можно назвать первичной деформацией, а деформацию e2, вызванную напряжением s1 в перпендикулярном ему направлении, - вторичной деформацией (рис. 55). Согласно этому, e2 = ν e1, а так как e1 = s1 / E (это - закон Гука), то e2 = ν s1 / E.

Рис. 55. При одноосном нагружении твердого тела растягивающим напряжением s1 тело испытывает в направлении этого нагружения деформацию e1, а в поперечном направлении сокращается, при этом деформация равна e2.
Таким образом, если мы знаем значения величин ν и E, мы можем вычислить и первичную, и вторичную деформации.
Для материалов, используемых в технике, таких, как металлы, камень и бетон, значения ν лежат всегда между 1/4 и 1/3. Для твердых биологических материалов значения коэффициента Пуассона обычно выше, и часто они лежат вблизи 1/2. Преподаватели элементарной теории упругости сказали бы вам, что коэффициент Пуассона не может принимать значений больше 1/2, иначе происходили бы разного рода абсурдные и неприемлемые вещи. Это справедливо лишь отчасти, и значения коэффициента Пуассона для некоторых биологических материалов являются очень высокими, часто они больше единицы[51]. Экспериментальное значение коэффициента Пуассона для моего живота, измеренное недавно мною в ванне, составляет примерно единицу (см. сноску выше).
Таким образом, как сказано выше, благодаря коэффициенту Пуассона, если мы растягиваем в каком-либо одном направлении кусок материала, такой, как пленка или стенка артерии, он удлиняется в этом направлении, но одновременно сокращается в перпендикулярных. Поэтому в случаях, когда растягивающее напряжение действует не в одном, а в двух взаимно перпендикулярных направлениях, возникающие деформации будут разностью тех деформаций, которые создало бы каждое из этих напряжений в отдельности, и окажутся поэтому меньше последних.
При одновременном действии напряжений s1 и s2 суммарная деформация в направлении действия s1 будет e1 = (s1 - ν s2)/ E, а суммарная деформация в направлении действия s2 будет e2 = (s2 - ν s1)/ E.
Отсюда, используя результаты, приведенные в гл. 5[52], с учетом коэффициента Пуассона получаем, что продольная деформация стенок трубы, находящейся под внутренним давлением и сделанной из материала, подчиняющегося закону Гука, будет e2 = (rp/2tE)(1 - 2ν), где r - радиус, р - давление, t - толщина стенок.
В результате увеличение длины трубы оказывается значительно меньшим, чем можно было бы ожидать; для гуковского же материала с коэффициентом Пуассоны, равным 1/2, продольные перемещения вообще отсутствуют. В действительности, как говорилось выше, материал стенок артерий не подчиняется закону Гука, в то же время коэффициент Пуассона для него, вероятно, больше 1/2. Возможно, эти два фактора взаимно компенсируются, поскольку соответствующие удлинения, фактически наблюдаемые в эксперименте, очень малы[53]. Несомненно, тот факт, что артерии постоянно находятся в организме в натянутом состоянии, свидетельствует о мерах предосторожности, принятых Природой против любых возможных остаточных удлинений кровеносных сосудов.
Эффекты, связанные с коэффициентом Пуассона, по-видимому, играют важную роль в поведении тканей животных; но они важны и в технике, о чем свидетельствуют все новые факты, возникающие, как правило, неожиданно и в самых разных сочетаниях.
Возможно, следует также добавить, что, в то время как аорта и главные артерии расширяются и сокращаются упругим образом в такт с биением сердца, с артериями меньшего размера дело обстоит несколько иначе. Стенки этих артерий соединены с мышечной тканью, которая может увеличивать их эффективную жесткость и таким образом, ограничивая диаметр этих артерий, влиять на количество крови, подводимое к каждому из участков тела. Таким путем регулируется кровоснабжение тела.
(обратно)
Надежность, или о вязкости тканей животных
У животных довольно часто случаются переломы костей и разрывы сухожилий; упругие свойства костей и сухожилий отличаются от свойств тканей, рассматриваемых в этой главе. Примечательно, однако, что механические разрушения мягких тканей животных происходят довольно редко. На это имеется несколько причин. Шкура и мягкие части тела животного, будучи очень нежесткими, могут не получить серьезных повреждений при ударе; подвергаясь большим деформациям, животное отделывается только синяками. Более интересен, однако, вопрос о концентрации напряжений, поскольку мягкие ткани животных практически не боятся концентрации, этой главной причины катастроф инженерных сооружений. Ткани животных не требуют большого коэффициента запаса, поэтому конструктивная эффективность, то есть выдерживаемая конструкцией нагрузка, приходящаяся на единицу веса конструкции, может быть очень высокой.
Такой иммунитет к концентрации напряжений определяется отнюдь не мягкостью тканей и малым модулем Юнга. Резина тоже мягкая, и ее модуль Юнга тоже очень мал, однако все мы помним с детства, как выпущенные в сад воздушные шарики очень скоро с шумом лопались, наткнувшись на шипы первого же куста. Детьми мы не понимали, что из-за концентрации напряжений и малой величины работы разрушения от прокола в натянутой резине очень быстро распространяется трещина, а если бы и понимали, то вряд ли это уменьшило бы наши огорчения. Перепонка же крыла летучей мыши ведет себя иначе, хотя также сильно натягивается в полете. При проколе крыла разрыв от этого места распространяется редко и повреждение скоро заживает, несмотря на то что мышь не перестает летать.
Объяснение этого кроется, я думаю, в существенных различиях упругих свойств и величин работы разрушения резины и биологических тканей. В настоящее время данные о работе разрушения мягких биологических тканей, по существу, отсутствуют, однако зависимости напряжения от деформации в большинстве случаев известны очень хорошо, а между формой этих зависимостей и работой разрушения, по-видимому, имеется тесная связь.
Интересный пример составляет пленка куриного яйца - пленка, которую мы видим за завтраком сразу под скорлупой вареного яйца. Это одна из немногих биологических мембран, которые подчиняются закону Гука, в данном случае - вплоть до деформаций около 24%, когда происходит разрыв пленки. Простой (правда, грозящий легкими неприятностями) эксперимент с сырым яйцом показывает, что эта пленка легко рвется. Так, конечно, и должно быть, поскольку иначе цыпленку было бы трудно вылупиться из яйца. Между прочим, округлая форма самой скорлупы такова, что ее трудно разрушить снаружи, но легко разбить изнутри.
Яичная пленка - ткань, по-видимому, исключительная; по самому своему предназначению она подлежит разрушению после того, как сделает свое дело, сохранив в яйце влагу и защитив его от инфекции. Вероятно, именно по этой причине она обладает, как мы говорили, особыми упругими свойствами. Однако упругие свойства подавляющего большинства мягких тканей совершенно другие, их характеризует зависимость, показанная на рис. 53, и, для того чтобы выполнять свое назначение, большинству из этих тканей необходимо быть "вязкими". На практике оказывается, что материалы с зависимостью напряжения от деформации подобного типа рвутся с очень большим трудом; следует заметить, что внутренние причины этого не вполне ясны. Одна из причин, возможно, состоит в том, что запасаемая упругая энергия, которая может идти на развитие трещины (а она дается площадью под кривой деформирования - см. гл. 4), меньше, чем для других типов кривой деформирования[54].
Как мы уже говорили, упругое поведение большинства тканей животных близко к показанному на рис. 53. Должен сознаться, когда я впервые обратил на это внимание, мне показалось, что это некая странность или причуда Природы, которая, увы, не смогла придумать ничего лучшего, не получив приличного инженерного образования. Однако после довольно путаных попыток исследовать проблему на основе грубых расчетов мне становится все более ясным, что в случаях, когда конструктивная система должна надежно работать, испытывая действительно большие обратимые деформации, такая зависимость напряжения от деформации - единственно приемлемая. Появление тканей животных с такого типа кривой деформирования было весьма важным для эволюции и существования высших форм жизни. Биологам это полезно иметь в виду.
(обратно)
Строение мягких тканей
Отчасти, возможно, по указанным причинам молекулярная структура тканей животных редко напоминает структуру резины или синтетических полимеров. Строение большинства тканей животных очень сложное, чаще всего они являются составными (композитными) и включают по крайней мере два компонента. В их состав входит сплошная фаза, или матрица, в которой распределены армирующие ее прочные нити, или волокна, из другого вещества. Во многих случаях эта сплошная фаза содержит вещество, называемое эластином, который имеет очень малый модуль Юнга и кривую деформирования такого типа, как показана на рис. 56. Другими словами, по своим упругим свойствам эластин лишь на одну ступеньку отличается от жидкостной пленки с поверхностным натяжением. Эластин, однако, армирован прочными зигзагообразными волокнами коллагена (рис. 56а), представляющего собой разновидность протеина - вещества, близкого к веществу сухожилий и имеющего большой модуль Юнга и почти гуковское поведение. Вследствие того что армирующие волокна сильно перекручены, они вносят очень малый вклад в сопротивление материала растяжению при малых деформациях, и упругое поведение материала в этом случае весьма близко к поведению эластина. Однако по мере того, как композитная ткань вытягивается, коллагеновые волокна постепенно становятся все более туго натянутыми, и, таким образом, модуль Юнга материала в растянутом состоянии будет определяться модулем Юнга коллагена. Описанное поведение материала более или менее соответствует кривой, изображенной на рис. 53.
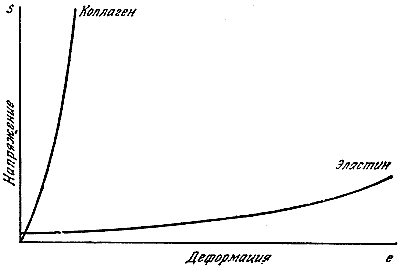
Рис. 56. Примерный вид кривых деформирования эластина и коллагена.
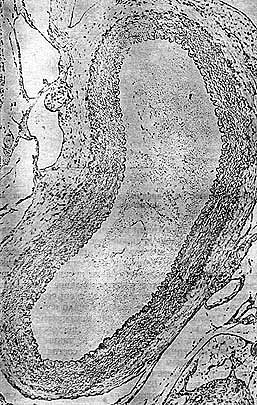
Рис. 56а. Поперечный разрез артерии под микроскопом. Упругие свойства артерии обеспечивает эластин, укрепленный перекрученными коллагеновыми нитями. (Артерии, освобожденные от крови, делаются плоскими.)
Роль коллагеновых волокон не сводится только к увеличению жесткости ткани при больших деформациях, они, по-видимому, нужны и для того, чтобы обеспечить "вязкость" ткани, то есть ее трещиностойкость. Когда на живой ткани возникает порез в результате травмы или под действием скальпеля, на первой стадии процесса заживления на заметных расстояниях вокруг раны коллагеновые волокна временно исчезают. Только после того, как полость раны заполняется эластином, коллагеновые волокна образуются вновь и восстанавливается полная первоначальная прочность ткани. Этот процесс может продолжаться 3 или 4 недели, и пока он не закончится, величина работы разрушения ткани в окрестности раны чрезвычайно мала. Поэтому, если в течение двух-трех недель после хирургической операции требуется вновь вскрыть зашитую полость, в этом месте бывает трудно наложить надежные швы.
Коллаген существует в различных формах, в частности, он может состоять из перекрученных нитей протеиновых молекул. Его сопротивление деформированию определяется главным образом натяжением связей между атомами в молекулах, и потому он ведет себя, по Гуку, подобно нейлону или стали. А почему эластин ведет себя почти так же, как пленки жидкости с поверхностным натяжением? Краткий ответ на этот вопрос состоит в том, что на самом деле этого никто не знает. Однако профессоры Вейс-Фог и Андерсен выдвинули предположение, что такое поведение может быть обязано некоей модифицированной форме поверхностного натяжения. Согласно их гипотезе эластин состоит из сети гибких длинных цепочек молекул, находящихся внутри эмульсии. Капельки жидкости в составе эмульсии смачивают эти молекулярные цепочки, в то время как основное вещество эмульсии их не смачивает. В связи с этим молекулярным цепям энергетически выгодно почти по всей их длине свернуться в клубки внутри капелек жидкости (рис. 57, а). При действии растягивающих нагрузок они вытягиваются из капель и распрямляются (рис. 57, б)[55].
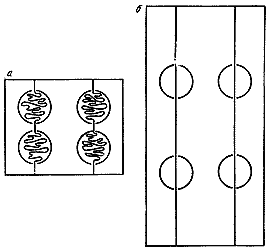
Рис. 57. Предполагаемое строение эластина. а - недеформированное состояние, цепи молекул находятся главным образом в скрученном состоянии внутри капелек; б - деформированное состояние, цепи молекул вытянуты из капелек.
Наше тело состоит по большей части из мышц, являющихся биологически активной тканью, способной сокращаться и тем самым вызывать растяжения сухожилий и других тканей. Мышцы, однако, содержат коллагеновые нити, упругие свойства которых могут играть только пассивную роль. Если растягивать умерщвленную мышцу, получается зависимость напряжения от деформации, опять-таки очень похожая на приведенную на рис. 53, и представляется вероятным, что коллаген в мышце несет функцию ограничения ее растяжения в расслабленном состоянии. Другими словами, он действует как некий тормоз, обеспечивающий безопасность.
Как мы уже говорили, другое назначение коллагеновых волокон в тканях - это обеспечить сравнительно большую величину работы разрушения. Для животных это хорошо, но это неудобно для людей, которые едят мясо. Другими словами, именно коллаген делает мясо "вязким". Однако представляется, что Природа не на стороне вегетарианцев, поскольку она, к ее мудрости, устроила так, что коллаген превращается в желатин - вещество, обладающее в жидком состоянии малой прочностью, при такой температуре, которую еще выдерживает эластин, или мышечная ткань. Поэтому процесс приготовления пищи заключается в превращении большей части коллагеновых волокон в желатин (представляющий собой желеобразную массу) с помощью жарения, варки или кипячения. Таким образом, мы имеем здесь дело с наукой, укрепляющей веру в мудрость Природы.
(обратно) (обратно) (обратно)
Часть III. Конструкции в условиях сжатия и изгиба
Глава 8
Стены, арки и плотины, или башни, уходящие в облака, и устойчивость каменной кладки
Что б ты построить из кубиков мог?
Замки и виллы, церковь и док.
Детский цветник стихов
Р. Л. Стивенсон
Как мы уже убедились, простых смертных, не наделенных сверхъестественным разумом Природы, на пути создания конструкций, подвергающихся растяжениям, подстерегают трудности, осложнения и хитроумные ловушки. Особенно это относится к случаям, когда мы хотим создать конструкцию из нескольких кусков материала и сталкиваемся с проблемой прочности соединений. Не случайно наши предки старались по возможности избегать конструкций, подвергающихся растяжениям, и стремились использовать такие конструкции, в которых всюду действуют только сжимающие нагрузки.
Этому требованию лучше всего удовлетворяет каменная кладка. Тот замечательный успех, который во все времена сопутствовал ее применению, обязан двум факторам. Первый вполне очевиден - это возможность избежать растягивающих напряжений, особенно в соединениях. Второй менее очевиден - это удивительная совместимость задач конструирования больших строений, сложенных из камней, с ограниченностью возможностей "донаучного" подхода.
Из всех конструкций самых различных видов только каменные сооружения допускают слепое копирование традиционных пропорций, которой не ведет автоматически к беде. Именно поэтому на протяжении всей истории строения из камня далеко превосходили по своим размерам и внушительности все остальное, что было создано руками человека. Желание строить теряющиеся в облаках башни и величественные храмы уходит своими корнями в глубины истории и даже в предысторию человечества. Эпиграфом к началу этой книги послужили строки из книги Бытие о Вавилонской башне. Напомним, что там говорилось о намерении построить "башню, высотою до небес". Впрочем, я думаю, ни один богослов не задавался вопросом, какой высоты можно было бы ее построить на самом деле.
Почти вся нагрузка, приходящаяся на стены такой башни, определялась бы их собственным весом, и можно вычислить то напряжение сжатия, которое создавала бы у основания башни действующая вертикально вниз статическая нагрузка каменной кладки. В этом случае предельной явилась бы та минимальная высота башни, при которой ее кирпичи были бы раздавлены приходящимся на них весом.
Плотность камня и кирпича составляет около 2500 кг/м3, а их прочность на сжатие, вообще говоря, несколько больше 5 кгс/мм2 или 50 МН/м2.
Элементарный расчет показывает, что высоту башни с вертикальными стенами можно довести до 2 км, и кирпичи в ее основании все еще не будут раздавлены. Башня же, имеющая суживающиеся кверху стены, могла бы быть значительно выше; примерно такой принцип избрала Природа для горообразования. Высота Джомолунгмы около 9 км, и пока не похоже, чтобы она собиралась обвалиться. Так что суживающаяся кверху башня простой формы с широким основанием вполне могла бы быть доведена до такой высоты, на которой людям Сеннаара стало бы трудно дышать из-за нехватки кислорода, прежде чем статическая нагрузка ее стен раздавила бы кирпичи в основании.
Хотя в такого рода вычислениях не содержится ничего принципиально неправильного, в действительности высота всех построенных когда-либо башен и близко не доходила до теоретически предельной. Так, самое высокое из существующих сегодня зданий, Нью-йоркский центр международной торговли, лишь на 400 м возвышается над землей, да и это для нас не самый удачный пример, поскольку, подобно всем небоскребам, оно построено из стали. Пирамида Хеопса и шпили самых высоких кафедральных соборов достигают немногим более 150 м, и лишь некоторые из огромного множества каменных строений достигают хотя бы половины этой высоты, подавляющее же большинство зданий намного ниже.
Поэтому обычно напряжения сжатия, возникающие в каменной кладке под действием ее собственного веса, весьма малы. Как правило, они редко превышают 0,01 прочности камня на сжатие и на практике не накладывают ограничений на высоту зданий или на их прочность. Тем не менее известно, что, начиная с библейской Силоамской башни, которая, не будучи особенно высокой, упала и убила 18 человек, они все же время от времени неожиданно рушатся (несмотря на уверенность архитекторов и строителей в их прочности). Такое происходило во все времена, а иногда происходит и сегодня. И под тяжестью каменной кладки (а она немалая) нередко гибнут люди.
Но если стены рушатся не под давлением сжимающих напряжений, так под действием чего? Ответить на этот вопрос помогают детские игры. Все мы в детстве строили башни из кубиков, довольно неустойчивым образом поставленных друг на друга. Достигнув некоторой высоты, такое сооружение неизменно разваливалось. Даже дети понимают, хотя и не могут выразить этого в научных терминах, что виной тому отнюдь не сжимающие напряжения. Эти напряжения на деле ничтожно малы, а башня опрокидывается потому, что ее стены не строго вертикальны. Другими словами, речь здесь должна идти не о недостатке прочности, а о недостатке устойчивости. Хотя разница между этими двумя понятиями очевидна маленьким детям, она не всегда ясна строителям и архитекторам и тем более историкам искусства, которые пишут о кафедральных соборах и подобных им сооружениях.
(обратно)
Линии давлений и устойчивость стен
Внушает трепет и благоговенье
Весь облик этой каменной громады.
Уходят в небо древние колонны,
Главами мраморными подпирая
Изогнутый дугою тяжкий свод.
Недвижно все, покоем дышит камень
И, ужасая, привлекает взор.
Утренний мост
Уильям Конгрив
Во времена королевы Анны культурная жизнь Англии не могла быть особенно разрозненной и можно быть почти уверенным в том, что Конгрив (1670-1729) имел беседы и делил застолье с Ванбруфом, автором многочисленных пьес и создателем Бленхеймского дворца, а также с самим Кристофером Реном. Для этих людей в общих чертах было совершенно ясно, что устойчивость зданий определяет не столько прочность камня и скрепляющего "раствора", сколько распределение их веса.
Однако одно дело понимать это и совсем другое - конкретно представлять себе все в деталях и уметь определить заранее, будет ли здание безопасным или нет. Чтобы достичь научного понимания того, как ведет себя каменная кладка, ее необходимо рассматривать как упругий материал, то есть следует учесть то обстоятельство, что материал камня деформируется под действием нагрузки и что он подчиняется закону Гука. Полезно также, хотя это и не абсолютно необходимо, использовать понятия напряжения и деформации.
На первый взгляд все же, конечно, кажется невероятным, что твердый кирпич и камень могут деформироваться в сколько-нибудь заметной степени под действием нагрузки, создаваемой зданием. И в самом деле, еще столетие после Гука к этой мысли не могли привыкнуть даже строители, архитекторы и инженеры. Они упорно игнорировали закон Гука и считали каменную кладку абсолютно жесткой. В результате их расчеты оказывались неверными и здания иногда рушились.
Однако в действительности модуль Юнга для кирпича и камня не очень велик (в этом можно убедиться, посмотрев на изогнутые колонны собора в Солсбери на рис. 4), а потому упругие перемещения каменной кладки отнюдь не так малы, как можно было бы предполагать. Даже стены обычного небольшого дома сжаты в вертикальном направлении своим собственным весом примерно на миллиметр. В больших зданиях эти перемещения, естественно, значительно больше. А когда вам кажется, что дом сотрясается под порывами сильного ветра, это не так далеко от истины. Верхушка небоскреба Эмпайр стэйт билдинг раскачивается при сильном ветре более чем на 0,5 м[57].
Современный расчет каменной кладки основан на простом законе Гука, а также на следующих четырех допущениях, которые оказываются справедливыми на практике:
1) сжимающие напряжения столь малы, что материал не может разрушаться за счет сжатия (мы уже обсуждали этот вопрос);
2) благодаря использованию строительного раствора или цемента соединения выполнены достаточно тщательно, так что силы сжатия действуют по всей площади соединения, а не в нескольких выступающих точках;
3) трение в соединениях столь велико, что не может произойти разрушения конструкции вследствие взаимного проскальзывания кирпичей или камней (на самом деле никаких проскальзываний до разрушения конструкции не происходит);
4) соединения не обладают сколько-нибудь заметной прочностью на растяжение; даже если случайным образом раствор обладает некоторой прочностью на разрыв, на нее нельзя полагаться и ею следует пренебречь.
Таким образом, назначение строительного раствора состоит не в том, чтобы "склеивать" кирпичи или камни, а в том, чтобы сжимающие нагрузки передавались через соединение более равномерно.
Насколько мне известно. Юнг был первым, кто стал учитывать упругие деформации каменной кладки. Он рассмотрел, что происходит в прямоугольном блоке каменной кладки, скажем в участке стены, когда он подвергается действию вертикальной сжимающей нагрузки Р. Мы приведем его рассуждения в упрощенной форме, переведя их для этого на язык напряжений и деформаций, которого во времена Юнга, конечно, не существовало.
До тех пор пока нагрузка P действует вертикально вниз в плоскости симметрии, то есть посредине стены, кладка будет сжата равномерно и, согласно Гуку, соответствующее распределение сжимающих напряжений по толщине стены также будет равномерным (рис. 58).

Рис. 58. Нагрузка P действует в плоскости симметрии стены.
Рис. 59. Нагрузка P действует в пределах "средней трети" стены.
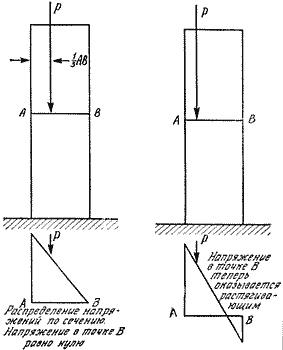
Рис. 60. Нагрузка P действует на краю "средней трети" соединения AB.
Рис. 61. Нагрузка P действует вне "средней трети" соединения AB.
Предположим теперь, что вертикальная нагрузка P немного сместилась в сторону и действует не точно в плоскости симметрии стены. В этом случае сжимающее напряжение не будет постоянным вдоль ее сечения: для того чтобы в точности уравновесить действующую нагрузку, оно должно быть с одной стороны больше, чем с другой. Юнг показал, что если материал подчиняется закону Гука, то напряжения по толщине стены будут изменяться линейно и распределение напряжений будет выглядеть так, как показано на рис. 59.
Пока что соединению, которое мы видим на рис. 59, ничто не угрожает: по всему сечению АВ действуют только сжимающие напряжения. Однако если приложение нагрузки сместится еще дальше от середины стены - на границу так называемой "средней трети" стены, то возникнет ситуация, изображенная на рис. 60, в которой распределение напряжений имеет треугольную форму и сжимающее напряжение на одном из краев соединения обращается в нуль.
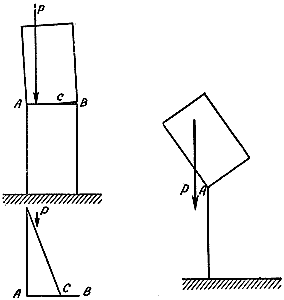
Рис. 62. Вот что происходит, если возникает ситуация, изображенная на рис. 61. В соединении возникает трещина ВС, и вся нагрузка теперь распределена по площади, соответствующей отрезку АС, - эффективная толщина стены уменьшается.
Рис. 63. Если линия действия нагрузки проходит за пределами отрезка АВ, то стена будет поворачиваться вокруг точки A, - опрокинется и упадет.






