Точного уравнения для описания поведения термистора не существует, – имеются только приближенные. Рассмотрим два широко используемых приближенных уравнения.
Первое приближенное уравнение, экспоненциальное, вполне удовлетворительно для ограниченных температурных диапазонов, в особенности – при использовании термисторов с малой точностью. Второе уравнение, называемое уравнением Стейнхарта-Харта, обеспечивает прекрасную точность для диапазонов до 100 оС.
Сопротивление термистора с отрицательным ТКС уменьшается приблизительно по экспоненте с увеличением температуры. В ограниченных температурных диапазонах его R-T-зависимость достаточно хорошо описывается следующим уравнением:
RT2=RT1 е b (I/T2 – I/T1),
Где Т1 и Т2 – абсолютные температуры в градусах Кельвина (оС +273);
RT1 и RT2 – сопротивления термистора при Т1 и Т2; b - константа, определяемая путем измерения сопротивления термистора при двух известных температурах.
 |
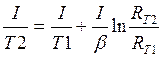Если b и RT1 известны, то это уравнение можно преобразовать и использовать для вычисления температуры, измеряя сопротивление:
Бета является большим, положительным числом и имеет размерность в градусах Кельвина. Типовые значения изменяются от 3000 до 5000 оК.
Изготовители часто включают значения для бета в спецификации, однако, так как экспоненциальное уравнение является лишь приблизительным, значение бета зависит от двух температур, использованных при его вычислении. Некоторые изготовители используют значения 0 и 50 оС; другие – 25 и 75 оС.
Можно использовать другие температуры: можно вычислить самостоятельно значение бета на основании таблиц зависимости сопротивления от температуры, которые предлагает изготовитель. Уравнение, как правило согласуется с измеренными значениями в пределах ± 1 оС на участке в 100 оС. Уравнение нельзя использовать с достоверностью при температурах, сильно отличающихся от тех, что были использованы для определения бета.
Перед тем, как перейти к уравнению Стейнхарта-Харта, рассмотрим два других параметра, часто используемых для описания термисторов: альфа (a) и коэффициент сопротивления. Альфа просто определяется наклоном R-T- кривой, то есть является чувствительностью при определенной температуре. Альфа обычно выражается в «процентах на градус». Типовые значения изменяются от 3 % до 5 % оС. Так же, как и бета, альфа зависит от температур, при которых она определяется. Её значение несколько уменьшатся при более высоких температурах.
Под коэффициентом сопротивления подразумевается отношение сопротивления при одной температуре к сопротивлению при другой, более высокой температуре.
Для точных термисторов обычно имеется таблица значений сопротивления (с шагом 1 °С) в зависимости от температуры, которая поставляется изготовителем вместе с другой информацией. Однако иногда удобно иметь точное уравнение при выполнении конструкторских расчетов или (особенно) при использовании ЭВМ для пересчета сопротивления термистора в температуру. Кроме как для очень узких диапазонов температур, экспоненциальное уравнение с одним параметром не удовлетворительно – необходимо большее число параметров.
Наилучшим приближенным выражением, широко используемым в настоящее время, является уравнение Стейнхарта-Харта:
 |
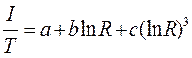Где Т- абсолютная температура (в градусах Кельвина), R – сопротивление термистора; а, b и с –экспериментально полученные константы.
Преобразование уравнения с целью выражения сопротивления в виде функции температуры приводит к довольно громоздкому на вид выражению. Однако, с ним легко обращаться при использовании ЭВМ или программируемого калькулятора:
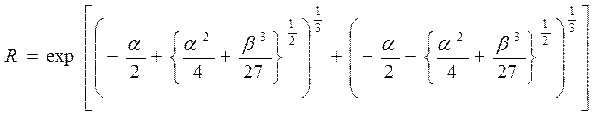
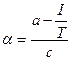
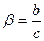Где и.
Необходимо отметить, что данные значения для альфа и бета не относятся к параметрам альфа и бета, используемым в экспоненнциальном уравнении с одним параметром.
Хотя уравнение Стейнхарта-Харта – более сложное, оно, как правило, согласуется с реальными значениями в пределах нескольких тысячных градуса в диапазонах до 1000 оС. Конечно, оно может быть настолько хорошим, если только экспериментальные значения параметров термистора также точны. Температуры с точностью до тысячных градуса можно получить только в первоклассных лабораториях. Скорее пользователь согласится пользоваться паспортными таблицами, чем захочет провести собственные измерения.
Для определения a, b и с необходимо знать точное сопротивление термистора при трёх температурах и подставить каждый набор данных (R и Т) в уравнение Стейнхарта-Харта для определения трех неизвестных. Затем необходимо использовать математические средства для одновременного решения трёх уравнений и получения значений трёх констант. При использовании паспортных таблиц нужно выбирать значения R в зависимости от Т на краях и в середине температурного диапазона, который будет использоваться. Изготовители обычно не указывают паспортные значения для этих констант, так как эти значения изменяются в зависимости от используемого температурного диапазона.
