1) Побудуємо "дерево" (рис. 1.2). Імовірності проставляються за даними п2.
2) Використовуючи дані таблиці 1.2, обчислимо імовірність кожного результату:
р (клієнт позику поверне; фірма рекомендувала) = 735/750 = 0,98;
р (клієнт позику не поверне; фірма рекомендувала) = 15/750 = 0,02;
р (клієнт позику поверне; фірма не рекомендувала) = 225/250 = 0,9;
р (клієнт позику не поверне; фірма не рекомендувала)= 25/250= 0,1.
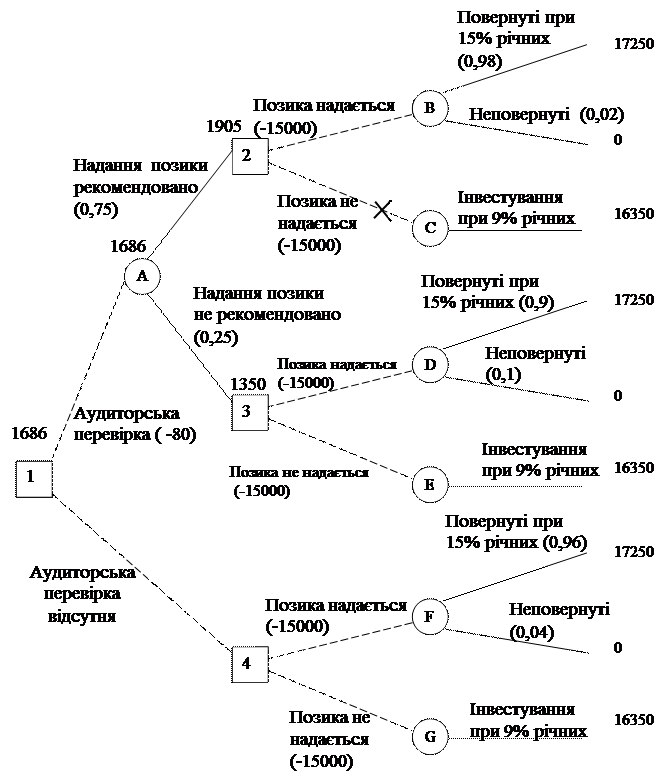
Рисунок 1.2 – Схема дворівневого “дерева” рішень, грн.
3) На цьому етапі зліва направо проставимо грошові результати кожного з "вузлів", використовуючи кінцеві результати, отримані раніше. Будь-які витрати, що зустрічаються, віднімаємо з очікуваних доходів. У такий спосіб розрахуємо все "дерево", опираючись на раніше отримані результати. Після того, як пройдені „квадрати рішень", вибирається "гілка", що веде до найбільшого з можливих, при даному рішенні, очікуваному прибутку. Інша "гілка" закреслюється, а очікуваний прибуток проставляється над „квадратом рішення”.
Спочатку подивимося на „кружки результатів” В і С, що є наслідком „квадрата” 2 (чи видавати позику клієнту?)
Прибуток (П), що очікується від результату В:
П (В) = 17250 грн. ´ 0,98 + 0 ´ 0,02 = 16905 грн.,
чистий прибуток:
ЧП (В) = 16905 - 15000 = 1905 грн.
Прибуток, що очікується від результату С:
П (С) = 16350 грн. ´ 1,0 = 16350 грн.,
чистий прибуток:
ЧП (С) = 16350 - 15000 = 1350 грн.
Припустимо, що ми зараз у „квадраті” 2. Максимальний очікуваний прибуток становить 1905 грн., який знаходиться у „кружку” В. Тому приймаємо рішення видати позику.
Прийнявши рішення, корегуємо "дерево", проставивши чистий очікуваний прибуток у 1905 грн. над „квадратом” 2. "Гілка" – не давати позики – закреслюється, як це показано на рис. 1.2
Те ж саме проводимо з „кружками” наслідків D і Е – результатами рішення 3.
Прибуток, що очікується від результату D:
П (D) = (17250 грн. х 0,9) + (0 х 0,1) = 15525 грн.,
чистий прибуток:
ЧП (D) = 15525 - 15000 = 525 грн.
Аналогічно для результату Е:
П (Е) = 16350 грн. ´ 1,0 = 16350 грн.,
чистий прибуток:
ЧП (Е) = 16350 - 15000 = 1350 грн.
Якби ми були в „квадраті” 3, то максимальний очікуваний прибуток дорівнював би 1350 грн. і можна було б прийняти рішення не видавати позики. Тепер скорегуємо цю частину схеми: над „квадратом” 3 пишемо чистий очікуваний прибуток і приймаємо рішення видати позику.
Нарешті приступаємо до розрахунку „кружків” наслідків F і G які є результатами рішення 4.
П (F) = 17250 ´ 0,96+ 0 ´ 0,04 = 16560 грн.;
ЧП (F) = 16560 - 15000 = 1560 грн.;
П (G) = 16350 ´ 1,0 = 16350 грн.;
ЧП (G) = 16350 - 15000 = 1350 грн.
У „квадраті” 4 максимальний очікуваний чистий прибуток складає 1560 грн., а тому приймаємо рішення видати клієнту позику. Сума 1560 грн. надписується над „квадратом” 4, а альтернативна "гілка" перекреслюється.
Тепер повернемося до „вузлів” А і 1. Використовуючи очікувані чисті прибутки над „квадратами” 2 і 3, розрахуємо математичне очікування для „вузла” А:
П(А) - (1905 грн. ´ 0,75)) + (1350 грн. ´ 0,25) = 1766 грн.
Через те, що аудиторська перевірка коштує 80 грн. очікуваний чистий прибуток становить:
ЧП (A) = 1766 - 80 = 1686 грн.
Тепер можна проставити значення першого рішення „квадрата” 1 (Чи необхідно банку скористатися аудиторською перевіркою?). У цьому „вузлі” максимальне математичне очікування – 1686 грн., а тому перекреслюємо альтернативну „гілку”.
На рис. 1.3 стрілками показана послідовність рішень, що веде до максимального чистого прибутку від „квадрату” 1: за умови використання аудиторської перевірки, якщо видача позики рекомендується аудиторською фірмою, тоді в „квадраті” 2 приймається рішення видати позику, якщо надання позики не рекомендується, то в „квадраті” 3 – не видавати позику, а інвестувати гроші під 9% річні. „Дерево” остаточних рішень для прикладу 1.2 приведено на рис. 1.3.
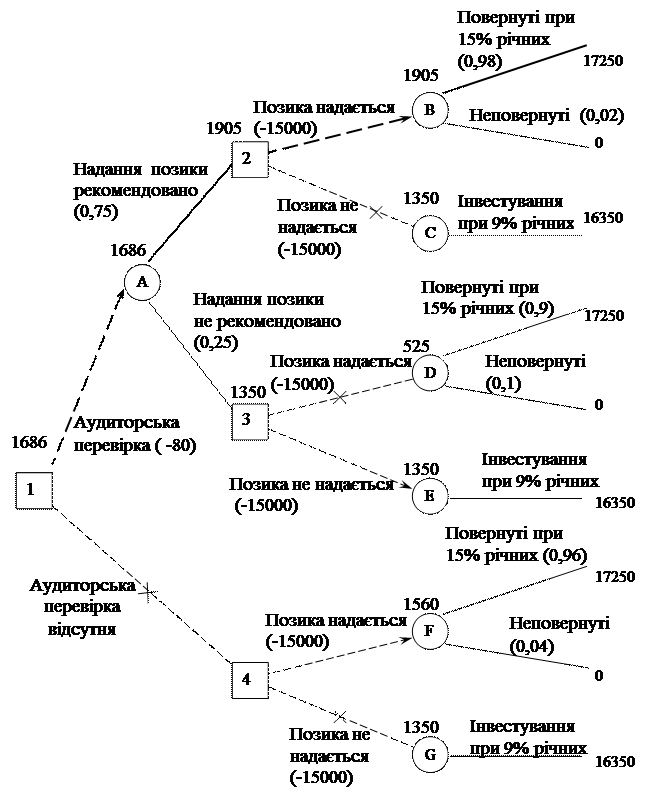
Рисунок 1.3 – Остаточна схема “дерева” рішень прикладу 1.2, грн.
Приклад 1.3 Фірма «КОМ плюс», яка займається дослідженням ринку розраховує розширити свою діяльність, оснастивши персональними комп'ютерами персонал, що займається збиранням даних. Проблема в тому: купувати комп'ютери або орендувати. Спрогнозувати ріст масштабів діяльності фірми в найближчі чотири роки не можна, але можливо розрахувати її значне, середнє і незначне зростання.
Імовірність значного росту масштабу діяльності в перший рік після установки комп'ютерів складає 0,6; середнього і незначного 0,3 і 0,1, відповідно. У наступні три роки ріст може оцінюватися як значний і незначний. Підраховано, якщо ріст значний у перший рік, то імовірність того, що він залишиться таким же і в наступні три роки дорівнює 0,75. Середній ріст першого року зміниться на незначний у наступні роки з імовірністю 0,5; а незначний таким же і залишиться з імовірністю 0,9. Чисті прибутки викликані змінами приведені у табл. 1.3.
Таблиця 1.3 – Чистий прибуток, грн.
| Ріст | Прибуток на кінець року, грн. |
| Значний | |
| Середній | |
| Незначний |
Вартість комп'ютерів — 35000 грн., умови оренди: первісний внесок –15000 грн. плюс 25% чистого наявного виторгу на кінець року. Компанія розраховує одержувати 12% річного прибутку на вкладений капітал.
Для того, щоб вирішити, чи потрібно фірмі купувати або орендувати комп'ютери, скористаємося „деревом”. Критерієм ухвалення рішення є максимізація очікуваного чистого виторгу з обліком 12%-вого збільшення капіталу за рік.






