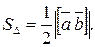Практическая работа № 7
Тема. Вычисление векторного и смешанного произведений.
Цель работы. Проверить знания, умения по вычислению координат и модуля вектора, скалярного, векторного и смешанного произведений векторов.
Теоретический материал.
Векторное произведение
Определение. Три некомпланарных вектора 
взятые в указанном порядке, образуют правую тройку,если с конца третьего вектора 
кратчайший поворот от первого вектора 
ко второму вектору 
виден совершающимся против часовой стрелки, и левую, если по часовой.
Из определения следует, что модуль векторного произведения можно вычислить по формуле:
Если векторы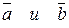 
коллинеарны, то их векторное произведение считается равным нулевому вектору.
Таким образом, для того, чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулевому вектору.
Выражение векторного произведения через координаты
Пусть заданы два вектора
Найдём векторное произведение этих векторов по следующей формуле:
Данную формулу можно записать иначе:
И, значит,
