Примеры решения задач

Задача 1. Для заданной схемы механизма и следующих исходных данных: w_ОА =4 с^-1; e_ОА =4 с^-2;ОА = r =0,5 м; АВ = 2r; ВС = rÖ2; Ð ОАВ = 90°; Ð АВС = 45°, определить ускорение точки В.. Задачу решить двумя способами (при решении использовать результаты, полученные в подобной задаче на предыдущем занятии).

Первый способ.

1. Определяем ускорение полюса точки А:

,

м/с²,

м/с².

2. Определяем центростремительное ускорение звена АВ:

м/с².

3. Определяем центростремительное ускорение точки В в ее вращательном движении относительно точки С:

.

4. В данный задаче ускорение точки В можно определить путем решения системы векторных уравнений:

(12)

Необходимость решения системы уравнений связана с тем, что во-первых, угловое ускорение звена АВ e_АВ невозможно в данном случае определить аналитически, (т. е. невозможно определить модуль вращательного ускорения звена АВ ), а во-вторых, не известно направление ускорения точки В.

Построение начинаем с первого уравнения системы (12). В точке В (рис.22) последовательно откладываем нормальное и тангенциальное ускорение полюса точки А, затем параллельно звену АВ по направлению от точки В к полюсу А откладываем центростремительное ускорение звена АВ и перпендикулярно к нему проводим прямую (I - I), на которой будет лежать вращательное ускорение звена АВ . Так как модуль этого вектора неизвестен, переходим ко второму уравнению системы (12) и из точки В откладываем нормальное ускорение . Перпендикулярно к нему проводим прямую (II - II), которая при пересечении с прямой (I - I) дает конец вектора ускорения точки В. Таким образом, на прямой (I - I) получаем вектор , а на прямой (II - II) – вектор , тогда вектор, проведенный из точки В в точку пересечения прямых (I - I) и (II - II) будет вектором ускорения точки В. Измерив длину вектора а_В, и переведя ее в масштабе, получим значение модуля вектора, равное 11,7 м/с².

Измеряем длину вектора м/с ² и определяем угловое ускорение звена АВ:

с ^-2.

Чтобы решить задачу аналитически, проецируем оба векторных уравнения системы (12), на оси Вx (проведена по звену АВ) и Вy (проведена перпендикулярно к звену АВ). После проецирования получим систему из 4-х уравнений, которая позволит найти 4 неизвестные величины: , , , 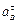. (13)

 

Рис. 22

 

Из уравнения (13) находим а _Вх и подставляем в уравнение (15), откуда получаем :

м/с ²,

м/с ².

Затем определяем а_Ву из уравнения (16):

м/с ².

Находим из уравнения (14):

м/с ².

И угловое ускорение звена АВ:

с ^-2.

Модуль ускорения точки В можно оценить как корень квадратный из суммы квадратов проекций:

м/с².

Сравнение аналитического и графического способов решения задачи показывают, что разница в полученных значениях не превышает 5%.

Второй способ решения задачи можно показать для точки Д, середины звена АВ. При этом воспользуемся результатами решения задачи при определении ускорения точки В. Этот случай рассмотрен на стр. 15 (рис.14). Построим в точке В параллелограмм ускорений по уравнению:

.

Определим угол как угол между направлением ускорения звена АВ и самим звеном. Отложим этот угол от векторов ускорений точек А и В, и на пересечении этих лучей определим положение точки Q – мгновенного центра ускорений звена АВ (см. рис. 23). Ускорение точки Д отложим под углом к линии QД.

 

Задача 2. Цилиндр радиусом r = 40 см катится по плоскости без скольжения. Скорость и ускорение точек его оси в данный момент:

v_C = 0,4 м/с, a_C = 0,2 м/с². Диск радиусом R = 50 см жестко соединен с цилиндром в сечении, где плоскость не препятствует его движению. Определить в данный момент времени ускорения концов двух диаметров диска в точках А, В, Д, Е. Определить также положение мгновенного центра ускорений диска (рис. 24).

 

Рис. 23

Решение. По условию данной задачи можно определить аналитически угловую скорость и угловое ускорение диска. Поэтому для определения ускорений точек А, В, Д, Е диска можно применить два способа решения (см. стр. 11 и 12).

Сначала определяем ω и ε. Мгновенный центр скоростей диска Р находится в точке соприкосновения поперечного сечения цилиндра с неподвижной плоскостью (рис. 25).

Модуль угловой скорости диска определяем как отношение скорости полюса к расстоянию от полюса до МЦС:

.

Расстояние от центра диска С до МЦС точки Р при движении не изменяется, а потому угловое ускорение можно определить как производную от угловой скорости:

.

Подставляя в это выражение числовые значения, находим модуль:

.

Так как вращение диска ускоренное, то имеет такое же направление как и (рис. 25).

Первый способ. Принимаем за полюс центр диска С, ускорение которого известно, и определяем ускорения точек А,В,Д,Е по формуле (4):

.

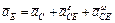
Модули вращательного ускорения точек относительно полюса точки С будут равны:

= = = .

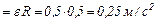Модули центростремительного ускорения точе к относительно полюса точки С будут равны:

= = = .

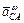Откладываем (рис. 25) в каждой точке векторы ускорения полюса точки С, векторы вращательного ускорения точек относительно полюса (направляем перпендикулярно к отрезкам, соединяющим точку и полюс по направлению ε) и центростремительного ускорения точек относительно полюса (направляем от каждой точки к полюсу – точке С).

Ускорение каждой точки определяется диагональю прямоугольника, сторонами которого являются сумма двух векторов, оказавшихся на одной прямой, и третий вектор, перпендикулярный к ним:

;

;

;

.

Второй способ. Приняв точку С за полюс, находим угол a и расстояние СQ по (9) и (10) соответственно;

;

;

.

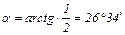Откладываем угол a от ускорения по направлению , т. е. по направлению вращения часовой стрелки. На построенной полупрямой откладываем отрезок СQ и получаем мгновенный центр ускорений (МЦУ) Q (рис. 26).

Если соединить точки А,В,Д,Е с точкой Q, то ускорения этих точек составят с отрезками QА, QB, QД, QE один и тот же угол a = 26°34¢. Направление отсчета угла a от ускорения точки к отрезкам, соединяющим точку и МЦУ, совпадает с направлением . Модули ускорений точек пропорциональны расстояниямот точек до МЦУ, что видно по рис. 26, на котором ускорения точек А,В,Д,Е и С отложены в масштабе, по их истинным направлениям. Определив отрезки QА, QB, QД, QE, можно было бы вычислить ускорения точек по формуле (показано на примере для точки А)

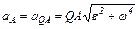
но в рассмотренном примере этот способ решения требует больших вычислений, чем выполненное решение.

Необходимо отметить, что при определении ускорений точек плоской фигуры пользоваться мгновенным центром ускорений целесообразно только в том, случае, когда положение мгновенного центра ускорений находится легко, т. е. тогда, когда его применение приводит к упрощению (рис. 26), а не к усложнению вычислений.