4.1.1. Понятие «метод»
Метод (греч. methodos — путь, способ исследование, обучения, изложения) —это:
1) система правил и приемов подхода к изучению явлений и закономерностей природы, общества и мышления;
2) путь, способ достижения определенных результатов в познании и практике;
3) прием теоретического исследования или практического осуществления чего-нибудь, исходящий из знания закономерностей развития объективной действительности и исследуемого предмета, явления, процесса [12].
Основное содержание метода науки образуют прежде всего научные теории, проверенные практикой: любая такая теория по существу выступает в функции метода при построении других теорий в данной или даже в иных областях знания или в функции метода, определяющего содержание и последовательность экспериментальной деятельности. Поэтому различие между методом и теорией носит функциональный характер: формируясь в качестве теоретического результата прошлого исследования, метод выступает как исходный пункт и условие последующих исследований.
Хотя проблема метода обсуждалась уже в античной философии (которая впервые обратила внимание на взаимозависимость результата и метода познания), систематическое развитие методов познания и их изучение начинаются лишь в новое время, с возникновением экспериментальной науки: именно эксперимент потребовал строгих методов, дающих однозначный результат. С этого времени развитие, совершенствование метода выступает как важнейшая составная часть всего прогресса науки.
Классификация методов науки весьма разнообразна, как и сама наука. Существует множество различных классификаций метода. Современную систему методов науки можно представить в следующем виде (табл. 4.1.).
Знание метода имеет огромное практическое и эвристическое значение, так как оно ориентирует исследователя, помогает ему выбрать существенное и отчленить второстепенное, наметить путь восхождения от известного к неизвестному, от простого к сложному, от единичного к частному и общему, от исходных посылок к универсальному и т. д.
Таблица 4.1. Классификация методов научного знания
| № | Критерий | Методы |
| Эксперимент | Метод эксперимента, метод обработки эмпирических или экспериментальных данных | |
| Направленность | Философские и специально-научные. Построение научных теорий, их проверка | |
| Изложение научных результатов | Метод членения, основанный на различных стадиях исследований | |
| Форма, смысл, конкретизация | Количественные и качественные, аналитические, модерирование | |
| Формальности | Детерминированные и вероятностные | |
| Характер метода | Сравнение, анализ и синтез, идеализация, обобщение, индукция и дедукция | |
| Принадлежность к научному знанию | Физические, химические, биологические, механические, астрономические и т.д. |
Важная особенность современного этапа развития науки заключается в существ, возрастании роли конструктивных моментов в науч. познании: характер задач современной науки таков, что она всё чаще не просто отражает те или иные аспекты реальности, но и проектирует реальность в соответствии с определёнными целями. Это ведёт к необходимости осуществлять широкое конструирование методов познания, особенно формальных, в частности математических методов. Соответственно расширяется и специальное изучение логической структуры формальных методов. Одним из конкретных выражений усиления конструктивности познания является быстро растущее распространение М. моделирования, который вообще может служить ярким примером подлинно эвристической роли метода познания.
Повышение уровня абстрактности современной науки выдвинуло важную проблему интерпретации результатов исследований, особенно исследования, выполненного с широким применением средств формализации, а также с привлечением огромного количества методов моделирования.
Развитие современной науки и дифференциации мышления характеризуется столь широким многообразием методов познания, что привело к учению о методах – методологии [43,44].
4.1.2. Понятие «теория», «парадигма», «идея», «концепция» и «принцип»
Теория (греч. theoria – наблюдение, исследование, рассматривание), в широком смысле — комплекс взглядов, представлений, идей, направленных на истолкование и объяснение каких-либо явлений, процессов; в более узком и специальном смысле — высшая, самая развитая форма организации научного знания, дающая целостное представление о закономерностях и существенных связях определенной области действительности — объекта данной теории.
По своему строению теория представляет внутренне дифференцированную, но целостную систему знания, которую характеризуют логическая зависимость одних элементов от других, выводимость содержания теории из некоторой совокупности утверждений и понятий — исходного базиса теории — по определённым логико-методологическим принципам и правилам.
Как форма научного знания теория выступает, с одной стороны, как наиболее сложная и развитая форма научного знаниях. Другие его формы научного знания такие, как законы науки, классификации, типологии, первичные объяснительные схемы — генетически могут предшествовать собственно теории, составляя базу её формирования. С другой стороны, они нередко сосуществуют с теорией, взаимодействуя с нею в системе науки, и даже входят в теорию в качестве её элементов (теоретические законы, типологии, основанные на теории).
Научное знание вообще теоретично с самого начала, т.е. всегда связано с размышлением о содержании понятий и о той исследовательской деятельности, которая к нему приводит. При этом, однако, формы и глубина теоретического мышления могут сильно варьировать, что находит историческое выражение в развитии структуры теоретического знания, в формировании различных способов его внутренней организации. Если теоретическое мышление вообще (теория в широком смысле слова) необходимо сопутствует всякой науке, то теория в собственном, более строгом смысле появляется на достаточно высоких этапах развития науки.
Переход от эмпирической стадии науки: эмпирика (от греч. empiria – опыт), которая ограничивается классификацией и обобщением опытных данных, к теоретической стадии, когда появляются и развиваются теории в собственном смысле, осуществляется через ряд промежуточных форм теоретизации, в рамках которых формируются первичные теоретические конструкции. Будучи источником возникновения теории, сами эти конструкции, однако, ещё не образуют теории: её возникновение связано с возможностью построения многоуровневых конструкций, которые развиваются, конкретизируются и внутренне дифференцируются в процессе деятельности теоретического мышления.
В этом смысле зрелая теория представляет собой не просто сумму связанных между собой знаний, но и содержит определённый механизм построения знания, развёртывания теоретического содержания, воплощает некоторую программу исследования; всё это и создаёт целостность теории как единой системы знания. Подобная возможность развития аппарата научных абстракций в рамках и на основе теории делает последнюю мощнейшим средством решения фундаментальных задач познания действительности.
В современной методологии науки принято выделять следующие основные компоненты теории:
1) исходная эмпирическая основа, которая включает множество зафиксированных в данной области знания фактов, достигнутых в ходе экспериментов и требующих теоретического объяснения;
2) исходная теоретическая основа — множество первичных допущений, постулатов, аксиом, общих законов теории, в совокупности описывающих идеализированный объект теории;
3) логика теории— множество допустимых в рамках теории правил логического вывода и доказательства;
4) совокупность выведенных в теории утверждений с их доказательствами, составляющую основной массив теоретического знания.
Методологически центральную роль в формировании теории играет лежащий в её основе идеализированный объект — теоретическая модель существенных, связей реальности, представленных с помощью определённых гипотетических допущений и идеализаций. Построение идеализированного объекта теории— необходимый этап создания любой теории, осуществляемый в специфических для разных областей знания формах. Примеры идеализированных объектов теории:
1) в классической механике - система материальных точек;
2) в молекулярно-кинетической теории — множество замкнутых в определённом объёме хаотически соударяющихся молекул, представляемых в виде абсолютно упругих материальных точек;
3) в кибернетике – виды управления;
4) в теории надёжности – множество элементов, находящихся в различных состояниях;
5) в теории стоимости – структура производства как теоретическая модель способа производства.
Многообразию форм идеализации и соответственно типов идеализированных объектов соответствует и многообразие видов теорий. В теории описательного типа, решающей главным образом задачи описания и упорядочения обычно весьма обширного эмпирического материала, построение идеализированного объекта фактически сводится к вычленению исходной схемы понятий. В современных математизированных теориях идеализированный объект выступает обычно в виде математической модели или совокупности таких моделей. В дедуктивных теоретических системах построение идеализированного объекта по существу совпадает с построением исходного теоретического базиса.
Процесс развёртывания содержания теории предполагает максимальное выявление возможностей, заложенных в исходных посылках теории, в структуре её идеализированного объекта. В частности, в теориях, использующих математический формализм, развёртывание содержания предполагает формальные операции со знаками математизированного языка, выражающего те или иные параметры объекта. В теориях в которых математический формализм не применяется или недостаточно развит, на первый план выдвигаются рассуждения, опирающиеся на анализ содержания исходных посылок теории, на мысленный эксперимент с идеализированными объектами. Наряду с этим развёртывание теории предполагает построение новых уровней и слоёв содержания теории на основе конкретизации теоретического знания о реальном предмете. Это связано с включением в состав теории новых допущений, с построением более содержательных идеализированных объектов [44].
Парадигма (от греч. — пример, образец) – это:
1) понятие, используемое в античной и средневековой философии для характеристики взаимоотношения духовного и реального мира;
2) теория (или модель постановки проблем), принятая в качестве образца решения исследовательских задач.
Платон усматривал в идеях реально существующие прообразы вещей, их идеальные образцы, обладающие подлинным существованием: «демиург создаёт всё существующее, взирая на неизменно сущее как на образец, или первообраз» («Тимей»). Эта линия в трактовке идеи как парадигмы, образца, нашла своё продолжение в неоплатонизме, в рамках которого выдвигались различные толкования соотношения демиурга, образца и идей; в средневековой философии она выразилась в учении об эманации бога, в творении им мира по своему образу и подобию.
Демиург (греч. δημιουργός, буквально — изготавливающий вещи для народа, отсюда — ремесленник, мастер, от δῆμος — народ и ἔργον — работа), термин др.-греч. философии для обозначения «творца» («мастера»), введённый в философский лексикон Платоном в «Тимее». Демиург — «творец и отец этой Вселенной», создатель низших богов, мировой души и бессмертной части человеческой души, творит космос из со-вечной ему материи («кормилицы», «восприемницы», «пластической массы»), наделённой вечным беспорядочным движением, взирая на вечный первообраз-парадигму — эйдос (28а, 29а). В этом его отличие от бога теистических религий, творящего мир из ничего: ни материя, ни первообраз от Демиурга не зависят. Кроме того, он не всесилен: стремлению ума-Демиург устроить всё «как можно лучше» противостоит сопротивление материи в виде детерминистической «необходимости» (ананке). Демиург «Тимея», очевидно, тождествен с «причиной соединения» предела и беспредельного (формы и материи)— прообразом «действующей причины» Аристотеля в платоновском «Филебе». Характерное замечание Платона о «правдоподобном мифе» «Тимей» дало повод уже в Древней Академии истолковать космогонию «Тимея» как условно-метафорический язык, применяемый в «дидактических целях» для выражения вневременных онтологических структур. Аристотель подчёркнуто игнорировал Демиурга «Тимея» при изложении платоновского учения и употреблял термин «Демиург» только в прямом значении «ремесленник, мастер»; единственное возможное исключение — ранний диалог «О философии». Трансцендентное понимание высшего божественного, принципа в позднем платонизме приводит к перекладыванию функций Демиурга (непосредственно контактирующего с материей в акте творения) на вторичного бога-посредника, эманирующего из первопринципа.
Эманация (от лат. emanation – истечение, распространение), философское понятие, специально разработанное в неоплатонизме, означающее переход от высшей и совершенной онтологической ступени универсума к менее совершенным и низким ступеням. Как тип развития эманация – нисхождение противоположна восхождению, совершенствованию
Неоплатонизм – это последний этап античного платонизма. Основателем неоплатонизма обычно считают Плотина (III в.) или его учителя Аммония. Неоплатонизм замыкает средний платонизм, вбирает в себя неопифагореизм и использует амстатеизм в качестве введения – главным образом логического – учение Платона. Основные понятиия неоплатонизма: во главе иерархии бытия стоит сверхсущее единое – благо, постижимое только в сверхумном экстазе и выразимое только средствами отрицательной теологии. Далее в порядке нисхождения (эманации) из единого следовали бытие – ум (нус) с идеями в нём, душа, обращённое к уму и к чувственному космосу, вечному в своём временном бытии.
В немецком классическом идеализме учение о парадигме развёртывается в плане анализа принципов внешнего и внутреннего единства различных формообразований, в учении о первообразе или прообразе системной организации всех тел. Согласно Ф. Шеллингу и Г. Гегелю, принципы упорядочивания и целостной организации природных тел характеризует духовный, идеальный прообраз.
В философии науки понятие «парадигма» было введено позитивистом Г. Бергманом для характеристики нормативности методологии, однако широкое распространение оно приобрело после работ американского историка физики Т. Куна. Стремясь построить теорию научных революций, Т. Кун предложил систему понятий, среди которых важное место принадлежит понятию парадигмы, т. е. «... признанным всеми научным достижениям, которые в течение определенного времени дают модель постановки проблем и их решений научному сообществу». Смена парадигмы представляет собой научную революцию. Трактовка Т. Куном понятия «парадигмы» вызвала дискуссию, в ходе которой отмечалась неоднозначность этого понятия (К. Поппер, И. Лакатос, М. Мастерман и др.). Неоднозначность понятия парадигмы, под которым у Куна понимается и теория, признанная научным сообществом, и правила и стандарты научной практики, и стандартная система методов, потребовала от него пересмотра и конкретизации этого понятия, что было осуществлено в понятии «дисциплинарная матрица» и её компонентов (символического обобщения, метафизической части парадигмы, ценности и собственно образцы решения исследовательских задач). Вместе с тем понятие парадигмы используется в теории и истории науки для характеристики формирования научной дисциплины, описания различных этапов научного знания (допарадигмального, т. е. периода, когда не существует теория, признанная научным сообществом, и парадигмального), для анализа научных революций.
В марксистской литературе понятие парадигмы используется при анализе процессов художественного и научного творчества (художеств, канонов, стилей в искусстве и стилей мысли в науке и пр.). К. Маркс и Ф. Энгельс обратили внимание на то, что различные науки принимались в качестве образцов и выдвигались на первый план в концепциях науки: если Ф. Бэкон видел в качественной физике основу естественных наук, то Гоббс провозглашал геометрию «главной наукой». А. Грамши, критикуя позитивистский сциентизм, отмечал, что длительное время наука отождествлялась с естественными науками. «Экспериментальные и естественные науки являлись в определенную эпоху „моделью", „образцом"; и поскольку общественные науки (политика и история) стремились найти объективную основу, которая в научном отношении была бы пригодной для того, чтобы придать им такую же точность и силу, какими обладали естественные науки, то понятно, что к этим последним обращались при создании языка общественных наук» [7]. Признавая общие принципы деятельности учёных, определённые культурные стандарты, эталоны и методологические регулятивы, выступающие в качестве образцов при решении исследовательских задач внутри отдельной научной дисциплины, Марксистская методология науки отвергает унификацию реального методологического и предметного многообразия научных дисциплин, попытки построения некоторой нормативной методологии науки [44].
Идея (греч. idea – вид, образ) – это:
1) высшая ступень в развитии понятия, присущая только человеческому мозгу;
2) форма постижения в мысли явлений объективной реальности, включающая в себя сознание цели и проекции дальнейшего познания и практического преобразования мира. Так как познание есть отражение действительности, то идея – это специфическая форма этого отражения. Понятие «идея» было выдвинуто ещё в античности. Демокрит: «идеи – это неделимые умопостигаемые формы, атомы». Платон: «идеи— это идеальная сущность, лишённая телесности и являющаяся подлинно объективной реальностью, находящейся вне конкретных вещей и явлений». Идеи составляют особый идеальный мир. В средние века идеи понимались как прообраз вещей, принадлежащий божественному духу; бог творил вещи согласно своим идеям, идеальным формам. В новое время, в XVII—XVIII вв., на первый план выдвигается теоретико-познавательный аспект идеи — разрабатывается учение об идее как способе человеческого познания, ставится вопрос о происхождении идей, их познавательной ценности и отношении к объективному миру. Эмпиризм связывал идеи с ощущениями и восприятиями людей, а рационализм — со спонтанной деятельностью мышления.
Большое место учение об идеи занимало в немецком классическом идеализме: И. Кант называл идеями понятия разума, которым нет соответствующего предмета в нашей чувственности; по Фихте, идеи — это имманентные цели, согласно которым «Я» творит мир; для Г. Гегеля идея является объективной истиной, совпадением субъекта и объекта, венчающим весь процесс развития.
В марксистской концепции исходным является материалистический тезис о познании как отражении действительности, об идее как специфической форме этого отражения. Ф. Энгельс: «Все идеи извлечены из опыта, они — отражения действительности, верные или искаженные» [48]. Однако идея не сводится к фиксации результатов опыта, но является отражением вещи, свойства или отношения не просто в их наличном бытии, а в необходимости и возможности, в тенденции развития. В. И. Ленин: «Идея как высшая форма теоретического освоения действительности» [22]. В идее происходит, наиболее полное совпадение содержания мысли с объективной реальностью, это — объективное и конкретное, всестороннее знание действительности, которое готово для своего практического воплощения. Отражение объективной реальности и постановка практической цели перед человеком, находящиеся в органическом единстве, определяют специфику идеи и её место в движении человеческого сознания.
Таким образом, идея является активным, посредствующим звеном в развитии действительности, в процессе практической деятельности человека, создающей новые, ранее не существовавшие формы реальности.
В науке идеи выполняют различную роль. Они не только подытоживают опыт предшествующего развития знания в той или иной области, но служат основой, синтезирующей знание в некую целостную систему, выполняют роль активных эвристических принципов объяснения явлений, поисков новых путей решения проблем [44].
Концепция (лат. conception – понимание, система) – это:
1) система взаимосвязанных и вытекающих один из другого взлётов на те или иные явления, процессы;
2) способ понимания, трактовки каких-либо явлений, событий;
3) основополагающая идея какой-либо теории;
4) общий замысел, главная мысль научного труда
Примеры концепции: природный и техногенный риск [32].
Припцип (лат. principium) – основополагающее первоначало, основное положение, исходный пункт, предпосылка какой-либо теории, концепции. В это понятие часто вкладывают смысл: убеждение, взгляд, точка зрения, основная особенность в устройстве чего-либо [29].
Пример: принцип соответствия – любая новая теория должна содержать в себе предыдущую в качестве частного случая. Так, все формулы специальной теории относительности при малых скоростях переходят в формулы ньютоновской механики [12].
4.1.3. Понятия «модель», «закон», «аксиома» и «постулат»
Модель (лат. modus — мера, франц. modele — образец) — искусственно созданный объект в виде схемы, чертежа, логико-математических знаковых формул, физической конструкции и т. п., который, «будучи аналогичен (подобен, сходен) исследуемому объекту (плотине, кораблю, самолету, ракете, космической станции и т. п.). Модель отображает и воспроизводит в более простом, уменьшенном виде структуру, свойства, взаимосвязи и отношения между элементами исследуемого объекта, непосредственное изучение которого связано с какими-либо трудностями, большими затратами средств и энергии или просто недоступно. Тем самым модель облегчает процесс получения информации об интересующем нас предмете. Исследуемый объект, по отношению к которому изготавливается модель, называется оригиналом, образцом, прототипом [12].
Таким образом модель является аналогом для хранения и расширения знания (информации) об оригинале, конструирования оригинала, преобразования и управления им. С гносеологической точки зрения модель — это «представитель», «заместитель» оригинала в познании и практике. Результаты разработки и исследования модели при определённых условиях, выясняемых в логике и методологии и специфических для различных областей и типов моделей, распространяются на оригинал. С логической точки зрения подобное распространение основано на отношениях изоморфизма и гомоморфизма, существующих между моделью и тем, что с её помощью моделируется.
Напомним, что изоморфизм и гомоморфизм – это логико-математические понятия, выражающие одинаковость (изоморфизм; от греч. isos - одинаковый, равный, подобный и morphe – вид, форма) либо уподобление (гомоморфизм; от греч. homos – один и тот же, равный) строение (структуры) систем (множеств, процессов, конструкций. Системы А и А’ называются изоморфными (или находящимися в отношении изоморфизма), если между их элементами, также функциями (операциями), свойствами и отношениями, осмысленными для этих систем, существует или может быть установлено взаимно-однозначное соответствие [44].
В настоящее время в науке при оперирования термином «модель» сложилась следующая ситуация. В таких науках, как физика, космология, математическая лингвистика, математическая экономика, кибернетика, под термином «модель» понимаются системы математических утверждений (аксиом, уравнений), служащие для описания некоторой области реальных либо абстрактных объектов. В то же самое время как в логике и математике термин «модель» имеет иной смысл. Под моделью здесь понимается интерпретация систем логико-математических положений. Изучение таких интерпретаций производится в логической семантике, а также в теории моделей математической логики, где под «моделью» понимают произвольное множество элементов с определёнными на нём функциями и предикатами. Однако независимо от того, какой член отношения аналог — оригинал рассматривается в качестве модели, последняя всегда выполняет познавательную роль, выступая средством объяснения, предсказания и эвристики. В теории систем под моделью системы понимается описание систем, отображающее определенную группу её свойств [32].
Классификация моделей. С развитием математической логики, кибернетики и теории систем укрепилась следующая классификация моделей (рис. 4.2.) [32,39].
В основе моделирования лежит теория подобия, которая утверждает, что абсолютное подобие может иметь место лишь при замене одного объекта другим точно таким же. При моделировании абсолютное подобие не имеет места и стремятся к тому, чтобы модель достаточно хорошо отображала исследуемую сторону функционирования объекта.
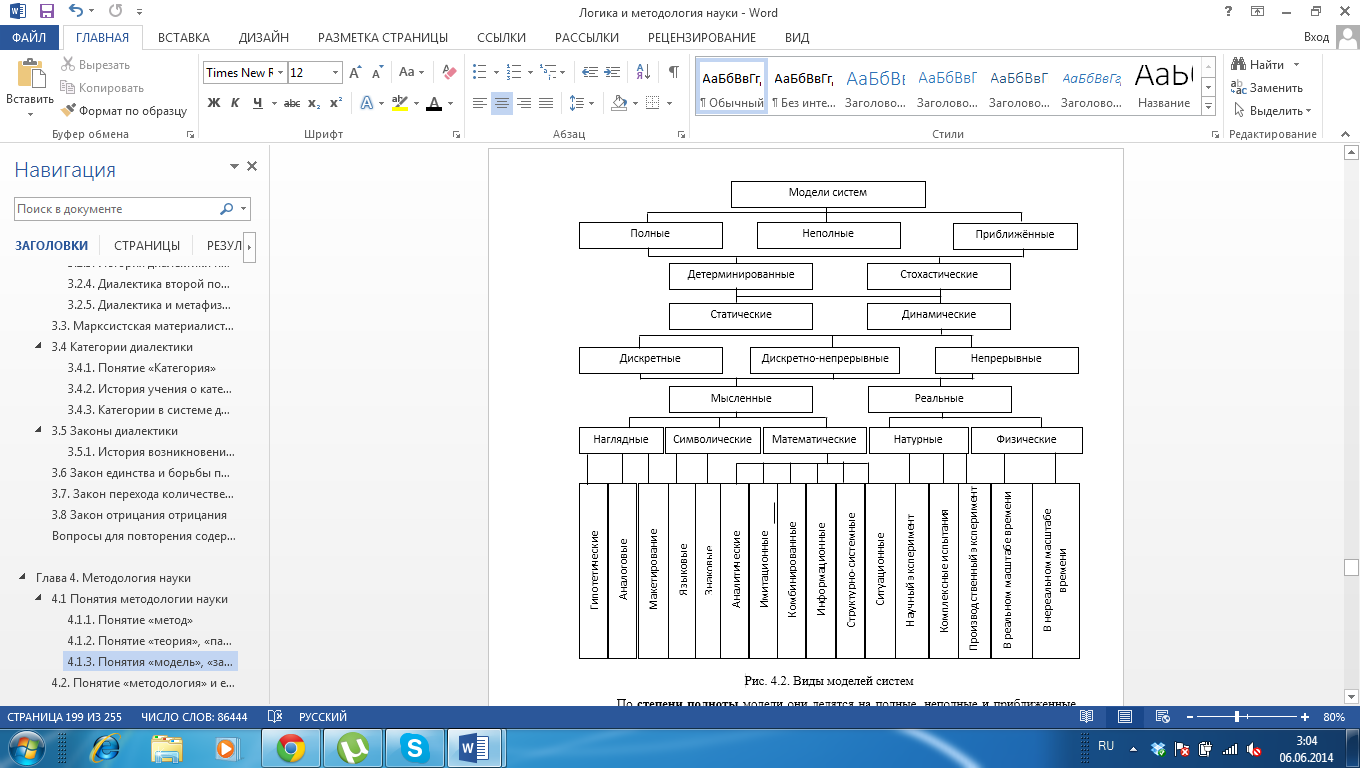
Рис. 4.2. Виды моделей систем
По степени полноты модели они делятся на полные, неполные и приближенные. Полные модели идентичны объекту во времени и пространстве. Для неполных моделей эта идентичность не сохраняется. В основе приближённых моделей лежит подобие, при котором некоторые стороны функционирования реального объекта не моделируются совсем.
В зависимости от характера изучаемых процессов в системе модели подразделяются на детерминированные и стохастические, статические и динамические, дискретные, непрерывные и дискретно-непрерывные. Детерминированные модели отображают процессы, в которых предполагается отсутствие случайных воздействий. Стохастические модели учитывают вероятностные процессы и события. Статистические модели служат для описания поведения объекта в фиксированный момент времени, а динамические – для исследования объекта во времени. Дискретные, непрерывные и дискретно-непрерывные модели используются для описания процессов, имеющих изменение во времени. При этом оперируют аналоговыми, цифровыми, аналого-цифровыми моделями.
В зависимости от формы представления объекта модели классифицируются на мысленные и реальные. Мысленное моделирование применяется тогда, когда модели не реализуемы в заданном интервале времени либо отсутствуют условия для их физического создания (например, ситуации в микромире)
Мысленное моделирование реализуется в виде наглядного, символического и математического. Создаются наглядные модели на базе представлений человека о реальных объектах, отображающих явления и процессы, протекающие в объекте. В основу гипотетических моделей закладывается гипотеза о закономерностях протекания процесса в реальном объекта, которая отражает уровень знаний исследователя об объекте и базируется на причинно-следственных связях между входом и выходом изучаемого объекта. Этот вид моделей используется, когда знаний об объекте недостаточно для построения формальных моделей. Аналоговые модели основаны на применении аналогий различных уровней. Для достаточно простых объектов наивысшим уровнем является полная аналогия. С усложнением системы используются аналогии последующих уровней, когда аналоговая модель отображает несколько либо только одну сторону функционирования объекта. Макетирование применяется, когда протекающие в реальном объекте процессы не поддаются физическому моделированию либо могут предшествовать проведении других видов моделирования. В основе построения мысленных моделей макетов также лежат аналогии, обычно базирующиеся на причинно-следственных связях между явлениями и процессами в объекте.
Символические модели представляют собой искусственный процесс создания логического объекта, который замещает реальный и выражает основные свойства его отношений с помощью определенной системы знаков и символов. В основе языкового моделирования служит некоторый тезаурус, который образуется из набора входящих понятий, причём этот набор должен быть фиксированным. Между тезаурусом и обычным словарем имеются принципиальные различия. Тезаурус – словарь, который очищен от неоднозначности, т.е. в нем каждому слову может соответствовать лишь единственное понятие, хотя в обычном словаре одному слову может соответствовать несколько понятий, т.е. знаки, а также определенные операции между этими знаками, то можно реализовать знаковое моделирование и с помощью знаков отображать набор понятий – составлять отдельные цепочки из слов и предложений. Используя операции объединения, пересечения и дополнения теории множеств, можно в отдельных символах дать описание какого-то реального объекта.
Математические модели – устанавливают соответствие данному реальному объекту некоторого математического объекта, называемого математической моделью. В принципе, для исследования характеристик процесса функционирования любой системы математическими методами, включая и машинные, должна быть обязательно проведена формализация этого процесса, т.е. построена математическая модель. Исследование математической модели позволяет получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и от задач исследования объекта, требуемой достоверности и точности решения задачи. Любая математическая модель, как и всякая другая, описывает реальный объект с некоторой степенью приближения. Для аналитического моделирования характерно то, что процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (алгебраических, интегродифференциальных, конечноразностных и т.д.) или логических условий. Аналитическая модель исследуется следующими методами: аналитическим, когда стремятся получить в общем виде явные зависимости, связывающие искомые характеристики с начальными условиями, параметрами и переменными системы; численным, когда, не умея решать уравнений в общем виде, стремятся получить числовые результаты при конкретных начальных данных; качественным, когда, не имея решения в явном виде, можно найти некоторые свойства решения (например, оценить устойчивость решения).
В настоящее время распространены методы машинной реализации исследования характеристик процесс функционирования сложных систем. Для реализации математической модели на ЭВМ необходимо построить соответствующий моделирующий алгоритм.
Имитационные модели реализуют алгоритм, который воспроизводит процесс функционирования системы во времени, причём имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени, что позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени, дающие возможность оценить характеристики системы. Основным преимуществом имитационных моделей по сравнению с аналитическими является возможность решения более сложных задач. Имитационные модели позволяют достаточно просто учитывать такие факторы, как наличие дискретных и непрерывных элементов, нелинейные характеристики элементов системы, многочисленные случайные воздействия и др., которые часто создают трудности при аналитических исследованиях. В настоящее время имитационные модели – наиболее эффективный метод исследования сложных систем, а часто и единственный практически доступный метод получения информации о поведении системы, особенно на этапе ее проектирования.
Имитационные модели используют метод статистического моделирования и метод статистических испытаний (Монте-Карло). Если результаты, полученные при воспроизведении на имитационной модели, являются реализациями случайных величин и функций, тогда для нахождения характеристик процесса требуется его многократное воспроизведение с последующей обработкой информации. Поэтому целесообразно в качестве метода машинной реализации имитационной модели использовать метод статического моделирования. Первоначально был разработан метод статических испытаний, представляющий собой численный метод, который применялся для моделирования случайных величин и функций, вероятностные характеристики которых совпадали с решениями аналитических задач (такая процедура получила название Монте-Карло). Затем этот приём стали применять и для машинной имитации с целью исследования характеристик процессов функционирования систем, подверженных случайным воздействиям, т.е. появился метод статического моделирования.
Метод имитационного моделирования применяется для оценки вариантов структуры системы, эффективности различных алгоритмов управления системой, влияния изменения различных параметров системы. Имитационные модели могут быть положены в основу структурного, алгоритмического и параметрического синтеза больших систем, когда требуется создать систему с заданными характеристиками при определенных ограничениях. Система должны быть оптимальной по некотрым критериям эффективности.
Комбинированные (аналитико-имитационные) модели позволяют объединить достоинства аналитических и имитационных моделей. При построении комбинированных моделей производится предварительная декомпозиция процесса функционирования объекта на составляющие подпроцессы, и для тех из них, где это возможно, используются аналитические модели, а для остальных подпроцессов строятся имитационные модели. Такой подход позволяет охватить качественно новые классы систем, которые не могут быть исследованы с использованием аналитических и имитационных моделей в отдельности
Информационные модели (часто называемые кибернетическими) связаны с исследованиями моделей, в которых отсутствует непосредственное подобие физических процессов, происходящих в моделях, реальным процессам. В этом случае стремятся отобразить лишь некоторую функцию и рассматривают реальный объект как «чёрный ящик», имеющий ряд входов и выходов, и моделируются некоторые связи между выходами и входами. Таким образом, в основе информационных (кибернетических) моделей лежит отражение некоторых информационных процессов управления, что позволяет оценить поведение реального объекта. Для построения модели в этом случае необходимо выделить исследуемую функцию реального объекта, попытаться формализовать эту функцию в виде некоторых операторов связи между входом и выходом и воспроизвести данную функцию на имитационной модели, причем на совершенно другом математическом языке и, естественно, иной физической реализации процесса.
Структурно-системные модели базируются на некоторых специфических особенностях структур определенного вида, используя из как качество исследования систем или разрабатывая ни их основе с применением других методов формализованного представления систем (теоретико-множественных, лингвистических и т.п.) специфические подходы к моделированию.
Структурно-системные модели включают:
методы сетевого моделирования;
сочетание методов структуризации с лингвистическими (языковыми);
структурный подход в направлении формализации построения и исследования структур различного типа (иерархических, матричных, произвольных графов) на основе теоретико-множественных представлений и понятия номинальной шкалы теории измерений.
Ситуационные модели основаны на модельной теории мышления, в рамках которой можно описать основные механизмы регулирования процессов принятия решений. В основе модельной теории мышления лежит представление о формировании в структурах мозга информационной модели объекта и внешнего мира. Эта информация воспринимается человеком на базе уже имеющихся у него знаний и опыта. Целесообразное поведение человека строится путем формирования целевой ситуации и мысленного преобразования исходной ситуации в целевую. Основой построения модели является описание объекта в виде совокупности элементов, связанных между собой определенными отношениями, отображающими семантику предметной области. Модель объекта имеет многоуровневую структуру и представляет собой тот информационный контекст, на фоне которого протекают процессы управления. Чем богаче информационная модель объекта и выше возможности ее манипулирования, тем лучше и многообразнее качество принимаемых решений при управлении.
При реальном моделировании используется возможность исследования характеристик либо на реальном объекте целиком, либо на его части. Такие исследования проводятся как на объектах, работающих в нормальных режимах, так и при организации специальных режимов для оценки интересующих исследователя характеристик (при других значениях переменных и параметров, в другом масштабе времени и т.д.). Реальное моделирование является наиболее адекватным, но его возможности ограничены. Например, проведение реального моделирования АСУП требует, во-первых, наличия такой АСУ и, во – вторых, проведения экспериментов с управляемым объектом, т.е. предприятием, что в большинстве случаев невозможно.
Натурные модели используют при проведении исследования на реальном объекте с последующей обработкой результатов эксперимента на основе теории подобия. Натурный эксперимент подразделяется на научный эксперимент, комплексные испытания и производственный эксперимент. Научный эксперимент характеризуется широким использованием средств автоматизации проведения, применением весьма разнообразных средств обработки информации, возможностью вмешательства человека в процесс проведения эксперимента. В соответствии с этим появилось новое научное направление – автоматизация научного эксперимента и новая специализация в рамках специальности АСУ – АСНИ (автоматизированные системы научных исследований и комплексных испытаний). Одна из разновидностей эксперимента – комплексные испытания, когда вследствие повторения испытаний объектов в целом (или больших частей системы) выявляются общие закономерности о характеристиках качества, надежности этих объектов. В этом случае моделирование осуществляется путем обработки и обобщения сведений о группе однородных явлений. Наряду со специально организованными испытаниями возможна реализация натурного моделирования путем обобщения опыта, накопленного в ходе производственного процесса т.е. можно говорить о производственном эксперименте. Здесь на базе теории подобия обрабатывают статистический материал по производственному процессу и получают его обобщенные характеристики. Необходимо помнить про отличе эксперимента от реального протекания процесса. Оно заключается в том, что в эксперименте могут появиться отдельные критические ситуации и определиться границы устойчивости процесса. В ходе эксперимента вводятся новые факторы и возмущающие воздействия в процесс функционирования объекта.
Другим видом реальных моделей являются физические модели, отличающиеся от натурного тем, что исследование проводится на установказ, которые сохраняют природу явлений и обладают физическим подобием. В процессе физического моделирования задаются некоторые характеристики внешней среды и исследуется поведение либо реального объекта, либо его модели при заданных или создаваемых искусственно воздействиях внешней среды. Физическое моделирование может протекать в реальном и нереальном (псевдореальном) масштабах времени или рассматриваться без учёта времени. В последнем случае изучению подлежат так называемые «замороженные» процессы, фиксируемые в некоторый момент времени. Наибольшие сложности и интерес с точки зрения корректности получаемых результатов представляет физическое моделирование в реальном масштабе времени. [32,39].
Понятие «модель» существенно отличается от понятия «закон».
Закон — это
1) внутренняя и необходимая, всеобщая и существенная связь предметов и явлений объективной действительности;
2) прочное, остающееся, повторяющееся, не так часто меняющееся, идентичное в явлении;
3) одна из ступеней познания человеком единства и взаимосвязи явлений.
Идеализм отрицает объективный характер законов природы и общества и утверждающему, что человеческое сознание, или «мировой разум», будто бы диктуют законы окружающему материальному миру. В противоположность идеализму, материализм учит, что законы существуют объективно, т. е. независимо от сознания людей, что они присущи самой природе и что люди не могут по своему желанию создавать какие-то новые законы или прекращать действие тех или иных законов. Законы тем отличаются от явлений, что они отражают природу, говоря словами Ленина, «глубже, вернее полнее» [22].
Но поскольку закон выражает всеобщие и существенные отношения и связи и отвлекается от частностей и случайностей, постольку он беднее явления модели, а «явление богаче закона». Законы мышления отражают законы материального бытия. Понятие закона примыкает к понятию сущности. По И.В. Ленин: «закон и сущность понятия однородные (однопорядковые) или вернее, одностепенные, выражающие углубление познания человеком явлений, мира» [12,21].
Диалектический материализм исходит из того, что законы носят объективный характер, выражая реальные отношения вещей, а также между свойствами внутри вещи. Существуют законы функционирования, выражающие существенную, необходимую связь между сосуществующими в пространстве вещами и явлениями (например, закон всемирного тяготения). Наряду и в единстве с законами функционирования существуют законы развития. Так, например, общество закономерно развивается от одной общественно-экономической формации к другой.
Законы могут быть менее общими, действующими в ограниченной области и изучаемыми отдельными конкретными науками (например, закон естественного отбора); более общими, изучаемыми рядом областей знания (например., закон сохранения энергии, циркуляции информации); всеобщими, универсальными (законы диалектики: переход количественных изменений в качественные и др.), которые исследуются философией.
Одни законы выражают строгую количественную зависимость между явлениями и фиксируются в науке математическими формулами, другие законы не поддаются математическому выражению. Различают также вероятностные, статистические, статические и динамические закономерности.
Реализация законов зависит от соответствующих необходимых условий, наличие которых обеспечивает переход следствий, вытекающих из законов, из состояния возможности в действительность. В природе законы действуют как стихийная сила. Общественно-исторические законы, есть законы самой человеческой деятельности: они создаются и реализуются людьми в процессе общественной практики. Но действие общественных законов, так же, как и законов природы, объективно. В области мышления всеобщие законы изучают диалектическая логика, частные законы – формальная логика.
На основании познания законов достигается предвидение будущего, осуществляется претворение теории в практику. Посредством познанных законов оказывается возможным управление как природными, так и социальными процессами.
Аксиома (греч. axioma — значимое, достойное уважения, принятое, бесспорное) — истинное суждение (предложение), которое при дедуктивном построении какой-либо теории, в рамках замкнутой теории принимается без доказательства в качестве сходного положения и которое кладется в основу доказательства всех других положений этой теории. В других случаях в качестве аксиом, как правило, выставляют такие положения конструируемой теории, которые несомненно истинны, но не исключены и такие ситуации, когда избранные положения могут в пределах рассматриваемой теории считаться истинными.
Но из этого нельзя сделать вывод, что принятая в данной содержательной теории аксиома вообще введена в теорию без какого-либо первичного обоснования.
Практика показывает, что в содержательных аксиоматически построенных математических теориях обоснование аксиом осуществляется обычно за пределами этих теорий. Аксиоматически построенная формальная система оказывается правомерной и полезной, если она получает интерпретацию, т.е. содержательным подтверждением её (от лат. interpretatio – толкование, разъяснение).
Системе аксиом должны быть присущи следующие качества: непротиворечивость, а также иногда полнота и независимость.
Термин «аксиома» применялся уже Аристотелем (384—322 до н. э.) в смысле истинного предложения или начала, не нуждающегося в доказательстве в силу фактической ясности или методологической простоты. Впоследствии ясность и простота ошибочно истолковываются рядом авторов как очевидность или наглядность. Древнегреческий математик, автор знаменитых «Начал» Евклид (III в. до н. э.) исходил из того, что такие понятия, как «точка» и «прямая», по крайней мере интуитивно ясны каждому, а аксиомы, говорящие об этих геометрических терминах, являются самоочевидными истинами. Такое понимание аксиомы господствовало в течение многих веков. Только в середине XIX в. такая интерпретация этого понятия начала подвергаться критике. Неудовлетворительность такого определения аксиомы заключается в том, что требование «очевидности» носит субъективный характер, так как то, что одному кажется очевидным, для другого — очевидным не является.
Существовало также мнение, будто аксиомы являются абсолютно неизменными, навсегда законченными, непреложными и абсолютно завершенными истинами. В действительности системы аксиом изменяются, совершенствуются в процессе исторического развития познания. Это ярко подтвердило построение Н. И. Лобачевским неевклидовой геометрии, исходя из системы аксиом, коренным образом отличающейся от евклидовой системы аксиом. Более того, аксиоматические системы, описывающие одни и те же совокупности объектов, могут строиться по-разному. В качестве аксиом в одной системе могут приниматься одни предложения, в другой — другие.
Слово «аксиома» очень часто в языке используется и для обозначения суждения, многократно проверенного на практике [12].
Аксиоматический метод - это способ построения научной теории, при котором в её основу кладутся некоторые исходные положения (суждения) — аксиомы, или постулаты, из которых все остальные утверждения этой теории должны выводиться чисто логическим путём, посредством доказательств. Построение науки на основе аксиоматического метода обычно называется дедуктивным. Все понятия дедуктивной теории (кроме фиксированного числа первоначальных) вводятся посредством определений, выражающих их через ранее введённые понятия. В той или иной мере дедуктивные доказательства, характерные для аксиоматического метода, применяются во многих науках, однако главная область его приложения — математика, логика, а также некоторые разделы физики.
Идея аксиоматического метода впервые была высказана в связи с построением геометрии в Древней Греции (Пифагор, Платон, Аристотель, Евклид). Для современной стадии развития аксиоматических методов характерна выдвинутая Д. Гильбертом (1862 - 1943) концепция формального аксиоматического метода, которая ставит задачу точного описания логического средств вывода теорем из аксиом. Основная идея Д. Гильберта — полная формализация языка науки, при которой её суждения рассматриваются как последовательности знаков (формулы), приобретающие смысл лишь при некоторой конкретной интерпретации. Для вывода теорем из аксиом (и вообще одних формул из других) формулируются специальные правила вывода. Доказательство в такой теории (исчислении, или формальной системе) — это некоторая последовательность формул, каждая из которых либо есть аксиома, либо получается из предыдущих формул последовательности по какому-либо правилу вывода. В отличие от таких формальных доказательств, свойства самой формальной системы в целом изучаются содержательными средствами метатеории. Основные требования, предъявляемые к аксиоматическим формальным системам, - непротиворечивость, полнота, независимость аксиом.
Критерием истинности аксиом в содержательных теориях является в конечном счете практическая применимость теории в целом [48].
Постулат (лат. postulatum — требуемое) — это исходное положение, утверждение, принимаемое без строгого доказательства в рамках какой-либо дедуктивно построенной теории, но веское и обоснованное. Отличие постулата от аксиом недостаточно ясно, поэтому они часто отождествляются [12].
Таковы, например, галилеевский принцип относительности и принцип постоянства скорости света в релятивистской механике. Постулаты — это нелогические (специальные) аксиомы теории; их сочетание с аксиомами и правилами логики позволяет описать (индивидуализировать) объекты универсума теории и их свойства.
Постулаты теории выступают как её основные абстракции и служат содержательным, основанием для вывода других её положений-теорем. Подобное толкование постулата согласуется с античной традицией, восходящей к «Началам» Евклида. Иногда под постулатами (или правилами преобразования) подразумевают все аксиомы, схемы аксиом, определения и правила вывода рассматриваемой формальной системы. Встречается также толкование постулатов как спорных положений, включение которых в число исходных принципов (аксиом) не приводит, однако, к противоречию. В этом смысле постулат будет, например, по отношению к другим аксиомам логики — исключённого третьего [48]






